【算法分析与设计】盛更多的水
发布时间:2024年01月10日
题目
给定一个长度为?
n?的整数数组?height?。有?n?条垂线,第?i?条线的两个端点是?(i, 0)?和?(i, height[i])?。找出其中的两条线,使得它们与?
x?轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例:
示例 1:
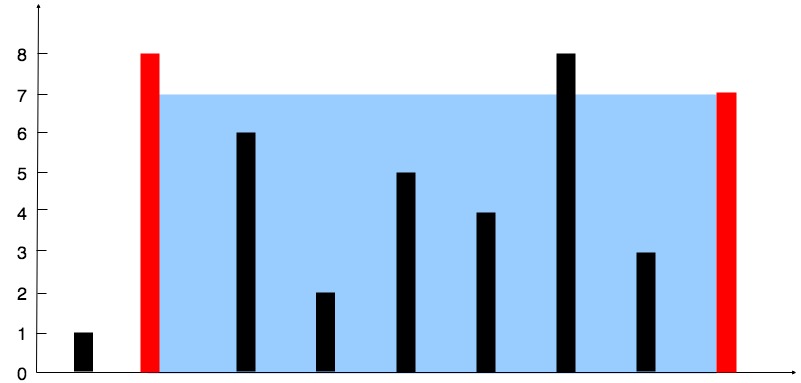
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为?49。示例 2:
输入:height = [1,1] 输出:1
思路
直接思路:暴力破解
利用两层for循环来遍历所有情况,时间复杂度是n;
抱着侥幸心理试试,万一过了呢
代码实现
class Solution {
public int maxArea(int[] height) {
int max=0;
int h;
int w;
int s;
for(int i=0;i<height.length;i++){
for(int j=i+1;j<height.length;j++){
h=Math.min(height[i],height[j]);
w=j-i;
s=w*h;
if(s>max){
max=s;
}
}
}
return max;
}
}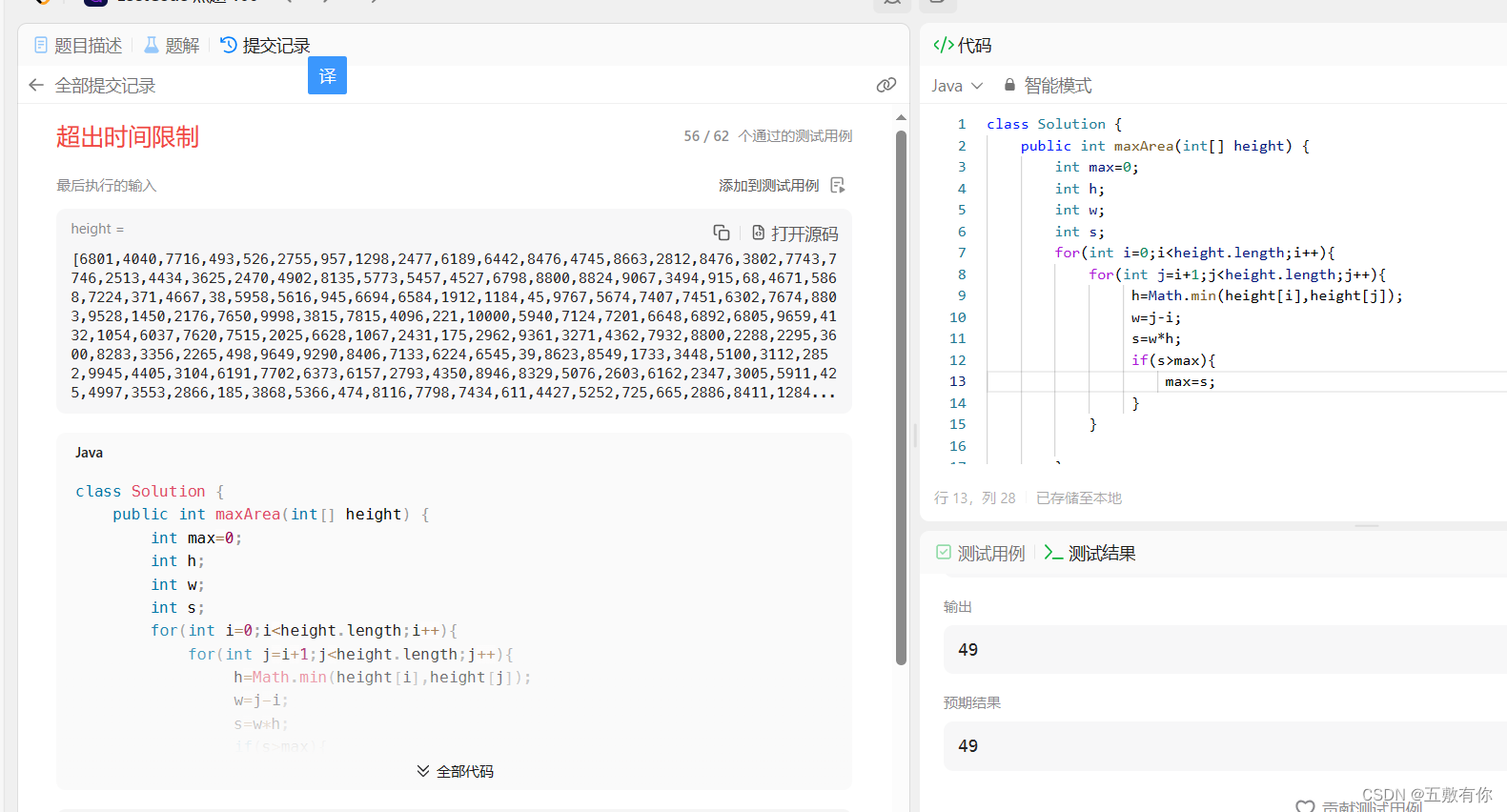
?不出意料,失败了。。。
思路二
分支,迭代都不行,看了题解才直到双指针。
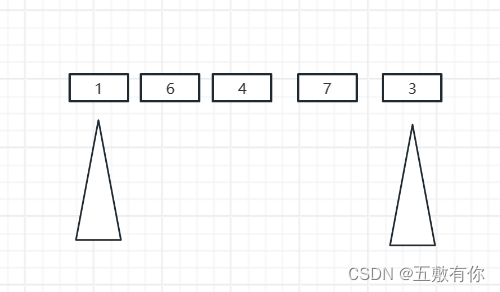
这个双指针开始是在最左和最右边的,那边矮就那边向中间靠近。
可能有人不理解会不会丢失情况。
这个大可放心,因为最开始宽是最大的,向中间移动就是宽度在缩小,而max只能是高度战胜它,所以不会丢失情况。只是遍历一遍所以时间复杂度是o(n)
class Solution {
public int maxArea(int[] height) {
int max=0;
int h;
int w;
int s;
int left=0;
int right=height.length-1;
while(left<right){
h=Math.min(height[left],height[right]);
w=right-left;
s=w*h;
if(s>max){
max=s;
}
if(height[left]<height[right]){
left++;
}else{
right--;
}
}
return max;
}
}通过!!!?

文章来源:https://blog.csdn.net/m0_62645012/article/details/135498567
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- YOLOv8添加加权双向金字塔结构的特征加强模块BiFPN
- 寒假计划(待定)
- LeetCode Hot100 295.数据流的中位数
- 裸色打底裤:“光腿神器”怎么就成了“美丽刑具”?
- RDD算子——Action 操作
- 力扣第 379 场周赛VP
- Vue入门三(表单控制|购物车案例|v-model进阶|与后端交互)
- Golang学习之路一开山篇
- ubuntu桥接方式上网
- Bearer +token是必需的吗,uniapp项目中,是不需要Bearer的,加了会报错,报500服务器问题