德思特干货丨如何使用SBench6软件对数字化仪采集信号进行处理？（一）——波形算术运算与直方图功能

来源：德思特测量测试 德思特干货丨如何使用SBench6软件对数字化仪采集信号进行处理？（一）——波形算术运算与直方图功能

原文链接：https://mp.weixin.qq.com/s/whJUKFsskQbr5DXzBE4hfA

欢迎关注虹科，为您提供最新资讯！

1?前言

板卡式数字化仪可以实现准确、高分辨率的数据采集，并能快速传输到计算机主机。在计算机主机中应用的信号处理程序，可以帮助用户获得更多的数据，或从简单的测量中提取出极为有用的信息。

现代板卡式数字化仪，会有一系列软件为其提供功能增强支持。比如德思特SBench 6和许多第三方程序，都包含多种信号处理功能。这些功能包括波形算术运算、分组和滑动平均、快速傅立叶变换（FFT）、高级滤波功能和直方图。本文将展开介绍上述这些功能，并提供这些处理工具的典型应用示例。

2?模拟量运算（波形算术运算）

模拟量运算包括对获取到的波形进行加减乘除四则运算。这些应用于波形的运算可以改善信号质量，或推导出其它更多有用的信息。其中一例子是使用减法运算，将差分信号组合成具有更低共模噪声和拾取水平的差分波形。而另一个例子则是将电流和电压波形进行乘积，计算瞬时功率曲线。

所有这些算术函数都应用于波形的上的每一个采样点数据。首先，我们假设要合成的波形具有相同的采样点长度。我们按照图1显示的路径，在SBench 6软件中找到“Analog Calculation（模拟运算）”设置项的位置。

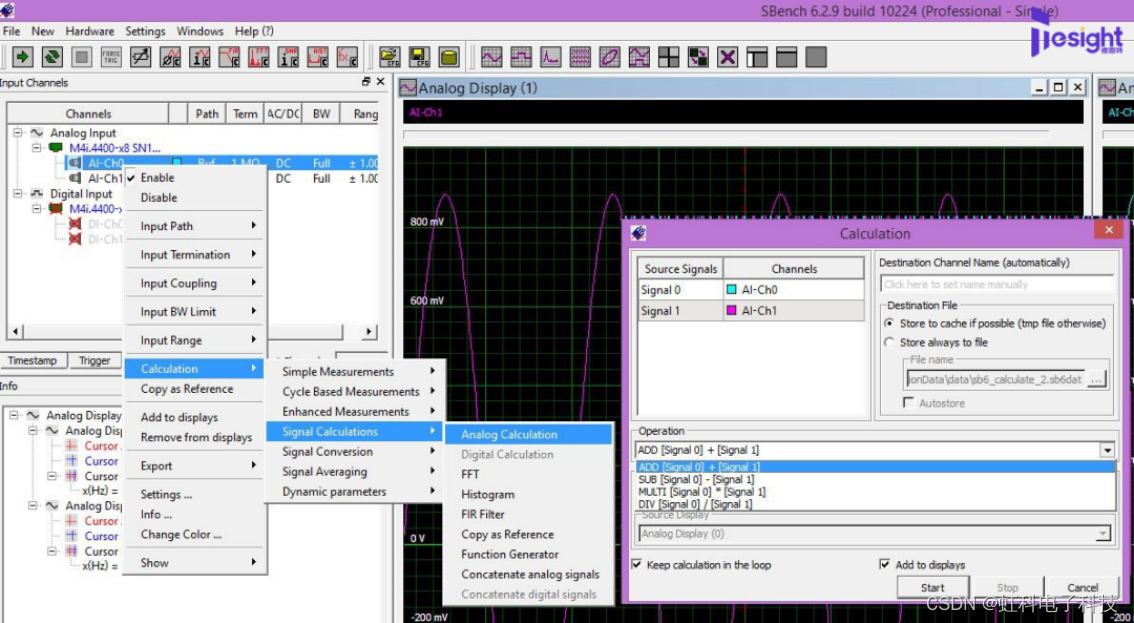
图1：SBench 6中针对每个信号的运算处理选项

右键单击需要参与运算的原始通道，在弹出的选择框中选择“Simple Measurements（采样点测量）”、“Signal Calculations（信号计算）”、“Signal Conversion（信号转换）”和“Signal Averaging（信号平均）”会展示额外的选项。例如，信号计算选择提供了模拟运算、快速傅立叶变换（FFT）、直方图、滤波和其他几种函数运算。如果选择了模拟预算，运算对话框会弹出，允许设置所需的算术运算。在图中例子中，AI-Ch0和AI-Ch1两个原始信号将被相加。其他选项包括减法（SUB）、乘法（MULTI）和除法（DIV）。其他刚才提到的信号处理函数也可以用类似的方式进行选择和设置。

接下来，我们会展示将波形算术运算应用于实际问题的第一个示例，那就是将一个信号组件从另一个信号中减去，以计算差分信号，如图2所示。

图2：使用减法功能，从两个差分通道信号中得出差分信号

差分技术通常用于改善信号的完整性。在图2所示的示例中，1 MHz时钟的“P”和“N”成分（在两个右侧窗格中显示）使用减法运算进行合并。得到的差分信号在中间窗格中显示。而左侧中部的“Info”窗格，则使用峰峰值和平均值两个指标对每个波形进行了测量。我们很容易看出，差分信号的峰峰值接近原来的两倍，并且平均值接近零。此外，差分成分中的共模噪声已被消除。

第二个示例是将电压波形与电流波形相乘，以获得如图3所示的瞬时功率。

图3：使用乘法函数从开关电源的电流及电压波形计出算瞬时功率

原始波形是功率场效应晶体管（FET）上的电压和在开关电源的Flyback模式下FET的通过电流。这些波形的乘积表示FET瞬时消耗的功率。电流波形（右上窗格）在FET导通期间线性增加，峰值约为600 mA。FET上的电压在导通期间则最小，但在关断时升至260V的峰值。这两个波形的乘积在左侧窗格中显示，这就是瞬时功率波形。波形体现了在导通和关断状态之间的转换时出现显著的功率尖峰。而平均值（5.111 W）和峰值功率（44.25 W）则显示在左侧中部的“Info”窗格中。

这些示例展现了使用模拟运算从原始波形中获取出其他重要的波形的能力和方法。

3?直方图

我们还可以在统计域中查看数据。这通常用于获知某些幅度值发生的概率，而实现的方式则是绘制波形幅值与其出现频次的直方图。所得的直方图就是信号概率分布的有限记录长度估计。在德思特SBench 6软件中，我们提供了创建已获取波形直方图的能力。图4中显示了一系列示例，包括正弦波，三角波和噪声波形以及它们对应的直方图分布。

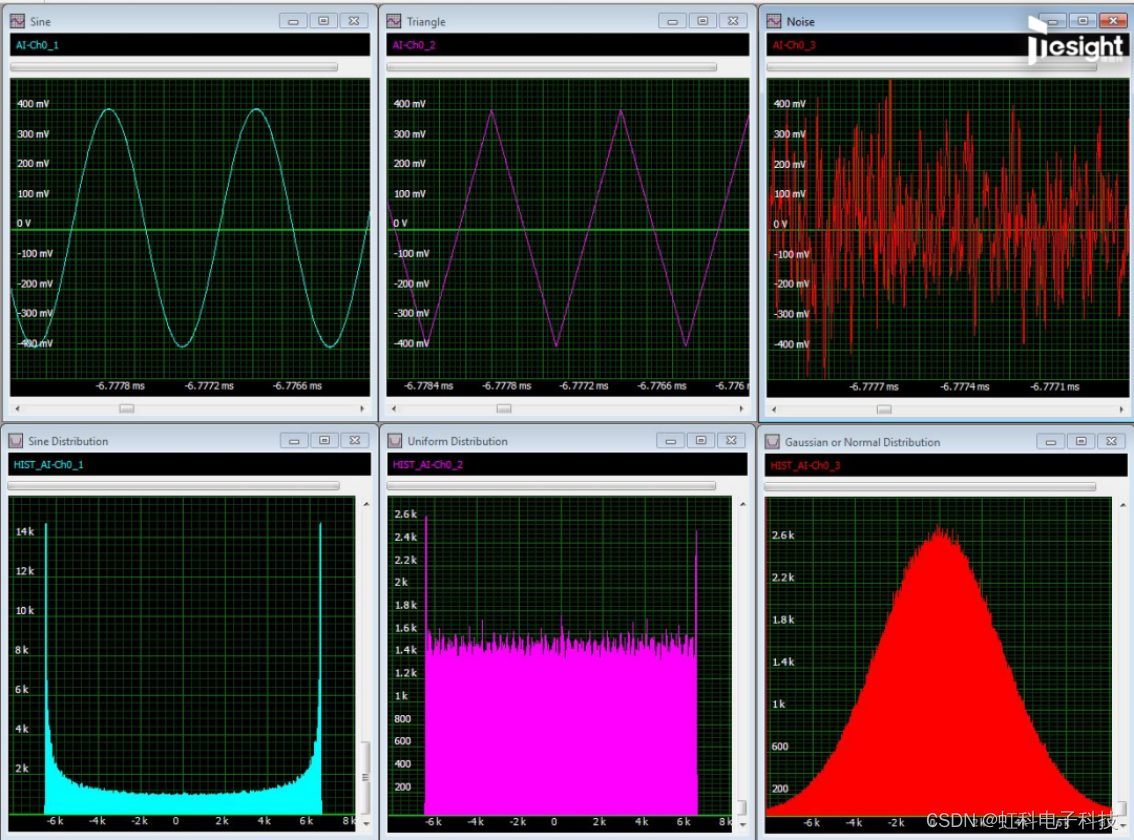
图4：一些常见波形示例，以及它们对应的直方图

上面一行窗格显示了正弦波、三角波和噪声波的原始波形，下面一行则是对应的直方图。其中，直方图的水平轴表示信号的幅度。垂直轴显示在小范围内（分组）的值的数量。

每个波形的直方图分布都是独特的，差异与信号本身的特性有关。正弦波的直方图分布显示在两端上有高峰，而中部呈鞍形。形成这种形状的原因是正弦波的幅值在整个周期内都在变化，且变化率（导数）在零交点处最高，在峰值处最低。如果将正弦波以均匀的时间间隔切割成小片段，那么在正峰值（直方图的最右侧峰值）和负峰值（直方图的最左侧峰值）处会有更多的样本片段，在零交点（在直方图的水平中心）处样本最少。

三角波则具有恒定的斜率绝对值，只是斜率正负在发生变化。结果就是其直方图具有均匀的分布，除了在两侧最极端处。峰值存在是因为信号发生器具有有限的带宽，这会使得峰值波形变圆，从而使得在这一段上获取的样本更多。

众所周知，噪声信号的直方图一般呈现高斯或正态分布，其原因不再赘述。高斯分布的特征在于它没有边界。其他分布一般有幅度限制，水平范围是固定的。而高斯分布有很长的“尾部”，理论上是可以向两侧延伸到无穷大的，但在实际仪器操作中，其“尾部”会被数字化仪的采集电平范围所限制。

因此，直方图也能一定程度上反映信号的问题。它们尤其适用于显示波形的不对称性（失真）和小概率发生瑕疵。图5展示了一个带有过零失真的正弦波信号对应的直方图。

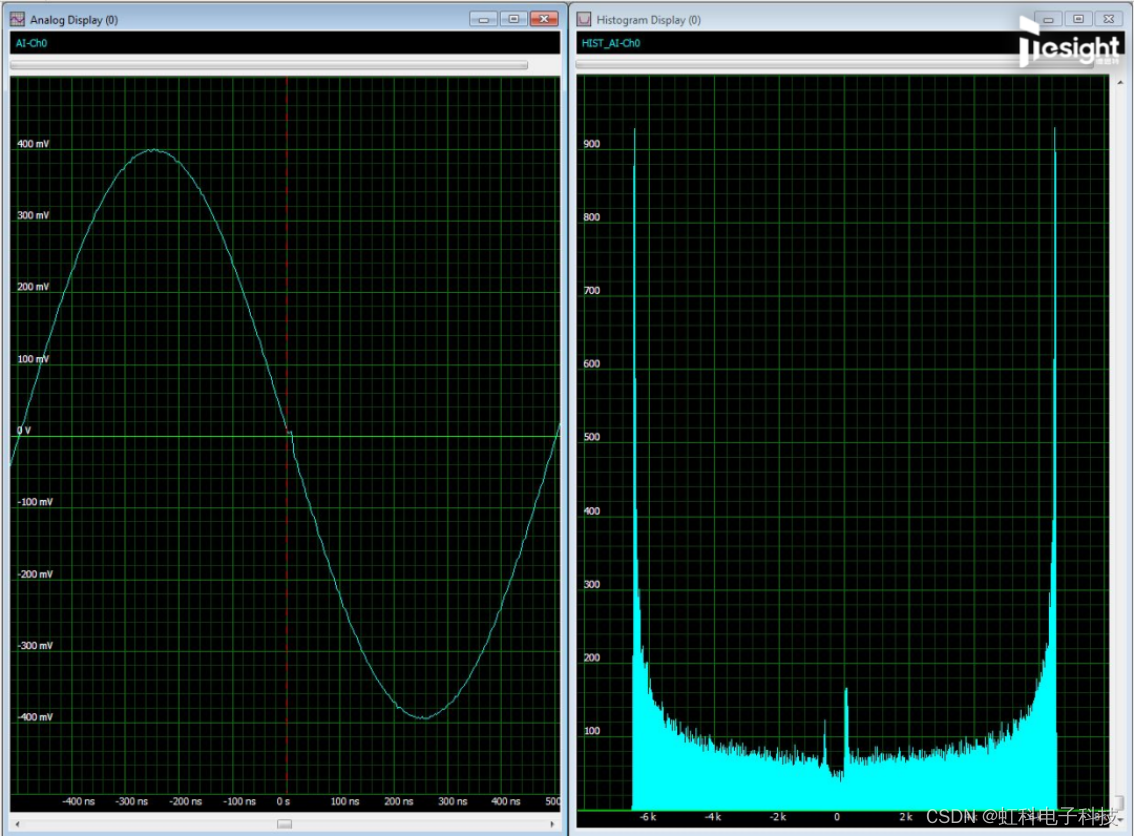
图5：带有过零失真的正弦波信号，及其对应的直方图