【数学建模】《实战数学建模：例题与讲解》第十三讲-相关分析（含Matlab代码）

本系列侧重于例题实战与讲解，希望能够在例题中理解相应技巧。文章开头相关基础知识只是进行简单回顾，读者可以搭配课本或其他博客了解相应章节，然后进入本文正文例题实战，效果更佳。

如果这篇文章对你有帮助，欢迎点赞与收藏~

基本概念

1. 变量类型：在进行相关分析之前，首先要确定所研究的变量类型。这些变量可以是连续的（如身高、体重）或者离散的（如性别、婚姻状况）。
2. 相关系数：相关分析的核心是计算相关系数，这是一个度量值，表明两个变量之间的关系有多紧密。最常用的相关系数是皮尔逊相关系数（Pearson correlation coefficient），用于度量两个连续变量之间的线性关系。
3. 线性与非线性关系：皮尔逊相关系数主要用于评估线性关系。对于非线性关系，可能需要使用其他类型的相关系数，如斯皮尔曼等级相关系数（Spearman’s rank correlation coefficient）。
4. 方向：相关系数的值范围通常在-1到+1之间。一个正的相关系数意味着一个变量增加时，另一个变量也增加；负的相关系数则意味着一个变量增加时，另一个变量减少。
5. 统计显著性：仅仅计算出相关系数是不够的，还需要评估这种相关性是否具有统计显著性。通常，这通过进行假设检验（如t检验）来实现。
6. 因果关系：值得注意的是，即使两个变量之间存在强相关性，也不能自动推断出因果关系。相关性只能揭示变量之间的关联，而不是因果。

本文中的相关知识：

典型相关分析

计算两组变量（表示为 X 组和 Y 组）的典型变量，这些典型变量是通过线性组合构成，目的是最大化两组变量间的相关性。
计算原始变量与典型变量之间的相关系数，这展示了原始变量与新构造的典型变量之间的关联强度。
分析典型变量之间的典型相关系数，这反映了两组变量间的整体关联强度。

综合评价模型

用于评估多个指标的综合影响。在这个例子中，使用了无量纲化方法来处理不同单位或量级的数据，使得比较和评估成为可能。
使用欧氏距离和绝对值距离来评估不同湖泊水质的富营养化等级。

对应分析

这是一种用于探索分类数据的多元统计技术，它可以揭示分类变量之间的关系。在这个例子中，通过对应分析可以看出不同地区和指标之间的关系。

因子分析

用于数据简化和变量归约。在这个例子中，通过因子分析将多个变量简化为少数几个因子，从而使得解释变得更加简洁。

聚类分析

包括 R 型和 Q 型聚类，分别用于变量和样本点的分类。通过聚类分析，可以将变量或样本点分为不同的组，从而发现数据的内在结构。

习题10.4

1. 题目要求

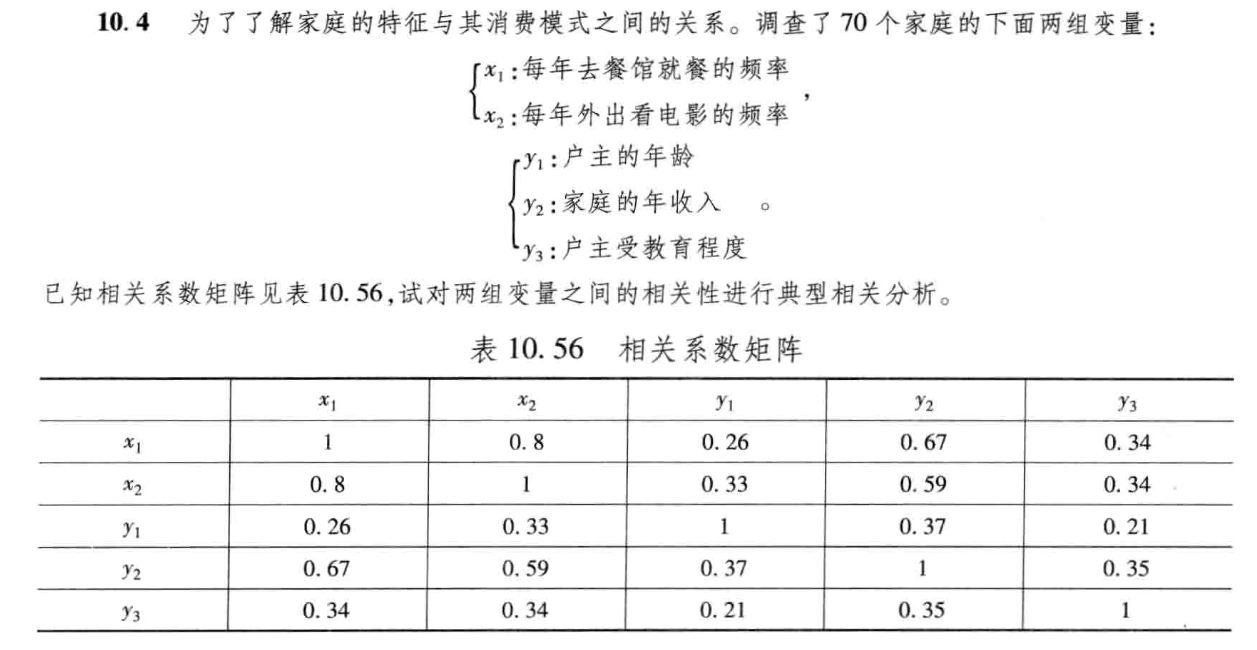
2.解题过程

解：

1. 根据计算，我们得到了 $\mathbf{X}$ 组的典型变量为：
   $$u_1=0.7689x_1+0.2721x_2$$

   $$u_2=?1.4787x_1+1.6443x_2$$

2. 我们也得到了原始变量与 $\mathbf{X}$ 组典型变量之间的相关系数（如表 1）、原始变量与 $\mathbf{Y}$ 组典型变量之间的相关系数（如表 2），以及两组典型变量之间的典型相关系数（如表 3）。

   表 1：原始变量与 X 组典型变量之间的相关系数

   	$x_1$	$x_2$	$y_1$	$y_2$	$y_3$
   $u_1$	0.986586	0.887215	0.289705	0.675704	0.35394
   $u_2$	-0.16324	0.461356	0.158162	-0.02058	0.05631

   表 2：原始变量与 Y 组典型变量之间的相关系数

   	$x_1$	$x_2$	$y_1$	$y_2$	$y_3$
   $v_1$	0.67872	0.610358	0.421115	0.982203	0.514487
   $v_2$	-0.0305	0.086212	0.846397	-0.11014	0.301341

   表 3：两组典型变量之间的典型相关系数

   1	0.6879
   2	0.1869

   从这些表中，我们可以看到，两个表示外出活动特性的变量 $x_1$ 和 $x_2$ 与 $u_1$ 的相关系数较大，说明 $u_1$ 可以被视为形容外出活动特性的指标。在第一对典型变量中，$v_1$ 与 $y_2$ （代表家庭年收入）的相关系数较大，因此我们可以认为 $v_1$ 主要代表了家庭的年收入。此外，$u_1$ 和 $v_1$ 之间的典型相关系数为 0.6879，说明这两个典型变量在一定程度上是相关的。

3. 最后，对于原始变量的解释度，$u_1$ 和 $v_1$ 解释的本组原始变量的比率分别为 0.8803 和 0.4689。这表示 $u_1$ 和 $v_1$ 在一定程度上能够解释原始变量的变异。而且，$\mathbf{X}$ 组的原始变量被 $u_1$ 和 $u_2$ 完全（100%）解释了，而 $\mathbf{Y}$ 组的原始变量被 $v_1$ 和 $v_2$ 解释了 74.2%，说明典型变量确实能够在很大程度上表现出原始变量的特性。

3.程序

求解的MATLAB程序如下：

clc, clear;

% 加载数据
correlation_matrix = load('data104.txt');

% X组和Y组变量的数量
num_X = 2;
num_Y = 3;
num_min = min(num_X, num_Y);

% 提取X与X，Y与Y，Y与X的相关系数
correlation_XX = correlation_matrix([1:num_X], [1:num_X]);
correlation_YX = correlation_matrix([1:num_X], [num_X+1:end]);
correlation_XY = correlation_YX';
correlation_YY = correlation_matrix([num_X+1:end], [num_X+1:end]);

% 计算矩阵M1和M2
matrix_M1 = inv(correlation_XX) * correlation_YX * inv(correlation_YY) * correlation_XY;
matrix_M2 = inv(correlation_YY) * correlation_XY * inv(correlation_XX) * correlation_YX;

% 求M1的特征向量和特征值
[eigVec_M1, eigVal_M1] = eig(matrix_M1);
for i = 1:num_X
    % 特征向量归一化，满足a's1a=1，特征向量乘±1，保证所有分量和为正
    eigVec_M1(:, i) = eigVec_M1(:, i) / sqrt(eigVec_M1(:, i)' * correlation_XX * eigVec_M1(:, i));
    eigVec_M1(:, i) = eigVec_M1(:, i) / sign(sum(eigVec_M1(:, i)));
end
% 计算特征值的平方根，按照从大到小排列
eigVal_M1 = sqrt(diag(eigVal_M1));
[eigVal_M1, ind1] = sort(eigVal_M1, 'descend');

% 取出X组的系数阵和典型相关系数
coef_X = eigVec_M1(:, ind1(1:num_min));
canCorrelation_X = eigVal_M1(1:num_min);

% 求M2的特征向量和特征值
[eigVec_M2, eigVal_M2] = eig(matrix_M2);
for i = 1:num_Y
    % 特征向量归一化，满足b's2b=1，特征向量乘±1，保证所有分量和为正
    eigVec_M2(:, i) = eigVec_M2(:, i) / sqrt(eigVec_M2(:, i)' * correlation_YY * eigVec_M2(:, i));
    eigVec_M2(:, i) = eigVec_M2(:, i) / sign(sum(eigVec_M2(:, i)));
end
% 计算特征值的平方根，按照从大到小排列
eigVal_M2 = sqrt(diag(eigVal_M2));
[eigVal_M2, ind2] = sort(eigVal_M2, 'descend');

% 取出Y组的系数阵和典型相关系数
coef_Y = eigVec_M2(:, ind2(1:num_min));
canCorrelation_Y = eigVal_M2(1:num_min);

% 计算X，u；Y，v；X，v；Y，u的相关系数
correlation_XU = correlation_XX * coef_X;
correlation_YV = correlation_YY * coef_Y;
correlation_XV = correlation_YX * coef_Y;
correlation_YU = correlation_XY * coef_X;

% 计算X组、Y组原始变量被ui、vi解释的方差比例
ratio_XU = sum(correlation_XU.^2) / num_X;
ratio_XV = sum(correlation_XV.^2) / num_X;
ratio_YU = sum(correlation_YU.^2) / num_Y;
ratio_YV = sum(correlation_YV.^2) / num_Y;

% 输出结果
fprintf('X组的原始变量被u1~u%d解释的比例为%f\n', num_min, sum(ratio_XU));
fprintf('Y组的原始变量被v1~v%d解释的比例为%f\n', num_min, sum(ratio_YV));

习题10.5

1. 题目要求

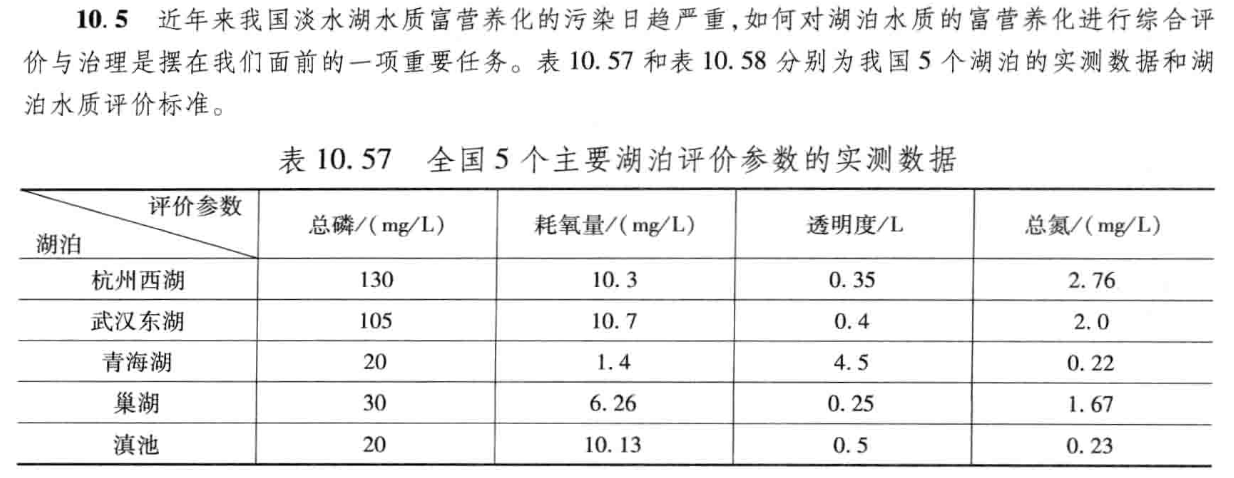
2.解题过程

解：

在进行综合评价之前，首先要对评价的指标进行分析。通常的评价指标分为效益型、成本型和固定型指标。效益型指标是指那些数值越大影响力越大的统计指标(也称为正向型指标);成本型指标是指数值越小越好的指标(亦称为逆向型指标);而固定型指标是指数值越接近某个常数越好的指标(又称为适度型指标)。如果各评价指标的属性不一致,则在进行综合评估时容易发生偏差,必须先对各评价指标统一属性。

1. 建立无量纲化实测数据矩阵和评价标准矩阵。实测数据矩阵为 $\mathbf{A}$ 和等级标准矩阵为 $\mathbf{B}$，然后建立无量纲化实测数据矩阵 $\mathbf{C}$ 和无量纲化等级标准矩阵 $\mathbf{D}$。其中，$c_{ij}$ 和 $d_{kt}$ 的计算方法如下：

   $c_{ij}$ 和 $d_{kt}$ 的计算方式：
   $$c_{ij}=\{\begin{array}{ll}{a}_{ij}/{\max }_i{a}_{ij},& \text{if?}j\ne 3\\ {\min }_i{a}_{ij}/a_{ij},& \text{if?}j=3\end{array}$$

   $$d_{kt}=\{\begin{array}{ll}{b}_{kt}/{\max }_i{b}_{kt},& \text{if?}k\ne 3\\ {\min }_i{b}_{kt}/b_{kt},& \text{if?}k=3\end{array}$$

2. 计算 $\mathbf{D}$ 的各行向量的均值 ${\mu }_i$、标准差 $s_i$ 和变异系数 $w_i$，以及权向量 $\mathbf{w}$。计算公式如下：

   ${\mu }_i$，$s_i$ 和 $w_i$ 的计算方式：
   $${\mu }_i=0.2\sum _{j=1}^5{d}_{ij}{s}_i=\sqrt{\frac{{\sum }_{j=1}^5(d_{ij}?{\mu }_i{)}^2}{4}}{w}_i=s_i/{\mu }_i$$

   $\mathbf{w}$ 的计算方式：
   $$\mathbf{w}=[0.277,0.2447,0.2347,0.2442]$$

3. 建立综合评价模型，计算 $\mathbf{C}$ 中各个行向量到 $\mathbf{D}$ 中各个列向量的欧氏距离 $x_{ij}$ 和绝对值距离 $y_{ij}$。若 $x_{ik}={\min }_{1\le j\le 5}{x}_{ij}$ 或 $y_{ik}={\min }_{1\le j\le 5}{y}_{ij}$ 则表明第 $i$ 个湖泊属于第 $k$ 级。

   然后，我们可以得到以下欧氏距离判别表和绝对值距离判别表。$x_{ij}$ 和 $y_{ij}$ 的计算方式：
   $$\begin{gathered} x_{ij}=\sqrt{\sum _{k=1}^4(c_{ik}?d_{kj}{)}^2} \\ {y}_{ij}=\sum _{k=1}^4|c_{ik}?d_{kj}| \end{gathered}$$

然后，我们可以得到以下欧氏距离判别表和绝对值距离判别表。

欧氏距离判别表

湖泊	$x_{i1}$	$x_{i2}$	$x_{i3}$	$x_{i4}$	$x_{i5}$	级别
杭州西湖	1.8472	1.8312	1.7374	1.3769	0.2881	5
武汉东湖	1.5959	1.5798	1.4859	1.1271	0.5034	5
青海湖	0.2185	0.2045	0.1367	0.3383	1.7917	3
巢湖	1.3201	1.3038	1.2082	0.8392	0.9591	4
滇池	1.0793	1.0650	0.9867	0.7328	1.3450	4

绝对值距离判别表

湖泊	$y_{i1}$	$y_{i2}$	$y_{i3}$	$y_{i4}$	$y_{i5}$	级别
杭州西湖	3.6631	3.6303	3.4374	2.6783	0.3231	5
武汉东湖	3.1436	3.1108	2.9178	2.1587	0.8427	5
青海湖	0.4062	0.3734	0.2110	0.5787	3.5800	3
巢湖	2.4071	2.3743	2.1814	1.4223	1.5791	4
滇池	1.6701	1.6374	1.4444	1.0660	2.3161	4

从上面的计算可知，尽管欧几里得距离与绝对值距离意义不同，但是对各湖泊水质的富营养化的评价等级是一样的，表明此处给出的方法具有稳定性。

3.程序

求解的MATLAB程序如下：

% 清除环境变量
clc; clear;

% 初始化实测数据矩阵
rawData = [130,10.3,0.35,2.76;
    105,10.7,0.4,2.0;
    20,1.4,4.5,0.22;
    30,6.26,0.25,1.67;
    20,10.13,0.5,0.23];

% 初始化等级标准矩阵
standardMatrix = [1,4,23,110,660;
    0.09,0.36,1.8,7.1,27.1;
    37,12.,2.4,0.55,0.17;
    0.02,0.06,0.31,1.2,4.6];

% 进行无量纲化处理
normalizedRawData = rawData ./ repmat(max(rawData), size(rawData, 1), 1);
normalizedRawData(:, 3) = min(rawData(:, 3)) ./ rawData(:, 3);

normalizedStandardMatrix = standardMatrix ./ repmat(max(standardMatrix, [], 2), 1, size(standardMatrix, 2));
normalizedStandardMatrix(3, :) = min(standardMatrix(3, :)) ./ standardMatrix(3, :);

% 计算均值和标准差
average = mean(standardMatrix, 2);
standardDeviation = std(standardMatrix, [], 2);

% 计算权重
weights = standardDeviation ./ average;
weights = weights / sum(weights);

% 计算欧式距离
euclideanDistances = dist(normalizedRawData, normalizedStandardMatrix);

% 计算绝对值距离
absoluteDistances = mandist(normalizedRawData, normalizedStandardMatrix);

习题10.6（1）

1. 题目要求

2.解题过程——对应分析

解：

分别用 $i=1,\dots ,16$ 表示，以 $a_{ij}$ 表示第 i 个地区第 j 个指标变量 $x_j$ 的取值。

记：
$$\mathbf{A}=(a_{ij}{)}_{16\times 6}$$
记：
$$a_{i?}=\sum _{j=1}^6{a}_{ij},a_{?j}=\sum _{i=1}^{16}{a}_{ij}$$
首先把 $\mathbf{A}$ 化为规格化的“概率”矩阵 $\mathbf{P}$ ， 记 $\mathbf{P}=(p_{ij}{)}_{16\times 6}$ ，其中 $p_{ij}=a_{ij}/\mathbf{T}$ ，$\mathbf{T}={\sum }_{i=1}^{16}{\sum }_{j=1}^6{a}_{ij}$。再对数据进行对应变换，令 $\mathbf{B}=(b_{ij}{)}_{16\times 6}$ ，其中：
$$b_{ij}=\frac{p_{ij}?p_{i?}{p}_{?j}}{\sqrt{p_{i?}{p}_{?j}}}=\frac{a_{ij}?a_{i?}{a}_{?j}/\mathbf{T}}{\sqrt{a_{i?}{a}_{?j}}},i=1,2,\dots ,16,j=1,2,\dots ,6.$$
对 $\mathbf{B}$ 进行奇异值分解，$\mathbf{B}=\mathbf{U}\Lambda {\mathbf{V}}^{\mathbf{T}}$，其中 $\mathbf{U}$ 为 $16\times 16$ 正交矩阵，$\mathbf{V}$为 $6\times 6$ 正交矩阵，$\Lambda =\left[\begin{array}{cc}{\Lambda }_m& 0\\ 0& 0\end{array}\right]$，这里 $ \varLambda_m=diag(d_1,\dots,d_m) $ ，其中 $d_i(i=1,2,\dots ,m)$ 为 $\mathbf{B}$ 的奇异值。

记 $\mathbf{U}=[{\mathbf{U}}_1?{\mathbf{U}}_2],\mathbf{V}=[{\mathbf{V}}_1?{\mathbf{V}}_2]$ ，其中 ${\mathbf{U}}_1$ 为$16\times m$ 的列正交矩阵，${\mathbf{V}}_1$ 为 $6\times m$ 的列正交矩阵，则 $\mathbf{B}$ 的奇异值分解式等价于$\mathbf{B}={\mathbf{U}}_1\Lambda {{\mathbf{V}}_1}^T$。

记 ${\mathbf{D}}_{\mathbf{r}}=diag(p_{1?},p_{2?},\dots ,p_{16?}),{\mathbf{D}}_{\mathbf{c}}=diag(p_{?1},p_{?2},\dots ,p_{?6})$ ，其中 $p_{i?}={\sum }_{j=1}^6{p}_{ij}$ ，$p_{?j}={\sum }_{i=1}^{16}{p}_{ij}$。则列轮廓的坐标为 $\mathbf{F}={\mathbf{D}}_c^{?1/2}{\mathbf{V}}_1{\Lambda }_m$ ，行轮廓的坐标为 $\mathbf{G}={\mathbf{D}}_r^{?1/2}{\mathbf{V}}_1{\Lambda }_m$ 。最后通过贡献率的比较确定需要截取的维数，形成对应分析图。

计算 ${\mathbf{B}}^{\mathbf{T}}\mathbf{B}$ 的特征值，惯量，表示相应维数对各类别的解释量，最大维数 $m=\min 16?1,6?1$ ，本例最多可以产生5个维数。从下表可看出，第一维数的解释量达 77.4% ，前两个维数的解释度已达92.1%。

维数	奇异值	惯量	贡献率	累积贡献率
1	0.189893	0.036059	0.773764	0.773764
2	0.082831	0.006861	0.147224	0.920988
3	0.047138	0.002222	0.047618	0.968669
4	0.03113	0.000969	0.020795	0.989464
5	0.022159	0.000491	0.010536	1

行坐标

	北京	天津	河北	山西	内蒙古	辽宁
第一维	-0.07905	-0.06783	-0.26354	0.457766	0.07715	-0.13567
第二维	-0.0354	0.138818	-0.10045	-0.05715	0.156316	-0.08455

	吉林	黑龙江	上海	江苏	浙江	安徽
第一维	-0.27126	-0.19757	0.386809	0.086955	0.079122	-0.14212
第二维	-0.00074	0.045985	-0.07833	-0.04222	-0.01969	-0.14225

	福建	江西	山东	河南
第一维	-0.17469	-0.18859	0.069823	-0.1462
第二维	-0.11317	-0.1527	0.100318	0.032858

列坐标

	x1	x2	x3	x4	x5	x6
第一维	-0.07905	-0.06783	-0.26354	0.457766	0.07715	-0.13567
第二维	-0.0354	0.138818	-0.10045	-0.05715	0.156316	-0.08455

在下图中，给出16个地区和6个指标在相同坐标系上绘制的散布图。

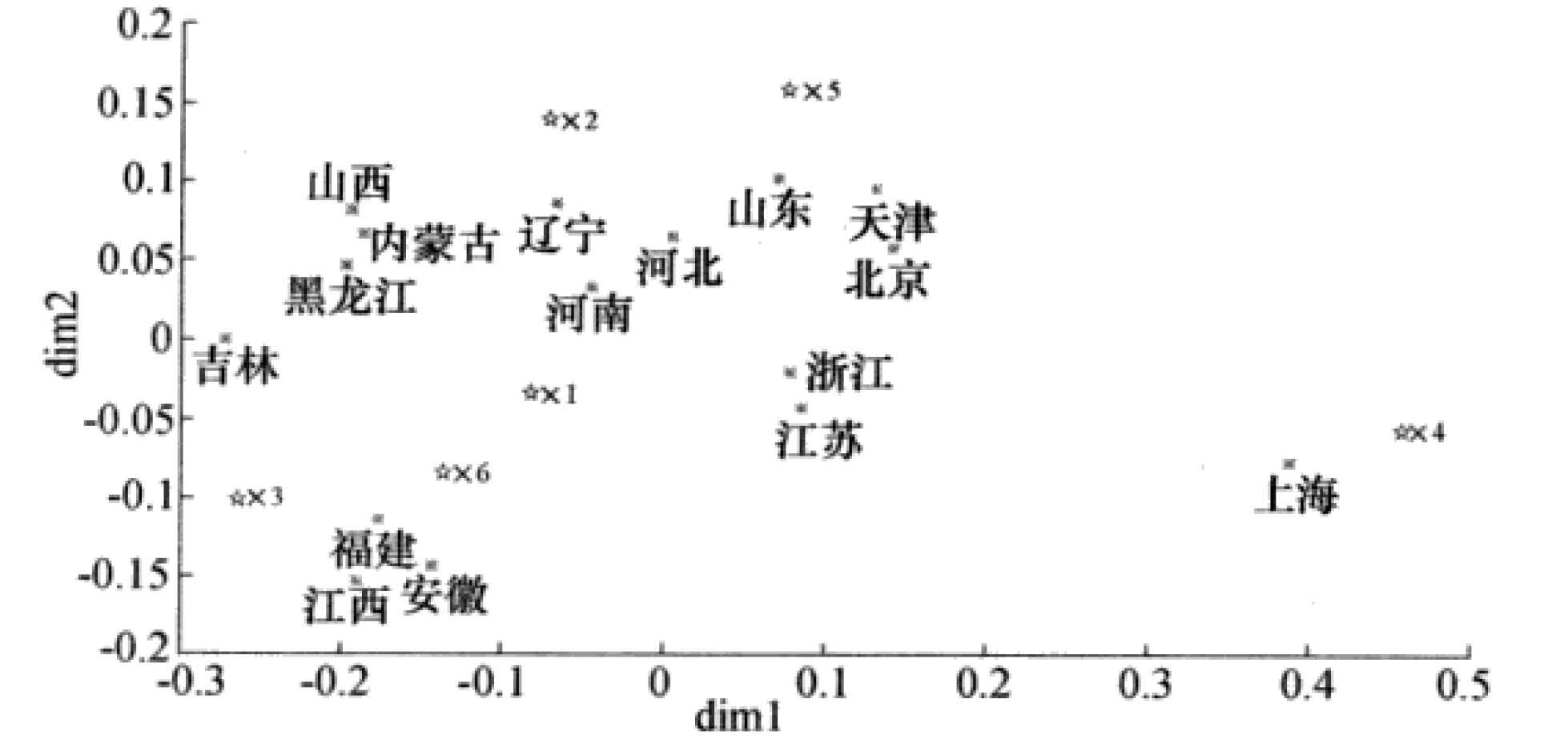
从图中可以看出，地区和指标点可以分为两类，

第一类包括指标点 $x_4,x_5$ ，地区点为北京、天津、河北、上海、江苏、浙江、山东；

第二类包括指标点 $x_1,x_2,x_3,x_6$ ，地区点为其余地区。

3.程序

求解的MATLAB程序如下：

clc, clear

% 原始数据，其中包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
    135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
    95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
    104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
    128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
    145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
    159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
    116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
    221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
    144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
    169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
    153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
    144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
    140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
    115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
    101.18, 23.26, 8.46, 20.20, 20.50, 4.30];

% 计算原始数据的总和
totalSum = sum(sum(originalData));

% 计算原始数据的比例
ratioData = originalData / totalSum;

% 计算行和列的比例
rowRatio = sum(ratioData, 2);
columnRatio = sum(ratioData);

% 计算行剖面数据
Row_prifile = originalData ./ repmat(sum(originalData, 2), 1, size(originalData, 2));

% 计算B（B为对应分析的基础矩阵）
B = (ratioData - rowRatio * columnRatio) ./ sqrt(rowRatio*columnRatio);

% 对B矩阵进行奇异值分解，得到U，S，V矩阵
[U, S, V] = svd(B, 'econ');

% 对V矩阵列求和并根据其符号调整权重
W1 = sign(repmat(sum(V), size(V, 1), 1));

% 对U矩阵列求和并根据其符号调整权重
W2 = sign(repmat(sum(V), size(U, 1), 1));

% 应用权重调整V和U矩阵
V_adjusted = V .* W1;
U_adjusted = U .* W2;

% 计算lambda（特征值的平方）
lambda = diag(S).^2;

% 计算卡方统计量
chi2Square = totalSum * (lambda);

% 计算总的卡方统计量
totalChi2Square = sum(chi2Square);

% 计算贡献率
contributionRate = lambda / sum(lambda);

% 计算累计贡献率
cumulativeRate = cumsum(contributionRate);

% 计算行轮廓坐标
beta = diag(rowRatio.^(-1 / 2)) * U_adjusted;
G = beta * S

% 计算列轮廓坐标
alpha = diag(columnRatio.^(-1 / 2)) * V_adjusted;
F = alpha * S

% 计算样本点的个数
numOfSample = size(G, 1);

% 计算坐标的取值范围
range = minmax(G(:, [1, 2])');

% 画图略

4.结果

详见上文分析过程，地区和指标点可以分为两类，

第一类包括指标点 $x_4,x_5$ ，地区点为北京、天津、河北、上海、江苏、浙江、山东；

第二类包括指标点 $x_1,x_2,x_3,x_6$ ，地区点为其余地区。

习题10.6（2）

1. 题目要求

同上。

2.解题过程——R型因子分析

解：

对数据进行标准化处理。

计算变量间的相关系数得出相关矩阵 $\mathbf{R}$ ，然后计算初等载荷矩阵 ${\mathbf{\Lambda }}_1$ 。

计算得到特征根与各因子的贡献如下表所示。

value	x1	x2	x3	x4	x5	x6
特征值	3.55842	1.316252	0.608239	0.373383	0.107178	0.036527
贡献率	59.30701	21.93754	10.13732	6.223052	1.786295	0.608786
累积贡献率	59.30701	81.24454	91.38187	97.60492	99.39121	100

选择 $m(m\le 6)$ 个主因子，构造因子模型：
$$\begin{array}{r}?\begin{array}{l}{\tilde{x}}_1={\alpha }_{11}{\tilde{F}}_1+{\alpha }_{12}{\tilde{F}}_2+{\alpha }_{13}{\tilde{F}}_3\\ ?\\ {\tilde{x}}_7={\alpha }_{71}{\tilde{F}}_1+{\alpha }_{72}{\tilde{F}}_2+{\alpha }_{73}{\tilde{F}}_3\end{array}\end{array}$$
求得因子载荷等估计。

最终，通过表格，可以看出，得到了3个因子，第一个因子是穿住用因子，第二个因子是燃料因子，第3个因子是文化因子。

第(1)问中得到 $x_4,x_5$ 是一类变量，这里得到 $x_2,x_4,x_5$ 是一类变量，略有差异。

3.程序

求解的MATLAB程序如下：

clc, clear 

% 原始数据，包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
    135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
    95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
    104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
    128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
    145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
    159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
    116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
    221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
    144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
    169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
    153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
    144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
    140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
    115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
    101.18, 23.26, 8.46, 20.20, 20.50, 4.30];

% 数据标准化
standardizedData = zscore(originalData);

% 计算相关性矩阵
correlationMatrix = corrcoef(standardizedData);

% 使用主成分分析方法对相关性矩阵进行处理，得到特征向量、特征值和贡献率
[eigenvectors, eigenvalues, contribution] = pcacov(correlationMatrix);

% 计算累积贡献率
cumulativeContribution = cumsum(contribution);

% 根据特征向量的符号进行调整
adjustedSigns = repmat(sign(sum(eigenvectors)), size(eigenvectors, 1), 1);
adjustedEigenvectors = eigenvectors .* adjustedSigns;

% 根据特征值进行缩放
scaledFactors = repmat(sqrt(eigenvalues)', size(adjustedEigenvectors, 1), 1);
scaledEigenvectors = adjustedEigenvectors .* scaledFactors;

% 计算贡献率
contribution1 = sum(scaledEigenvectors.^2);

% 选择的因子数量
factorNum = 3;

% 根据选择的因子数量得到对应的因子
selectedFactors = scaledEigenvectors(:, [1:factorNum]);

% 使用方差最大法进行因子旋转
[rotatedFactors, factorMatrix] = rotatefactors(selectedFactors, 'method', 'varimax')

% 合并旋转后的因子和其他因子
mergedFactors = [rotatedFactors, scaledEigenvectors(:, [factorNum + 1:end])];

% 计算因子载荷量
factorLoads = sum(rotatedFactors.^2, 2)

% 计算贡献率
contribution2 = sum(mergedFactors.^2)

% 计算每个因子的贡献率
contributionRate = contribution2(1:factorNum) / sum(contribution2);

% 计算因子得分系数矩阵
factorScoreCoefficients = inv(correlationMatrix) * rotatedFactors;

4.结果

求得因子载荷等估计如下表所示。

可以看出，得到了3个因子，第一个因子是穿住用因子，第二个因子是燃料因子，第3个因子是文化因子。

第(1)问中得到 $x_4,x_5$ 是一类变量，这里得到 $x_2,x_4,x_5$ 是一类变量，略有差异。

习题10.6（3）

1. 题目要求

同上。

2.解题过程——聚类分析

解：

首先计算变量间的相关系数。用两变量$x_j$与$x_k$的相关系数作为它们的相似性度量,即$x_j$与$x_k$的相似系数为
$$r_{jk}=\frac{{\sum }_{i=1}^{16}(a_{ij}?{\mu }_j)(a_{ik}?{\mu }_k)}{[{\sum }_{i=1}^{16}(a_{ij}?{\mu }_j{)}^2{\sum }_{i=1}^{16}(a_{ik}?{\mu }_k{)}^2{]}^{1/2}},j,k=1,\dots ,6.$$
然后计算6个变量两两之间的距离，构造距离矩阵。

接着使用最短距离法来测量类与类之间的距离,记类$G_p$和$G_q$之间的距离:
$$D(G_p,G_q)=\underset{i\in G_p,k\in G_q}{\min }{d}_{ik}.$$
变量聚类的结果是变量$x_3$自成一类，其他变量为一类。画出的变量聚类图如下图所示。

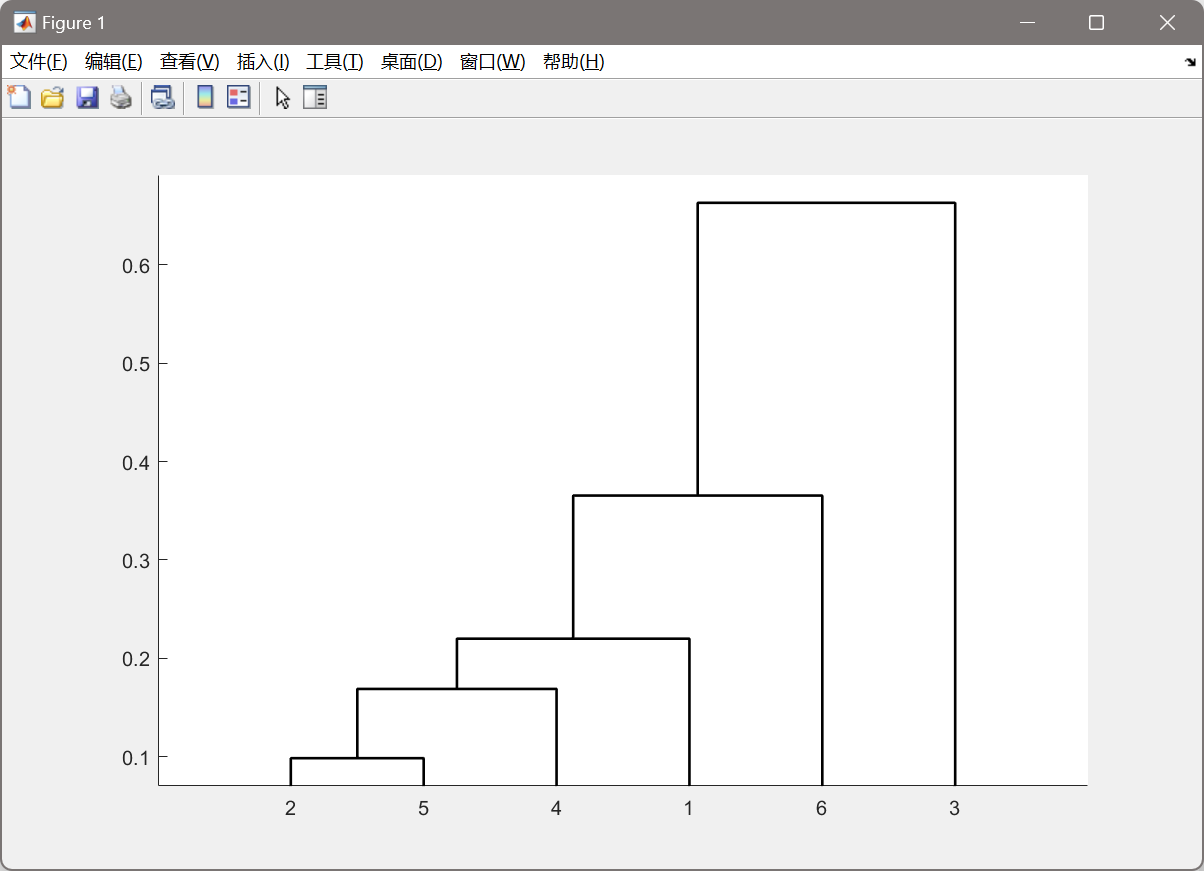
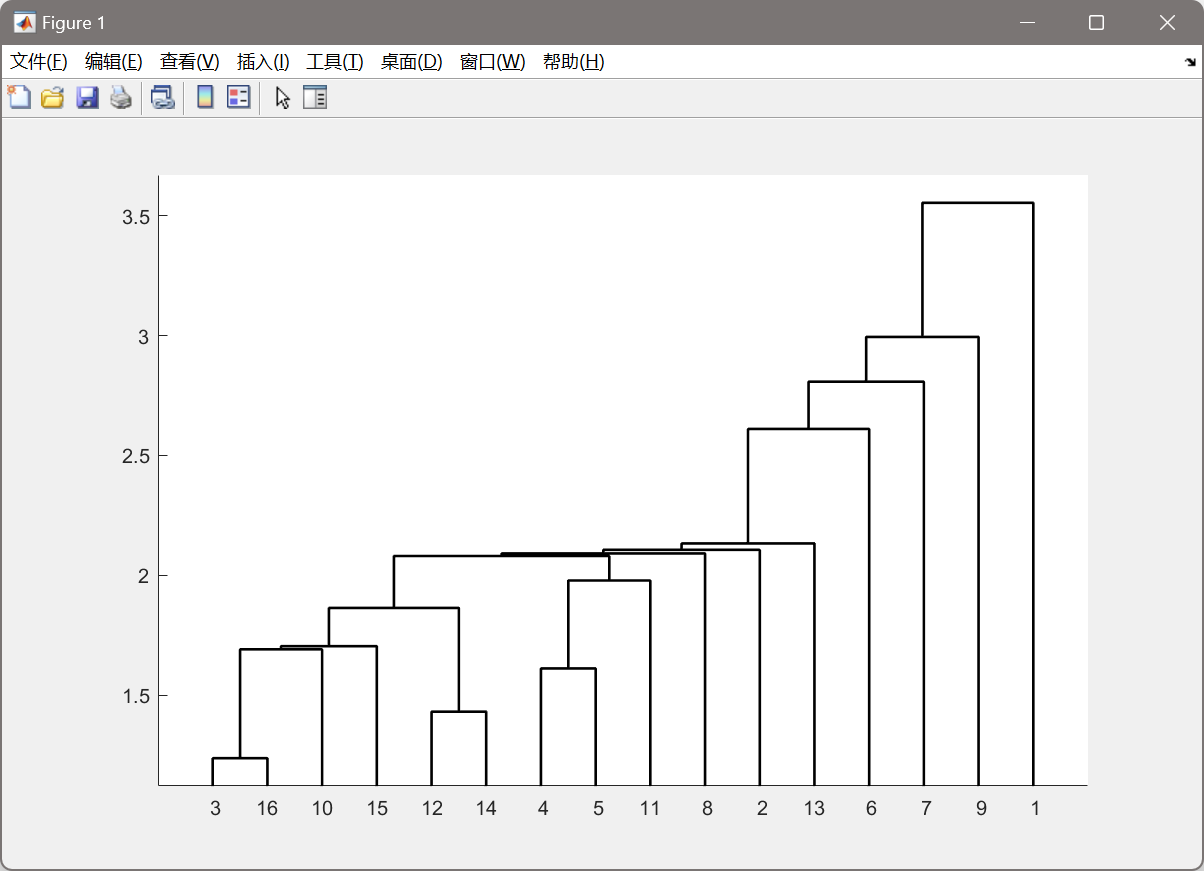
最后进行样本点聚类的$\mathbf{Q}$型聚类分析。

计算16个样本点之间的两两马氏距离。

类与类间相似性度量。

画聚类图，并对样本点进行分类。

样本点的聚类结果如下图所示。通过聚类图，可以把地区分成4类，北京自成一类，吉林自成一类，上海自成一类，其他地区为一类。

3.程序

求解的MATLAB程序如下：R型聚类

clc, clear 

% 原始数据，包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
    135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
    95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
    104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
    128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
    145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
    159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
    116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
    221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
    144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
    169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
    153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
    144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
    140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
    115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
    101.18, 23.26, 8.46, 20.20, 20.50, 4.30];

% 计算相关性矩阵
correlationMatrix = corrcoef(originalData);

% 计算距离矩阵
distanceMatrix = 1 - abs(correlationMatrix);
distanceMatrix = tril(distanceMatrix);

% 将距离矩阵转为一维向量
distanceVector = nonzeros(distanceMatrix);
distanceVector = distanceVector';

% 使用层次聚类算法进行聚类
linkageCluster = linkage(distanceVector);

% 选择最大聚类数量为2，得到每个样本的类别
clusterLabels = cluster(linkageCluster, 'maxclust', 2);

% 找到属于第一类的样本
index1 = find(clusterLabels == 1); 
index1 = index1'

% 找到属于第二类的样本
index2 = find(clusterLabels == 2); 
index2 = index2'

% 生成树状图
h = dendrogram(linkageCluster);

% 设置树状图的颜色和线条宽度
set(h, 'Color', 'k', 'LineWidth', 1.3)

求解的MATLAB程序如下：Q型聚类

clc, clear 

% 原始数据，包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
    135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
    95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
    104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
    128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
    145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
    159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
    116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
    221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
    144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
    169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
    153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
    144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
    140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
    115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
    101.18, 23.26, 8.46, 20.20, 20.50, 4.30];

% 计算原始数据的协方差
covarianceMatrix = cov(originalData);

% 初始化距离矩阵
distanceMatrix = zeros(size(originalData, 1));

% 计算Q型距离
for j = 1:15
    for i = j+1:16
        distanceMatrix(i,j) = sqrt((originalData(i,:) - originalData(j,:)) * inv(covarianceMatrix) * (originalData(i,:) - originalData(j,:))');
    end
end

% 将距离矩阵转为一维向量
distanceVector = nonzeros(distanceMatrix);
distanceVector = distanceVector';

% 使用层次聚类算法进行聚类
linkageCluster = linkage(distanceVector);

% 生成树状图
dendro = dendrogram(linkageCluster);

% 设置树状图的颜色和线条宽度
set(dendro,'Color','k','LineWidth',1.3)

4.结果

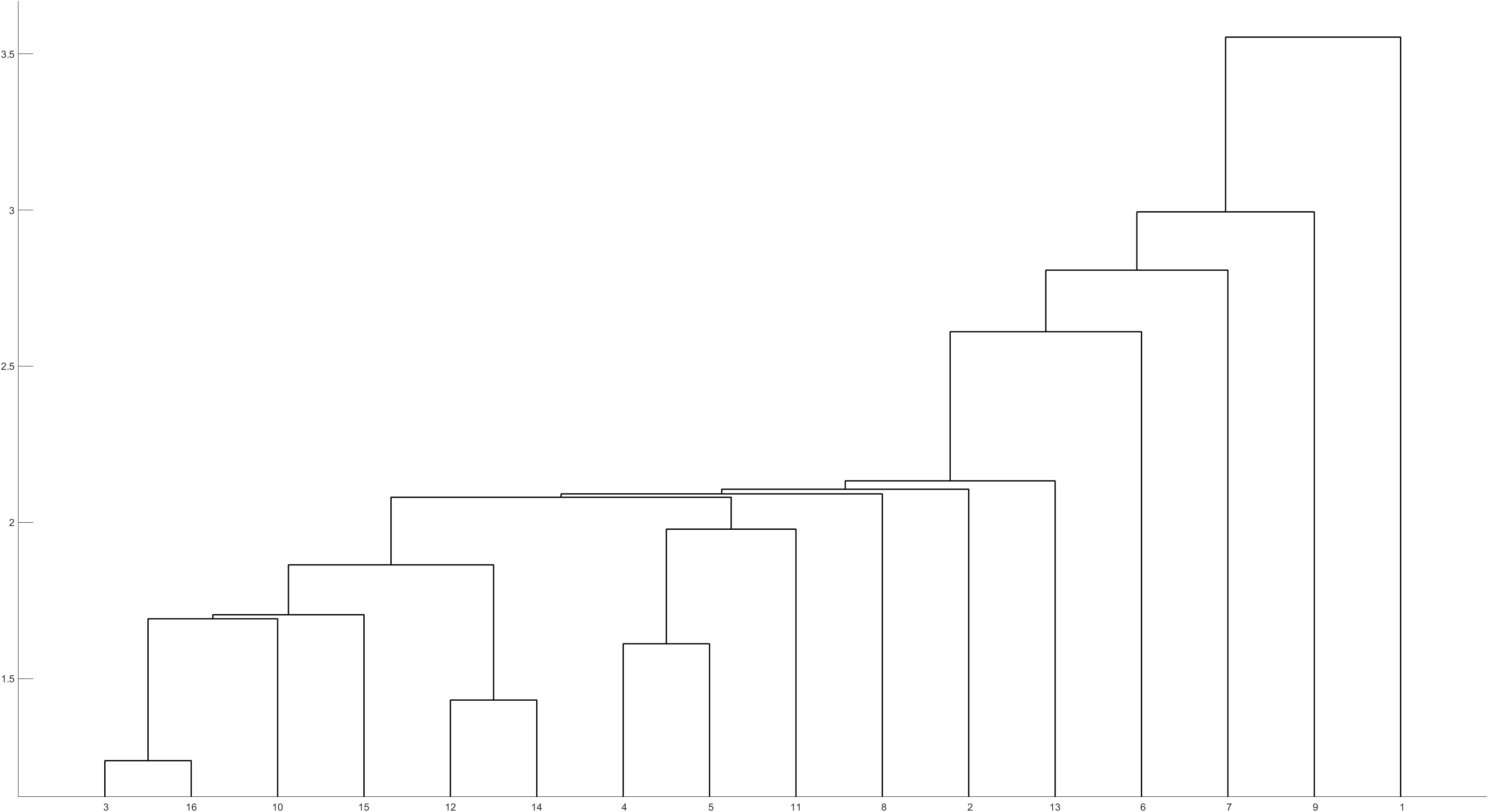
变量$x_3$自成一类，其他变量为一类。

北京自成一类，吉林自成一类，上海自成一类，其他地区为一类。

如果这篇文章对你有帮助，欢迎点赞与收藏~