2023年浙大城市学院新生程序设计竞赛(同步赛)G
发布时间:2023年12月24日
题意

 ?
?
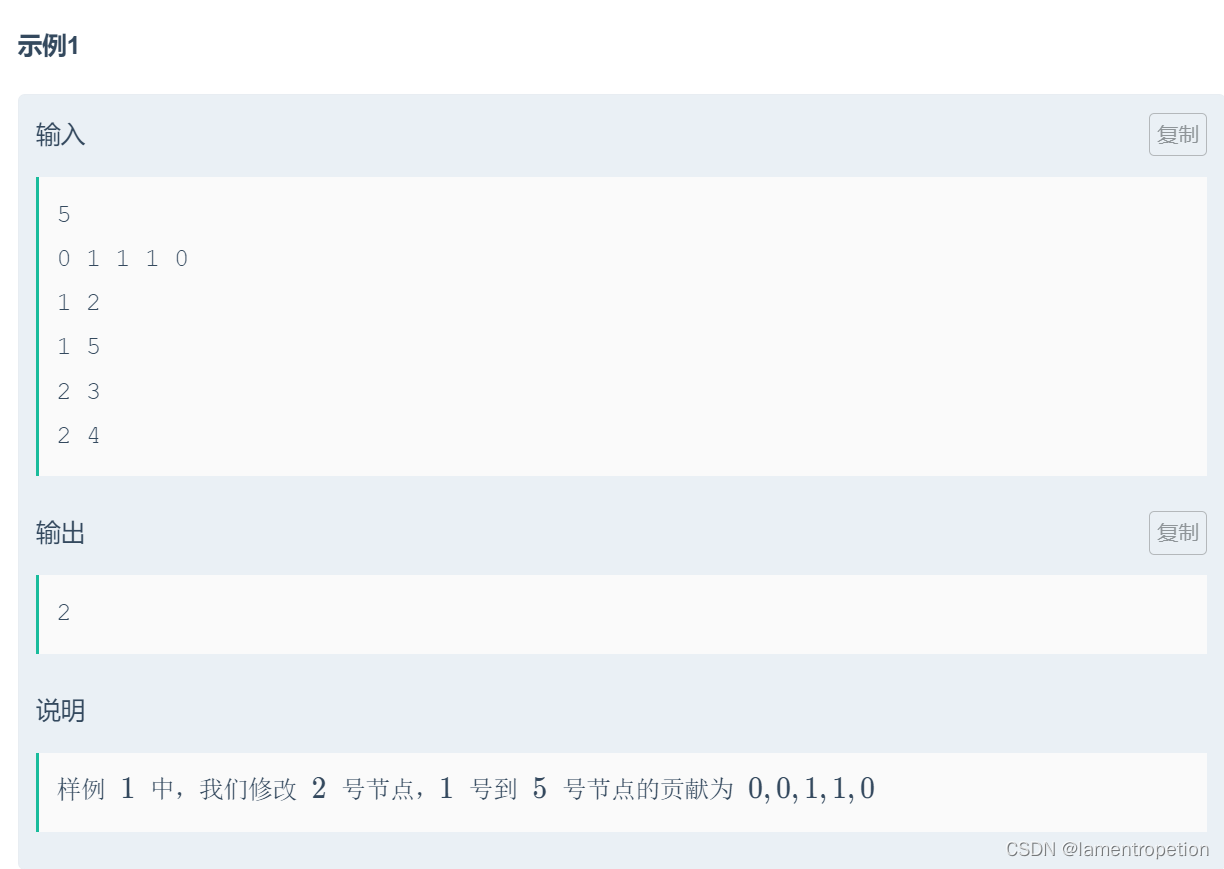 ?
?
思路
首先想法非常单一,一定是去枚举操作点,然后看它染白和不染的价值差值
也就是说,把一个黑色结点染白之后,对哪些结点的价值会影响
不难想象其实就是操作结点的子树和该点连通的黑色连通块的所有结点,对这些结点会有影响
那么差值其实就是黑色连通块大小 * 操作点到最近的白色祖先的距离
黑色连通块容易用树形dp求,然后就是操作点到最近白色祖先距离怎么求
dfs即可,记录上次的白色结点是什么即可
#include <bits/stdc++.h>
#define int long long
constexpr int N = 2e5 + 10;
std::vector<int> adj[N];
int n;
int a[N];
int lst[N];
int sz[N], dep[N], F[N][33];
int dp[N];
void dfs(int u, int fa) {
sz[u] = 1;
dep[u] = dep[fa] + 1;
F[u][0] = fa;
for (int i = 1; i <= 30; i++) {
F[u][i] = F[F[u][i - 1]][i - 1];
}
for (auto v : adj[u]) {
if (v == fa) continue;
dfs(v, u);
sz[u] += sz[v];
}
}
void dfs2(int u, int fa) {
if (a[u] == 1) dp[u] = 1;
for (auto v : adj[u]) {
if (v == fa) continue;
dfs2(v, u);
if (a[v] == 1) {
dp[u] += dp[v];
}
}
}
void dfs3(int u, int fa, int last) {
lst[u] = last;
for (auto v : adj[u]) {
if (v == fa) continue;
int clst = 0;
if (a[v]) {
clst = last;
}else {
clst = v;
}
dfs3(v, u, clst);
}
}
int lca(int u, int v) {
if (dep[u] < dep[v]) {
std::swap(u, v);
}
for (int j = 30; j >= 0; j --) {
if (dep[F[u][j]] >= dep[v]) {
u = F[u][j];
}
}
if (u == v) return u;
for (int j = 30; j >= 0; j --) {
if (F[u][j] != F[v][j]) {
u = F[u][j];
v = F[v][j];
}
}
return F[u][0];
}
int dis(int u, int v) {
return dep[u] + dep[v] - 2 * dep[lca(u, v)];
}
void solve() {
std::cin >> n;
for (int i = 1; i <= n; i ++) {
std::cin >> a[i];
}
for (int i = 1; i <= n - 1; i ++) {
int u, v;
std::cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1, 0);
dfs3(1, 0, 1);
for (int i = 1; i <= n; i ++) {
lst[i] = dis(i, lst[i]);
}
dfs2(1, 0);
int cur = 0;
for (int u = 1; u <= n; u ++) {
if (a[u] == 1) {
cur += lst[u];
}
}
int ans = cur;
for (int u = 1; u <= n; u ++) {
if (!a[u]) continue;
int res = cur;
res -= dp[u] * lst[u];
ans = std::min(ans, res);
}
std::cout << ans << "\n";
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
while(t --) {
solve();
}
return 0;
} ?
文章来源:https://blog.csdn.net/weixin_62528401/article/details/135176677
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 使用 Go 语言统计 0-200000 的数字中,哪些是素数?
- 【开题报告】基于SSM的企业排班系统的设计与实现
- Mysql数据库学习笔记
- 函数f的输入参数是多个单个值将函数f转化为:输入参数可以是数组的函数fv返回值数据类型是numpy数组fv=np.vectorize(f)
- zynq spi-emio的使用方法
- 中霖教育:专业不对口,能考会计师吗?
- 腾讯云短信验证配置
- Java Stream 中 filter 方法源码解析
- 【shell脚本实战案例】awk将科学计数法数字转为实数数字
- Linux文件操作命令(touch、cat、more、cp、mv、rm)