详解矩阵变换:伸缩,旋转,反射和投影
目录
一. 矩阵子空间
矩阵与向量相乘Ax可以看成子空间的变换。
零空间:输入向量x,输出Ax会变成零向量;
列空间:将Ax看成对矩阵列的组合;
矩阵A行的维度与输入向量x的维度一定是一样的,所以Ax也可以看成从行空间到列空间的转变。
二. 矩阵变换
假定矩阵为n行n列,且形成n维空间。输入的向量x也是n维的,Ax也就相当于得到了一个新的向量。很明显输入的空间为n维。接下来我们来看在相同空间内的四种矩阵变换:
2.1 伸缩矩阵
假定某矩阵为单位阵的倍数A=cI,如下:

那么Ax相当于对输入的向量扩张c倍,整个空间会延伸或压缩。当c为负数时,则沿着相反的方向操作,如下:

2.2 旋转矩阵
假定某矩阵如下:
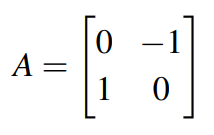
当输入为(x,y)时,输出可计算为:
很明显就是把输入(x,y)逆时针旋转90度,如下:
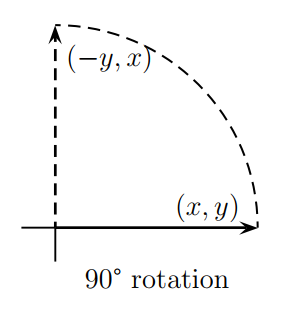
2.3 反射矩阵
发射矩阵也被称之为reflection matrix,标准形式如下:

当输入向量为(x,y)时,很明显输出为(y,x)。这两个点是关于y=x直线对称的。举个例子,如果输入点为(2,2),那么输出点也是(2,2),很有意思并没有改变。如果输入点为(2,-2),经过矩阵变换则变为(-2,2)。
如果将输入的两个点进行组合形成v,如下:
矩阵对第一个点相当于没有变换,对第二点转换x和y的位置,可得:
刚好对应上了。
实际上,投影矩阵也可以看成置换矩阵(permutation matrix),其直观的图像如下:

2.4 投影矩阵
投影矩阵也叫做projection matrix,其本质是将整个空间进行降低到子空间,该过程是不可逆的。标准的二维投影矩阵如下:
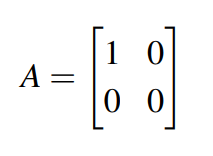
输入点为(x,y),经过矩阵变换后为(x,0),该点也是在x轴上且距离输入点最近的点。可以把此时的x轴看成矩阵A的列空间。原y轴上所有的点,都会被投影到(0,0),也就是其零空间(null space)。直观图像如下:
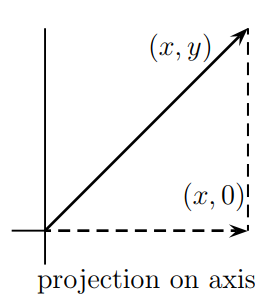
2.5 小结
以上例子可被之间推广到三维的情况。此处有一个非常有意思的总结:
There are matrices to stretch the earth or spin it or reflect it across the plane of the equator (forth pole transforming to south pole). There is a matrix that projects everything onto that plane (both poles to the center).
三. 矩阵变换与函数
根据以上讨论,我们可以把矩阵变换看成一种线性的函数转化,如下:
T(x)=Ax
3.1 原点
因为A0=0,所以任何矩阵对原点都是无可变换的。
3.2 常数倍性质
如果某矩阵可以把x变成x',那么当输入是2x时,输出肯定是2x'。当输入是cx时,输出肯定是cx',总结性质如下:
A(cx)=c(Ax)
当c=0时,此时也可以证明3.1中原点的性质。
3.3 加法性质
如果输入分别为x和y,对应的输出为x'和y',那么当输入为求和x+y时,输出也肯定为x'+y'。总结性质如下:
A(x+y)=Ax+Ay
矩阵的乘法满足如上的变换性质,满足以上也可以称之为线性变换(linear transformation)。
3.4 小结
对于任意的数c和d,任意的向量x和y,矩阵乘法满足如下线性法则:
A(cx+dy)=c(Ax)+d(Ay)
矩阵跟线性代数(linear algebra)的关系就是这么来的。
四. 空间变换
矩阵变换可以从到
。如果给出的矩阵A是m行n列的,那么就可以从n维向量变换到m维向量,换句话说长方形的矩阵(非方阵)也满足如上线性变换。
以上变换中的cx+dy中的x和y可以使多项式,可以是矩阵,还可以是函数x(t)和y(t),只要满足如上关系都可以看成线性变换。
举个例子,一个次数为n的多项式如下:
该多项式有n+1个系数,所以可以看成n+1维的向量。在网络安全等领域,这种理解经常会出现。
五. 小结
图像的几何变换是指将一幅图像中的坐标位置映射到另一张图像中的新坐标位置,几何变换包括平移、旋转、缩放、翻转、仿射变换、透视变换等。平移、旋转、缩放似乎是最为简单的几何变换,可以通过仿射变换实现。
仿射变换是将一个二维坐标转换到另一个二维坐标的过程。仿射变换是一种线性变换,变换前是直线的,变换后依然是直线;变换前是平行线的,变换后依然是平行线。仿射变换的概念如下图所示。变换前图像中的点 1、点 2、点 3(不在同一条直线上)与变换后图像中的点 1、点 2、点 3 一一对应。由于 3 点可以决定一个平面,所以利用这 3个点的对应关系就可以对整个图像平面进行仿射变换。仿射变换的范围很广,平移、旋转、缩放、翻转实际上都属于仿射变换。
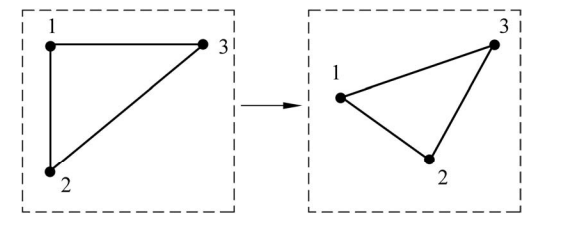
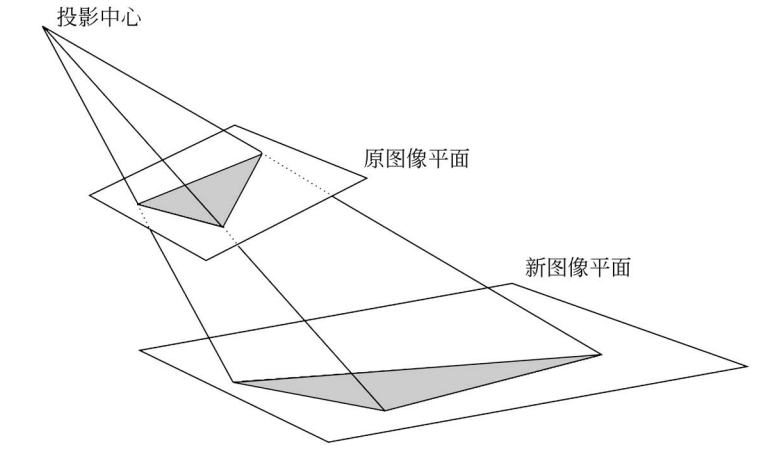
仿射变换又称三点变换,因为它只用到 3 个点,而透视变换则用到了 4 个点,因此也被称为四点变换。透视变换是利用投影成像的原理将物体重新投射到另一个成像平面,如下图。透视变换的转换矩阵也与仿射变换的矩阵不同,是一个 3×3 的矩阵。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!