第七章 图

在图结构中，结点间前驱和后继均可不唯一，即结点之间是多对多的关系

点集合中不能为空，边集合可以为空

图的存储结构：邻接矩阵、邻接表、十字链表及邻接多重表

图的遍历方法：广度优先搜索，深度优先搜索

稠密图：图中具有很多的边（普利姆算法）

稀疏图：图中具有很少的边（克鲁斯卡尔算法）

关键路径：拓扑排序

最短路径：迪杰斯特拉

最小生成树：prime算法，克鲁斯卡尔算法

深度优先搜索：按照深度方向搜索，类似于树的先根遍历（找邻点的邻点直到没有，再回溯）

广度优先搜索：按照广度方向搜索，类似于树的层次遍历（先找一个点的所有邻接点，同时访问，再继续同时访问下一个）

有向图：节点之间的边存在方向

无向图：节点之间的边不存在方向

一、dfs?

二、bfs

三、拓扑序列

?

1.?关于图的邻接矩阵，下列哪个结论是正确的？（B）

A.有向图的邻接矩阵总是不对称的

B.有向图的邻接矩阵可以是对称的，也可以是不对称的

C.无向图的邻接矩阵总是不对称的

D.无向图的邻接矩阵可以是不对称的，也可以是对称的

无向图的邻接矩阵一定是对称的；

有向图的邻接矩阵可以是对称的，也可以是不对称的

2.?下面给出的有向图中，各个顶点的入度和出度分别是：（A）

A.入度: 0, 2, 3, 1, 2; 出度: 3, 2, 1, 1, 1

B.入度: 3, 2, 1, 1, 1; 出度: 0, 2, 3, 1, 2

C.入度: 3, 4, 4, 2, 3; 出度: 3, 4, 4, 2, 3

D.入度: 0, 1, 2, 1, 1; 出度: 3, 2, 1, 1, 1

0 入度：0? ?出度：3

1 入度：2? ?出度：2

2 入度：3? ?出度：1

3 入度：1? ?出度：1

4 入度：2? ?出度：1

3.?设无向图为 G=(V，E)，其中 V={v1,v2,v3,v4}，E={(v1,v2)，(v3,v4)，(v4,v1)，(v2,v3)，(v1,v3)}。则相应的邻接矩阵为：（B）

A.

B.

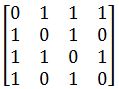
C.

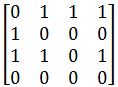
D.

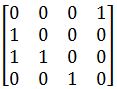
因为为无向图，所以 v1<->v2;v3<->v4;v4<->v1;v2<->v3;v1<->v3;?

?

4.?在图中自d点开始进行深度优先遍历算法可能得到的结果为：(C)

A.d,a,c,f,e,b

B.d,a,e,b,c,f

C.d,e,a,c,f,b

D.d,f,c,e,a,b

d->e,d->f.排除A,B选项

d->f->c（c之后只能选择a,不能没有走完就突然回溯到d）

5.?下列选项中，不是下图深度优先搜索序列的是：(D)

A.V1?,?V5?,?V4?,?V3?,?V2?

B.V1?,?V3?,?V2?,?V5?,?V4?

C.V1?,?V2?,?V5?,?V4?,?V3?

D.V1?,?V2?,?V3?,?V4?,?V5?

D选项中，V2走不到V3

6.?在图中自c点开始进行广度优先遍历算法可能得到的结果为：(C)

A.c,a,b,e,f,d

B.c,a,f,d,e,b

C.c,f,a,d,e,b

D.c,f,a,b,d,e

c a f b d e

c f a d b e

c f a d e b

7.?任何一个带权无向连通图的最小生成树(C)

A.是唯一的

B.是不唯一的

C.有可能不唯一

D.有可能不存在

8.已知有向图G=(V, E)，其中V = {v1, v2, v3, v4, v5, v6}，E = {<v1,v2>, <v1,v4>, <v2,v6>, <v3,v1>, <v3,v4>, <v4,v5>, <v5,v2>, <v5,v6>}。G的拓扑序列是：(A)

A.v3, v1, v4, v5, v2, v6

B.v3, v4, v1, v5, v2, v6

C.v1, v3, v4, v5, v2, v6

D.v1, v4, v3, v5, v2, v6

先找入度为0的点，边删边，边找入度为0的点

9.?我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题？（A）

A.Dijkstra算法（从顶点v0出发到其余顶点的最短路径算法）

B.Kruskal算法（最小生成素）

C.深度优先搜索（图的遍历）

D.拓扑排序算法（关键路径）

10.数据结构中Dijkstra算法用来解决哪个问题？(B)

A.关键路径

B.最短路径

C.拓扑排序

D.字符串匹配