图像处理 王伟强 作业

文章及资源来自优秀的师兄师姐们

hw_1

1. 对于给定的一幅输入灰度图像，我们首先通过图像的读取函数imread将该图像加载到内存中。假定存储该图像的矩阵元素为uint8数据类型，请设计利用幂律变换处理该图像的算法，并利用matlab代码实现该函数以及给出测试matlab代码。

   幂律变换的一般形式为：s=T( r )=c*r^γ
   其中，r为原始图像灰度值，γ为幂指数，c为尺度比较常数，s为幂律变换后的目标灰度值。

   首先将uint8类型的数据转换成浮点型double
   再套入公式s=T?=c*r^γ进行计算
   最后再将数据类型转回uint8输出

input = imread('D:\Desktop\v2-da5b3f5c9e21c51f4218fe8c9378a633_1440w.png'); 
gamma = 0.5;
output = power_law_transform(input, gamma);

subplot(1, 2, 1);
imshow(input);
title('原图');

subplot(1, 2, 2);
imshow(output);
title('变换后');

function output = power_law_transform(input, gamma)
    output = uint8(255 * (double(input) / 255).^gamma);
end

2. 利用分段函数进行亮度变换是一种具有很好通用性有效图像增强方法。我们通常要选择一些控制点，相邻控制点可以确定对应区间内的一条映射直线。请问：当该直线的斜率k=1,\ k>1,\ 0<k<1三种情况下，能起到怎样的图像处理作用？另外，请进一步思考讨论k<0的情况。

   当k=1时：图像保持原始的亮度，不会改变图像的对比度
   当k>1时：图像的亮度将增加，图像将会变得更亮，增强图像的对比度，图 像看起来更加清晰
   当0<k<1时：图像的亮度将减小，图像将会变得更暗，减小了图像的对比度， 图像看起来变暗
   当k<0时：图像原来较亮的区域将变暗，原来较暗的区域将变亮，图像的亮度反转

3. 一幅8灰度级图像具有如下所示的直方图，求直方图均衡后的灰度级和对应概率，并画出均衡后的直方图的示意图。（图中的8个不同灰度级对应的归一化直方图为[0.17 0.25 0.21 0.16 0.07 0.08 0.04 0.02]）
   
   
   

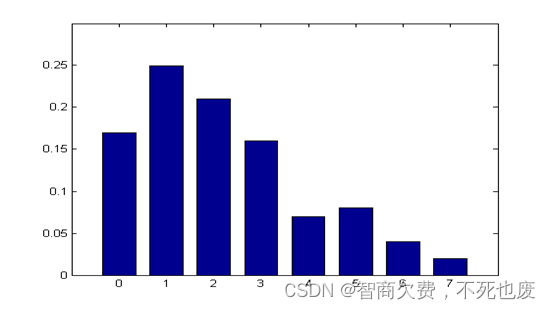
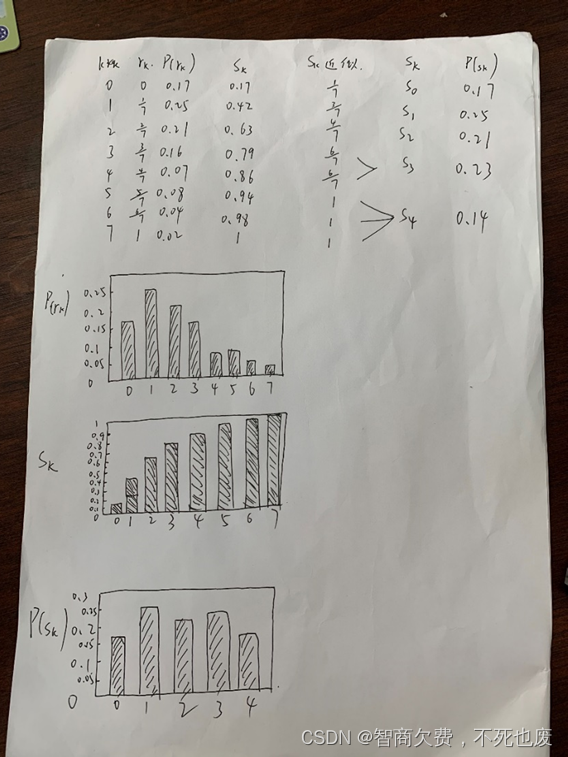
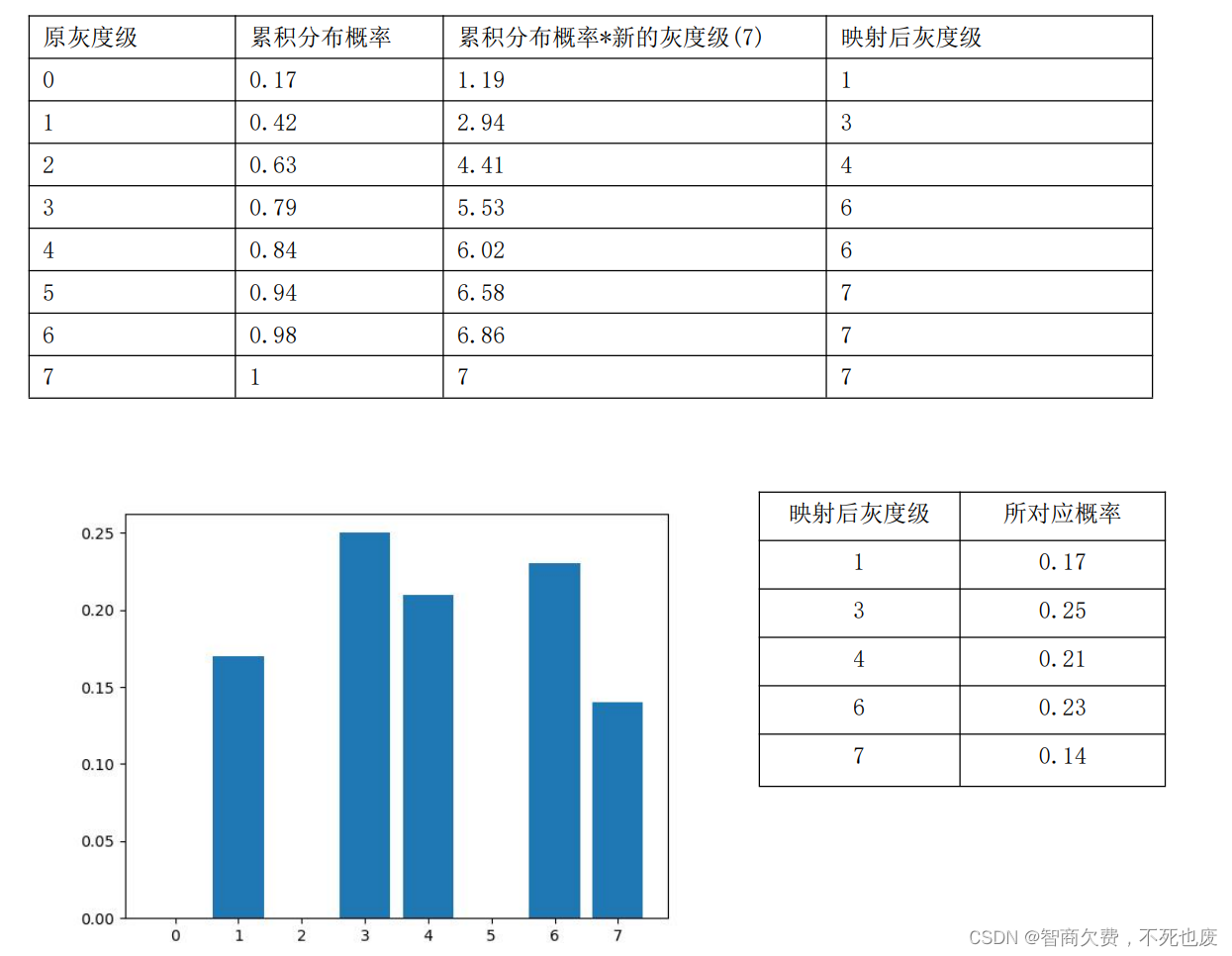
hw_2

1. 完成课本数字图像处理第二版114页，习题3.10。
   $P_r(r)={\int }_0^r(2?2w)dw=2r?r^2$

   $P_z(z)={\int }_0^{z}2wdw=z^2$

   $z=\sqrt{2r?r^2}$

2. 卷积是用来描述线性移不变系统的。
   （1）请用数学语言定义描述定义什么是线性移不变系统？
   （2）请证明卷积具有交换性；
   （3）请证明卷积是一种线性运算；
   （4）请证明任何函数f\left(x\right)与单位脉冲函数进行卷积时，结果为该函数本身。
   （5）(选作) 说明卷积是线性移不变系统的数学描述
   （注意： 证明采用连续或者离散形式都可以）
   

3. 课本数字图像处理第二版116页，习题3.25，即拉普拉斯算子具有理论上的旋转不变性。
   

4. 请计算如下两个向量与矩阵的卷积计算结果。
   （1） [ 1 2 3 4 5 4 3 2 1] *[ 2 0 -2]
   （2）
   $\left[\begin{array}{ccc}?1& 0& 1\\ ?2& 0& 2\\ ?1& 0& 1\end{array}\right]?\left[\begin{array}{ccccc}1& 3& 2& 0& 4\\ 1& 0& 3& 2& 3\\ 0& 4& 1& 0& 5\\ 2& 3& 2& 1& 4\\ 3& 1& 0& 4& 2\end{array}\right]$

[ 1 2 3 4 5 4 3 2 1]*[ 2 0 -2] = -4
[ 1 2 3 4 5 4 3 2 1] *[ 2 0 -2] = -4
[ 1 2 3 4 5 4 3 2 1] *[ 2 0 -2] = -4
[ 1 2 3 4 5 4 3 2 1] *[ 2 0 -2] = 0
[ 1 2 3 4 5 4 3 2 1] *[ 2 0 -2] = 4
[ 1 2 3 4 5 4 3 2 1] *[ 2 0 -2] = 4
[ 1 2 3 4 5 4 3 2 1] *[ 2 0 -2] = 4

故[ 1 2 3 4 5 4 3 2 1] *[ 2 0 -2] = [ -4 -4 -4 0 4 4 4]

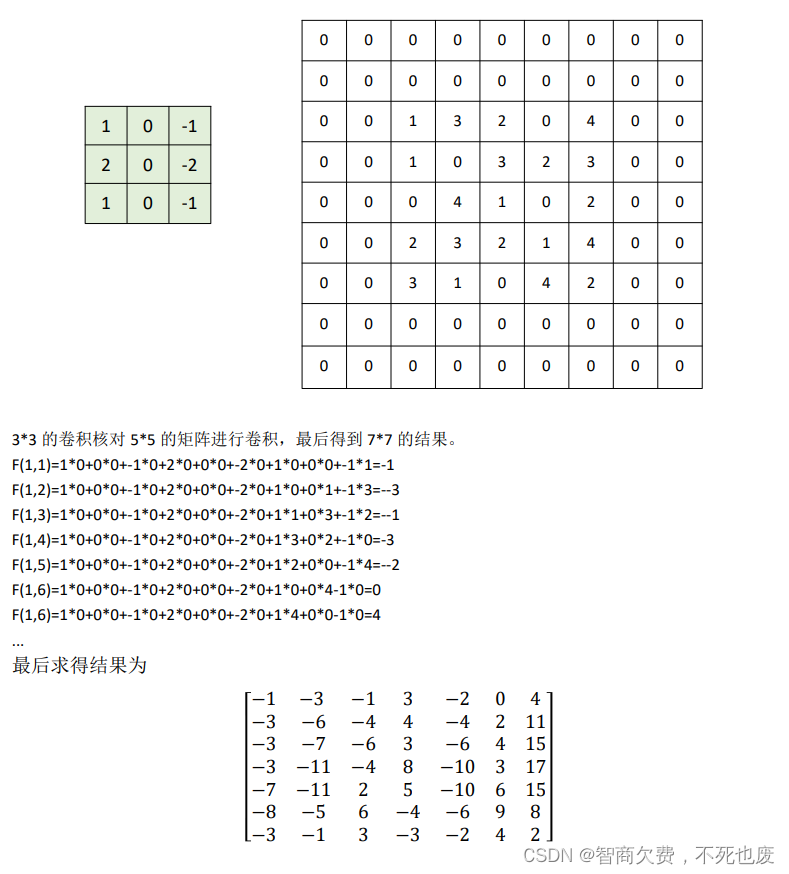
hw_3

1. 根据书中对傅立叶变换的定义，证明课本165页上有关傅立叶变换的平移性质。
   $F(u,v)=\frac{1}{MN}{\sum }_{x=0}^{M?1}{\sum }_{y=0}^{N?1}f(x,y)e^{?j2\pi (\frac{ux}{M}+\frac{vy}{N})}$

$F\left(u?u_0,v?v_0\right)$

$=\frac{1}{MN}{\sum }_{x=0}^{M?1}{\sum }_{y=0}^{N?1}f\left(x,y\right)e^{?j2\pi \left(\frac{x\left(u?u_0\right)}{M}+\frac{y\left(v?v_0\right)}{N}\right)}$

$=\frac{1}{MN}{\sum }_{x=0}^{M?1}{\sum }_{y=0}^{N?1}f\left(x,y\right)e^{?j2\pi \left(\frac{ux}{M}+\frac{vy}{N}\right)}{e}^{j2\pi \left(\frac{u_{0}x}{M}+\frac{v_{0}y}{N}\right)}$

$=f\left(x,y\right)e^{j2\pi (\frac{u_{0}x}{M}+\frac{v_{0}y}{N})}$

（2）
$f(x,y)={\sum }_{x=0}^{M?1}{\sum }_{y=0}^{N?1}F(u,v)e^{j2\pi (\frac{ux}{M}+\frac{vy}{N})}$

$f\left(x?x_0,y?y_0\right)$

$={\sum }_{x=0}^{M?1}{\sum }_{y=0}^{N?1}F\left(u,v\right)e^{j2\pi \left(\frac{u\left(x?x_0\right)}{M}+\frac{v\left(y?y_0\right)}{N}\right)}$

$={\sum }_{x=0}^{M?1}{\sum }_{y=0}^{N?1}F\left(u,v\right)e^{j2\pi \left(\frac{ux}{M}+\frac{vy}{N}\right)}{e}^{?j2\pi \left(\frac{u_{0}x}{M}+\frac{v_{0}y}{N}\right)}$

$=F(u,v)e^{?j2\pi (\frac{u_{0}x}{M}+\frac{v_{0}y}{N})}$

2. 观察如下所示图像。右边的图像这样得到：(a)在原始图像左边乘以\left(-1\right)^{x+y}；(b) 计算离散傅里叶变换(DFT); ? 对变换取复共轭; (d) 计算傅里叶反变换; (d) 结果的实部再乘以\left(-1\right)^{x+y}。(用数学方法解释为什么会产生右图的效果。)

4. 第二版课本习题4.21
左右两种填充方式可以得到相同的结果，但关键在于确保有足够的填充以获得适当的间距，将非周期函数，看做周期函数，方便傅里叶展开。

4. 第二版课本习题 4.21
进行图像延拓的目的在于避免在卷积处理后因为处理后图像变宽而影像边缘像素相互
影响而出现的混叠现象，填充 0 是为了增加一个缓冲区域，无论是对行列末尾填充 0
还是保持图像在中心周围填充 0，将填充后图像进行周期性延拓后都出现中心为图片，
周围补零现象，而且两种方法填充 0 的个数相同所以两种延拓方式没有区别

hw_5

hw_6

hw_7

hw_8

hw_9

1. 现在假设我们有一个长度为8的信号f=[1 3 5 7 4 3 2 1], 利用哈尔小波进行两层的快速小波变换分解，计算各层的滤波器输出，然后再进行完美重建，请利用与书中例子相同的框图进行计算。
   
   

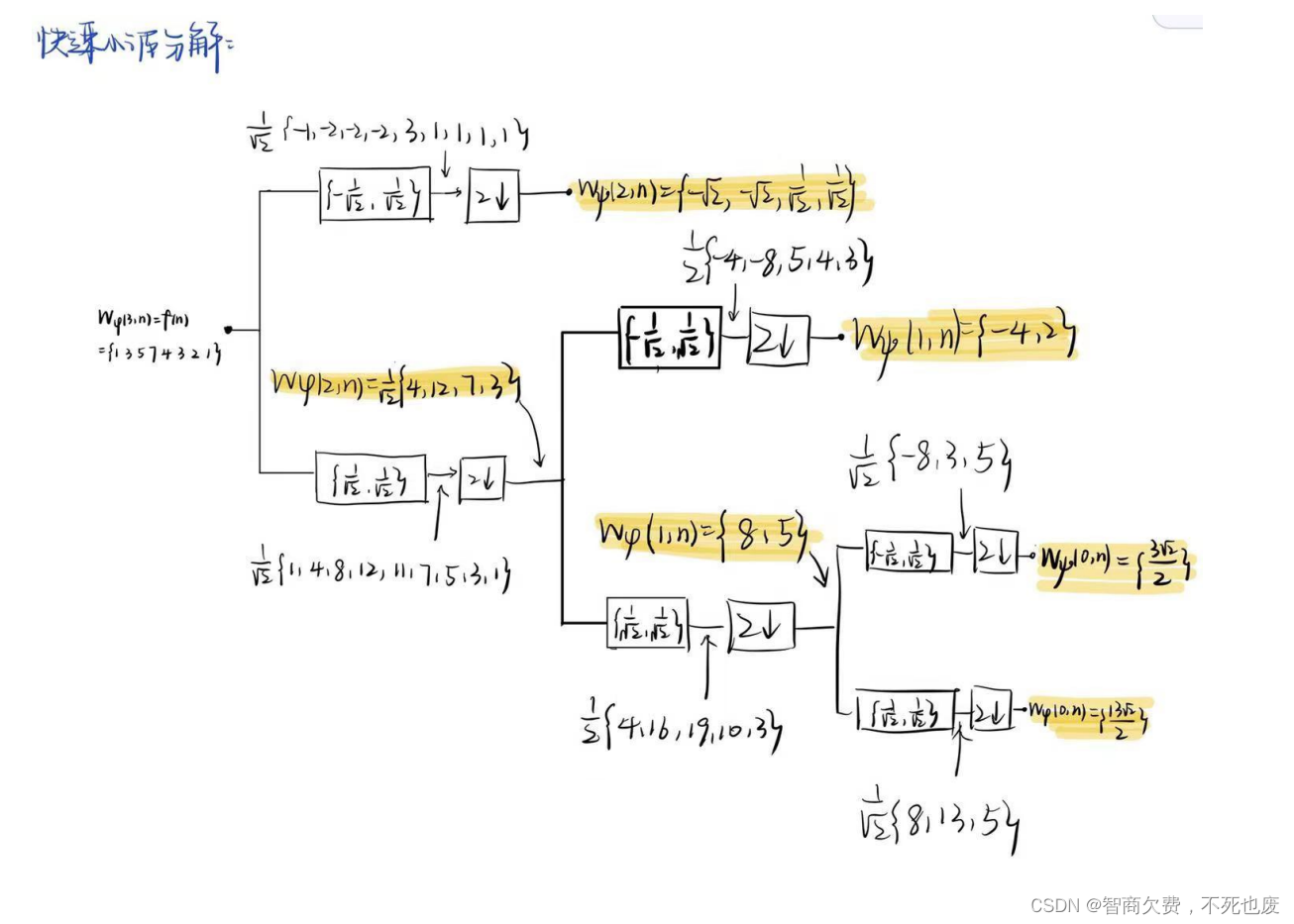
2. 小波包是一种可以根据需要对信号进行更多控制的时间/空间-频率分解的工具。它的一种应用是对图像信息的压缩。课本中给出了一个针对指纹图像进行压缩的实例，在该实例中一幅指纹图像可以被至多分解成深度为4的小波包分解树。请计算进行至多4级小波包分解共有多少分解方式？请形式化描述一个基于书中能量函数定义的最优小波包分解树的构建算法（给出计算的流程，假设至多分解深度为N）

$$\begin{gathered} 一个P尺度的二维小波包树支持：D\left(P+1\right)={\left[D\left(P\right)\right]}^4+1个唯一展开， \\ D（1）=1，故指纹图像的4级小波包共有 \\ D\left(4+1\right)={\left[D\left(4\right)\right]}^4+1={83552}^4+1=48733477265254383617种唯一展开 \end{gathered}$$

$D(2)=[D(1){]}^4+1=2$
$D(3)=[D(2){]}^4+1=17$
$D(4)=[D(3){]}^4+1=83552$
$D(5)=[D(4){]}^4+1=48733477265254383617$

算法：

• Step1 初始化：开始时，树的根节点为原始信号的近似系数或细节系数。
• Step2 逐层分析：
  • 从根节点开始，逐层向下遍历树，直到达到深度N或遍历完所有节点。
  • 对于每个父节点：
    • 计算父节点的能量Ep。
    • 分别计算四个后代节点的能量 Ea, Eh, Ev, Ed，这些节点代表滤波后的近似、水平细节、垂直细节、对角线细节。
• Step3 能量比较：
  • If (Ea+Eh+Ev+Ed < Ep)：
    • 保留这四个后代节点
    • 对于每一个新的后代节点，重复Step2。
  • Else(Ea+Eh+Ev+Ed ≥ Ep)：
    • 删除这四个后代节点，并只保留父节点。
• Step4 继续逐层分析：
  • 对于每一个新的子节点（如果存在），重复Step2和Step3，直到达到深度N或所有节点都被遍历。

$

hw_?