高频电子线路——串联谐振、并联谐振总结

发布时间：2024年01月03日

前言

最近在学习高频电子线路中的串联谐振回路和并联谐振回路相关知识，特以此文进行总结、归纳，以便日后进行查询和复习。

串联谐振（电压谐振）并联谐振（电流谐振）
定义由信号源与电容、电感串联构成的振荡回路由信号源与电容、电感线圈并联的振荡回路
电路图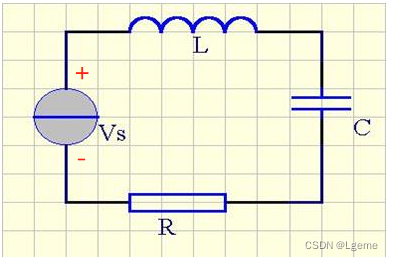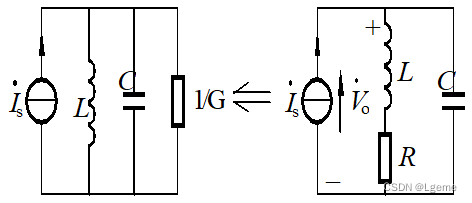
阻抗Z=R+j(\omega L-\frac{1}{\omega C})

?阻抗、

导纳、

谐振电阻R_{p}?

Z=\frac{(R+j\omega L)\frac{1}{j\omega C}}{R+j\omega L+\frac{1}{j\omega C}}\approx \frac{\frac{L}{C}}{R+j(\omega L-\frac{1}{\omega C})}=\frac{1}{\frac{RC}{L}+j(\omega C-\frac{1}{\omega L})}

Y=\frac{RC}{L}+j(\omega C-\frac{1}{\omega L})

R_{p}=\frac{L}{RC}

回路电抗X=\omega L-\frac{1}{\omega C}回路电纳B=\omega C-\frac{1}{\omega L}
回路电流\dot{I}=\frac{V_{s}}{Z}=\frac{V_{s}}{R+j(\omega L-\frac{1}{\omega C})}并联回路两端电压\dot{V}=\dot{I_{s}}Z=\frac{\dot{I_{s}}}{\frac{RC}{L}+j(\omega C-\frac{1}{\omega L})}
谐振频率

\omega _{0}L-\frac{1}{\omega _{0}C}=0

\omega _{0}=\frac{1}{\sqrt{LC}}

谐振频率

\omega _{p}L-\frac{1}{\omega _{p}C}=0

\omega _{p}=\frac{1}{\sqrt{LC}}

回路电流达到最大值\dot{I_{0}}=I_{max}=\frac{V_{s}}{R}并联两端电压达到最大值\dot{V_{p}}=V_{max}=I_{s}R_{p}
电抗与频率关系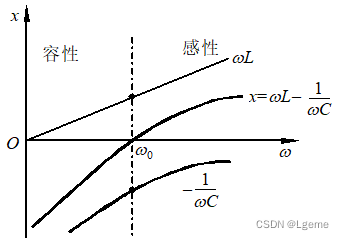电纳与频率关系

?特性阻抗\rho

\rho =\omega _{0}L=\frac{1}{\omega _{0}C}

?特性阻抗\rho

\rho =\omega _{p}L=\frac{1}{\omega _{p}C}
品质因数Q=\frac{\omega _{0}L}{R}=\frac{1}{\omega _{0}CR}=\frac{\rho }{R}品质因数

Q_{p}=\frac{\omega _{p}L}{R}=\frac{1}{\omega _{p}CR}=\frac{\rho }{R}

Q_{p}=\frac{R_{p}}{\omega _{p}L}=R_{p}\omega _{p}C

Q_{p}=\frac{\frac{1}{\omega _{p}L}}{G}=\frac{\omega _{p}C}{G}

电感、电容两端电压

\dot{V}_{L0}=\dot{I_{0}}j\omega _{0}L=\frac{\dot{V_{s}}}{R}j\omega _{0}L=j\frac{\omega _{0}L}{R}\dot{V_{s}}=jQ\dot{V_{s}}

\dot{V_{c0}}=\dot{I_{0}}\frac{1}{j\omega _{0}C}=-j\frac{1}{\omega _{0}CR}\dot{V_{s}}=-jQ\dot{V_{s}}

电容、电感的支路电流

\dot{I_{cp}}=\frac{\dot{V_{0}}}{\frac{1}{j\omega _{p}C}}=j\omega _{p}C\dot{I_{s}}R_{p}=jQ_{p}\dot{I_{s}}

I_{Lp}=\frac{\dot{V_{0}}}{j\omega _{p}L}=\frac{R_{p}\dot{I_{s}}}{j\omega _{p}L}=-jQ_{p}\dot{I_{s}}

谐振曲线表达式

\frac{I}{I_{0}}=\frac{1}{\sqrt{1+Q^{2}(\frac{\omega }{\omega _{0}}-\frac{\omega _{0}}{\omega })^{2}}}

? ? ??\approx \frac{1}{\sqrt{1+(Q\frac{2\Delta \omega }{\omega _{0}})^{2}}}

并联谐振曲线表达式

\frac{V}{V_{0}}=\frac{1}{\sqrt{1+Q^{2}(\frac{\omega }{\omega _{p}}-\frac{\omega _{p}}{\omega })^{2}}}

? ? ??\approx \frac{1}{\sqrt{1+(Q\frac{2\Delta \omega }{\omega _{p}})^{2}}}

广义失谐系数\xi =\frac{X}{R}=\frac{\omega L-\frac{1}{\omega C}}{R}=\frac{\omega_{0}L}{R}(\frac{\omega }{\omega _{0}}-\frac{\omega _{0}}{\omega })\approx Q\frac{2\Delta \omega }{\omega _{0}}广义失谐系数

\xi =\frac{B}{G}=\frac{\omega C-\frac{1}{\omega L}}{G}=\frac{\omega _{p}C}{G}(\frac{w}{w_{p}}-\frac{\omega _{p}}{\omega })

\approx 2\frac{\Delta \omega }{\omega _{p}}

串联振荡电路谐振曲线

Q值大曲线尖锐，选择性好，Q值小曲线钝，通带宽

并联振荡电路谐振曲线

Q值大曲线尖锐，选择性好，Q值小曲线钝，通带宽

通频带B=\frac{\omega _{0}}{Q}通频带B=\frac{\omega _{p}}{Q_{p}}
考虑电源内阻和负载

Q=\frac{\omega _{0}L}{R}=Q_{0}

Q_{L}=\frac{\omega _{0}L}{R+R_{L}+R_{S}}

Q_{L}<Q_{0}

结论：

1：Rs+RL使回路Q值降低，从而使谐振曲线变钝

2：串联谐振回路通常适用于信号源内阻Rs很小（恒压源）和负载电阻RL也不大的情况

考虑电源内阻和负载

结论：

并联谐振适合电源内阻和负载很大的电路

总结：

以上就是对串联谐振电路和并联谐振电路性质的总结，谢谢你能观看到这。

文章来源:https://blog.csdn.net/weixin_56646002/article/details/126813659
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章