将正规文法转化为正规式

将正规文法转化为正规式有以下几个规则：

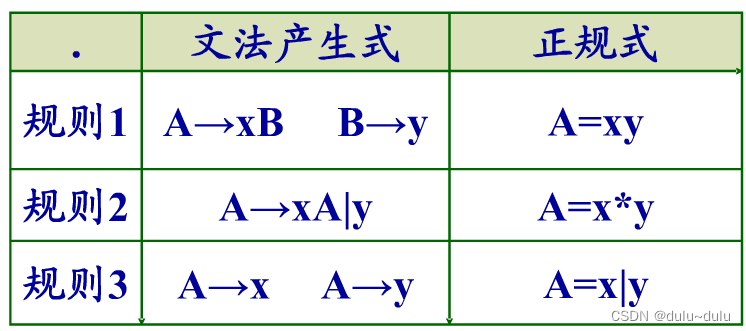
通过一道例题来讲解：

①A-->aC|bA

②C-->bD

③D-->aC|bD|

(1)首先将②带入③（不能将自身带入自身例如D-->aC|bD|,文法中带D，不能带入D）

D=abD|bD|=（ab|b）D |?，所以对应规则2(A-->xA|y),其中"(ab|b)"对应的是x，y对应的是

所以④D=x*y=(ab|b)*=(ab|b)*

(2)继续将②带入①:

⑤A=abD|bA

(3)将④带入⑤：

A=ab（ab|b）*|bA = bA|ab(ab|b)*，同样对应规则2，得到A=b*ab(ab|b)*

所以最后的结果为

A=b*ab(ab|b)*

C=bD

D=(ab|b)*

再来一道例题：?

?S→aA|a

?A→aA|dA|a|d

解如下：?

S = aA|a????????????????

A = (aA|dA)|(a|d)=(a|d)A|(a|d)

由规则二: A = (a|d)*(a|d)

代入得: S = a(a|d)*(a|d)|a = a(a|d)*(a|d)|ε= a(a|d)*

?注：这里(ald)(ald)和(ald)是等价的，因为它们都表示任意多个(a或d)的组合。