【论文阅读】Automated Runtime-Aware Scheduling for Multi-Tenant DNN Inference on GPU

该论文发布在 ICCAD’21 会议。该会议是EDA领域的顶级会议。

基本信息

Author	Hardware	Problem	Perspective	Algorithm/Strategy	Improvment/Achievement
Fuxun Yu	GPU	Resource under-utilization Contention	SW Scheduling	Operator-level scheduling ML-based scheduling auto-search	Reduced inference makespan

论文作者

Fuxun Yu 是一名来自微软的研究员。主要研究的是大规模深度学习服务系统。上一次看它的论文是一片关于该领域的综述，感觉写的蛮不错的。

背景

现在深度学习特别特别地火，multi-tenant DNN inference 也变成一个比较重要的问题。那什么是 multi-tenant DNN inference 呢？简而言之，就是研究如何让 GPU 同时运行不同模型推理。现有解决 multi-tenant DNN inference 问题的主要方法有两种：sequential exection 和 parallel/concurrent exection。

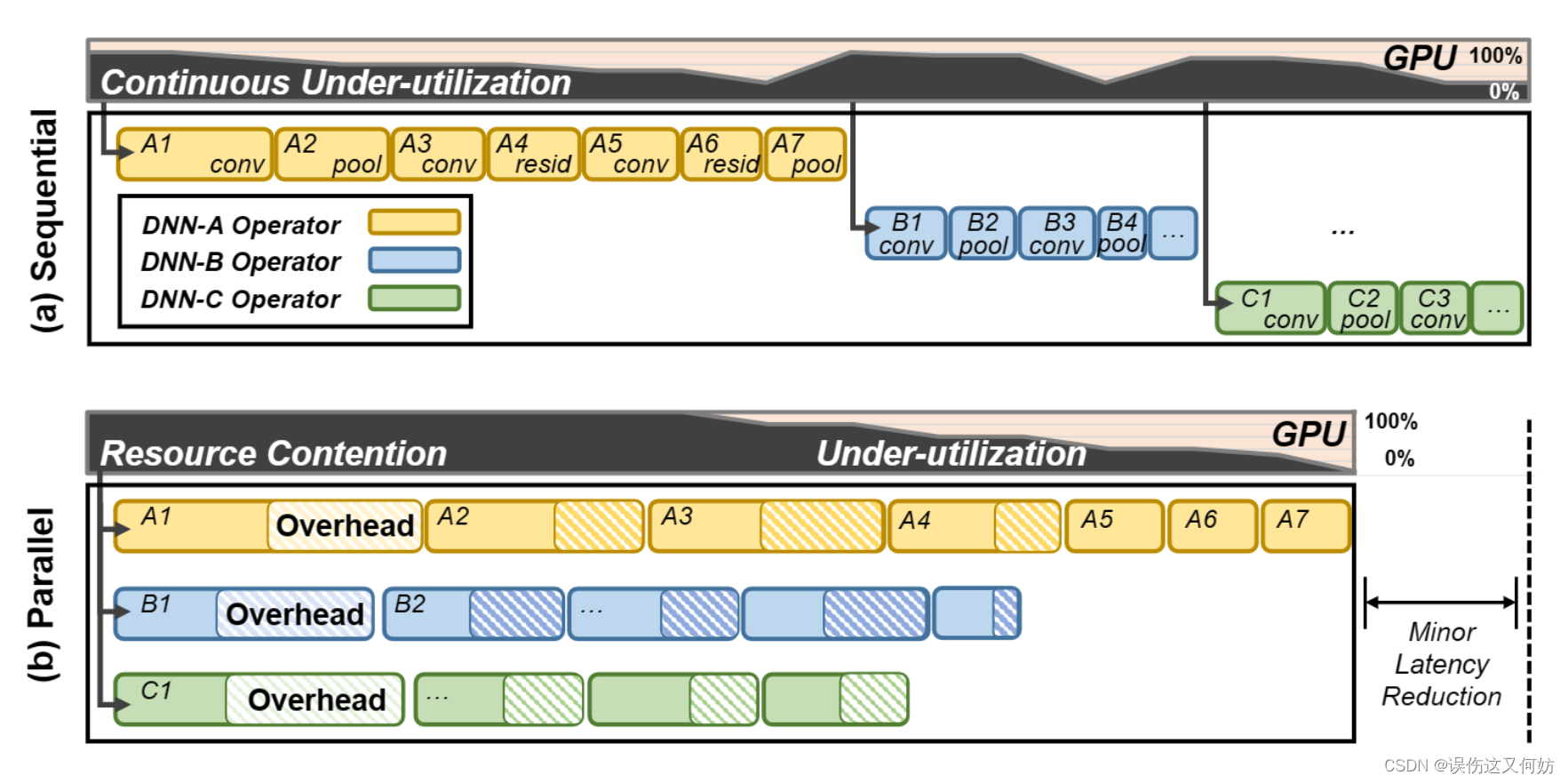
但这两种方式对于 GPU 资源利用不够充分。第一种方法（Sequential）由于是串行计算，自然GPU利用会比较低。第二种方法（Parallel）尽管前期提高了 GPU 的利用率，但当有的模型层数比较深，有的模型比较浅时，还会出现不平衡的现象。而且，由于GPU和内存资源争用，会产生高额的格外开销。
为此，希望提出一个新的解决方案，该解决方法能够进一步提高资源的利用率从而降低 latency。

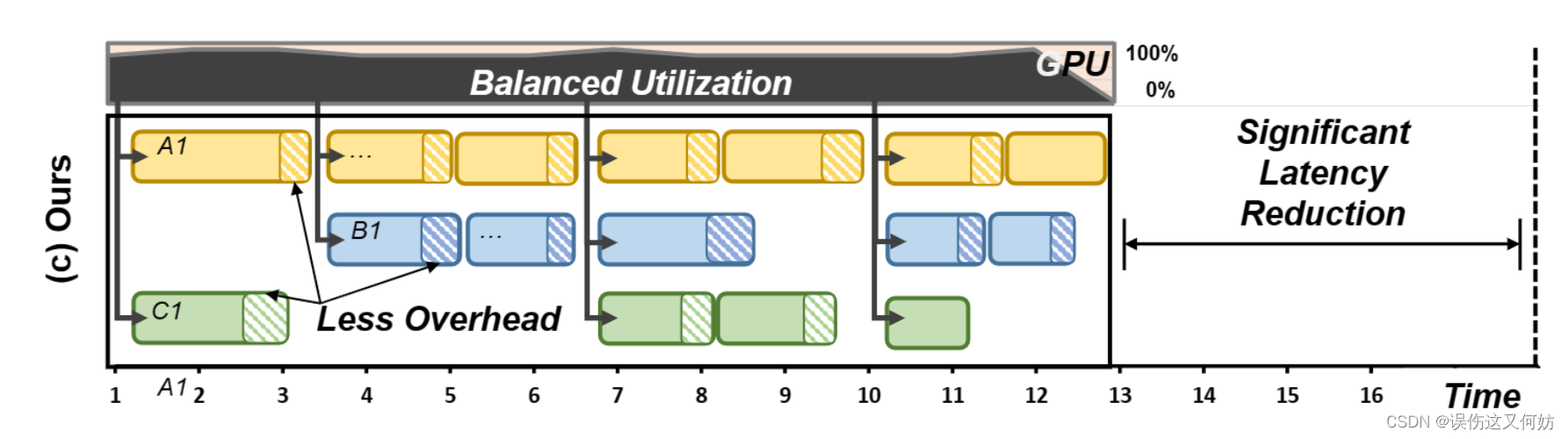
Schedualing Framework

multi-tenant schedule的关键点在于如何管理运行时的一致性以及平衡资源利用率。

基本思想

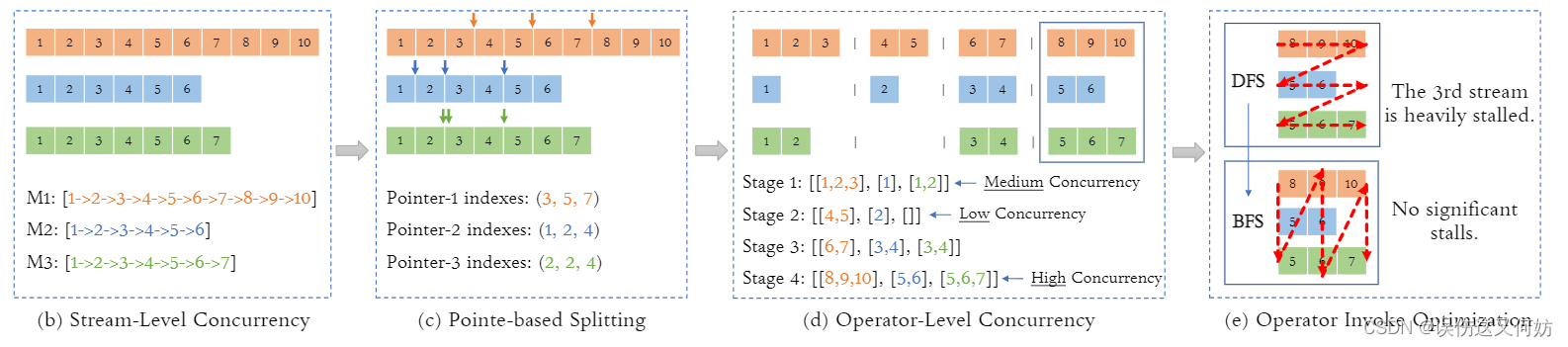
对于 Stream-Level 并行而言， 每个 GPU 流都会分配一个执行序列以实现不同模型并行推理。同时，如果要实现更细粒度的调度，这里引入一个概念 ---- 「pointers」。在插入同步阻碍（synchronization barries）的地方叫pointer。这样会将一个执行序列分成多个stage，这种拆分操作可以保证只有同一stage的操作才共享资源。我们可以通过调整pointers的位置而改变每个阶段的操作数量，从而找出最优的资源利用率策略。最后，状态内也做了一点优化，传统的DFS调动策略会导致GPU流之间存在优先级，导致停滞时间很长，因此改成使用BFS调度策略，使每个操作都得到执行。

这里有一个最关键的地方就是状态如何划分。接下来重点讲解这一部分。

Automated Scheduling Search

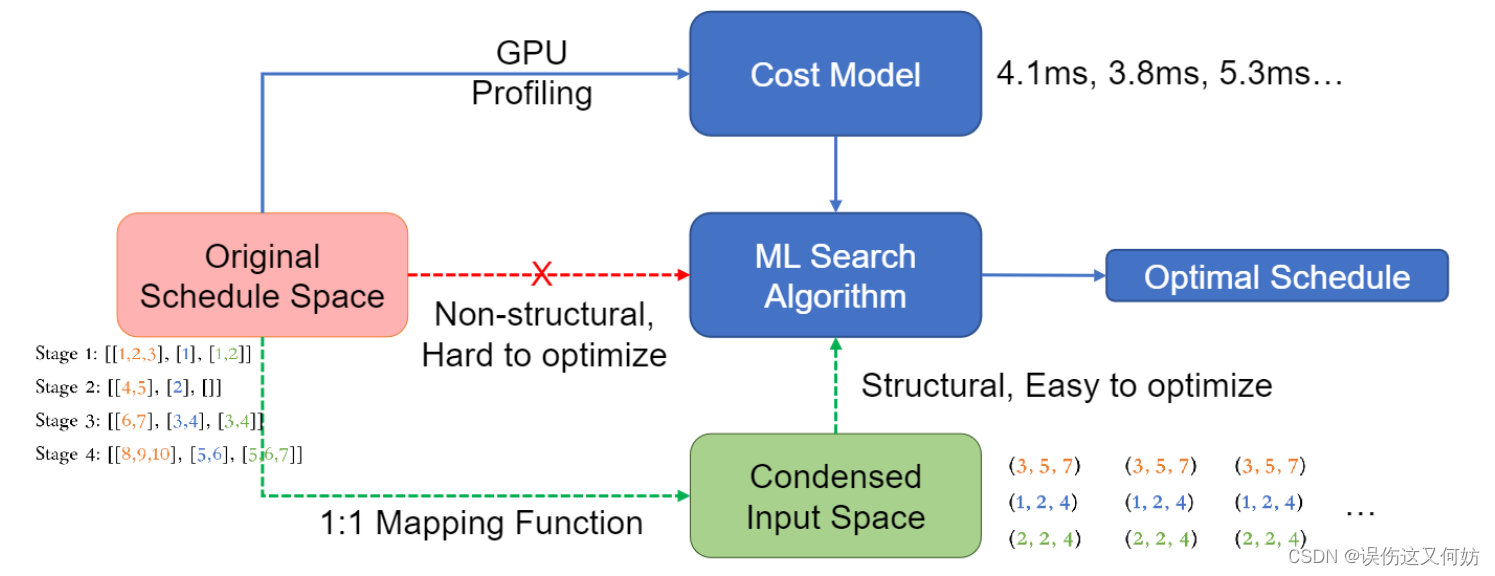
首先要明确我们的目标是找到一个stage集合，使得总时延最少。

$${\tau }^{?}=\arg \underset{\tau }{\min }f(\tau ),\text{for}\tau \in D_{\tau }$$
但由于 $D_{\tau }$ 并不是一个规则的数组集合，这导致难以比较和优化，在此，做了一个pointers和stages的映射：
$$\begin{array}{rl}& {\rho }^{?}=\arg \underset{\rho }{\min }f(\tau ),\\ & s.t.\tau =T(G,\rho ),\mathrm{for}\rho \in D_{\rho }.\end{array}$$
关于 $T(G,\rho )$ 的用法，下面这个例子可以说明：

$$\begin{array}{rl}{\rho }_1:(3,5,7)& +{\mathcal{S}}_1:[1,2,3,...,9,10]=\\ & {\mathcal{S}}_1^{{}^{\prime }}:[1,2,3],[4,5],[6,7],[8,9,10]\end{array}$$

这样我们可以将不定长且不规则的Stages数组变成规则的pointers矩阵。之后根据上图进行迭代优化，找出最优解。

Random Search

第一种方法是随机搜索，顾名思义，该算法会从搜索空间中随机抽取样本（pointers矩阵），然后计算相应的时延成本。经过多轮迭代，选择最低时延成本的样本作为最优解。

这种方法虽然很简单，但后面也验证了该方法的有效性。

Coordinate Gradient Search

第二种方法是坐标梯度搜素。这种方法类似于我们所说的控制变量法。核心思想是每次仅仅对一个模型的划分策略做优化。
具体的算法流程如下：

模型性能评估

加速性能

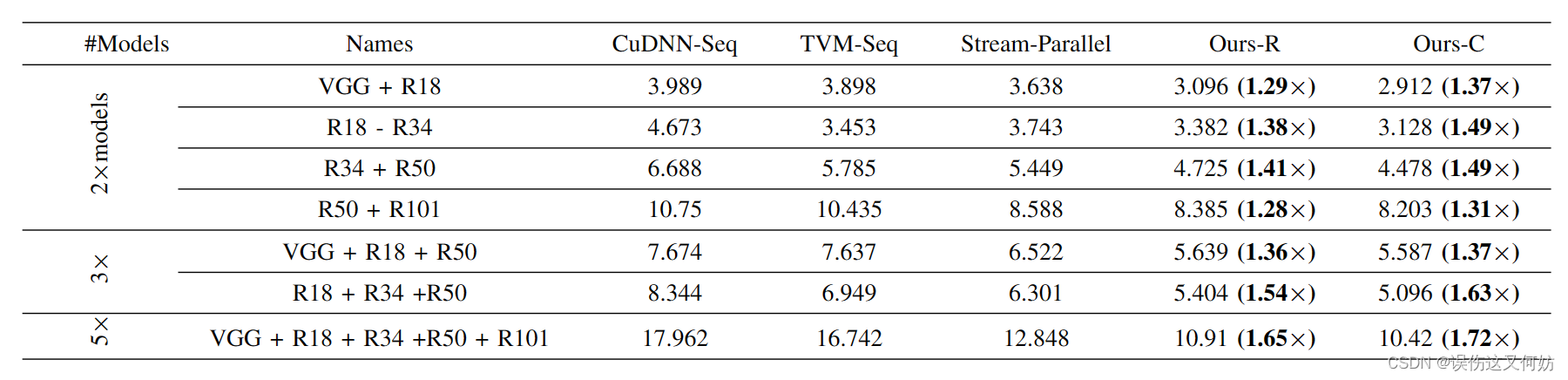
可以看到，该模型所用时间比传统算法都有提高，模型集合的复杂程度越高，性能越好。这其实也符合常理，不同模型复杂度相差越大，该算法的加速效率越高，因为它将资源更加均匀地分配了。

搜索算法比较与开销分析

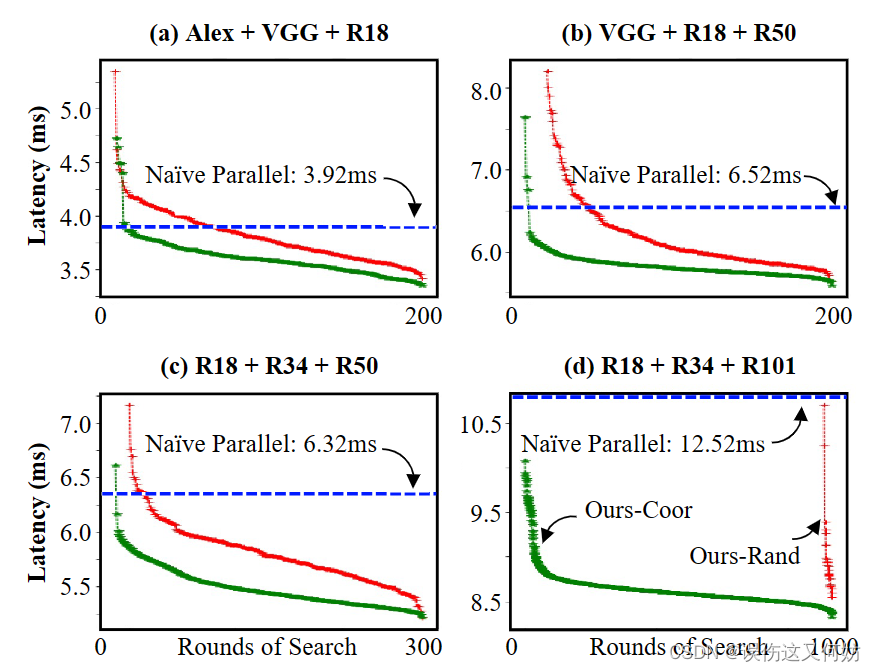
在所有情况下，无论是Random还是Coordinate都优于传统的并行策略。但在模型集合复杂度很高的时候，Random算法的效果并不理想，只有在1000轮时才有很明显的效果。话又说回来，如果模型集合的复杂度不高，大可以使用Random算法，这个算法的时间复杂度一定是远远低于coordinate算法的。

下面来看一下Coordiante算法的时间开销。

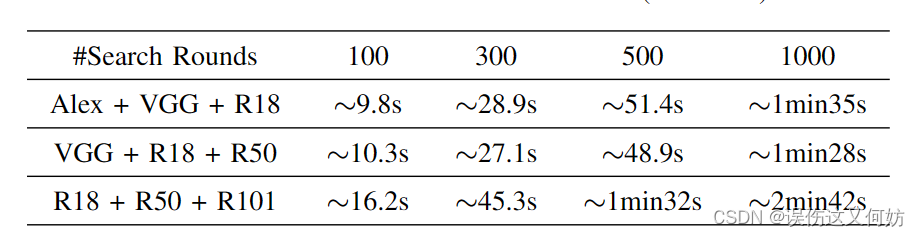
在大部分情况下，Coordiante算法的时间开销大概在10s-3min内。由于我们只需要对模型集合调整一次（但模型集合会有很多呀）并且可以离线调优，因此是这点时间开销可以接受的。