PyTorch官网demo解读——第一个神经网络（2）

上一篇：PyTorch官网demo解读——第一个神经网络（1）

继上一篇文章我们展示了第一个神经网络的完整代码，今天我们来聊聊这个神经网络的模型设计。

这个demo实际上只使用了一个简单的线性模型：y = wx + b；

手写数字识别最后其实只输出10个结果（0~9），所以我们可以将结果表示为包含十个数的一维矩阵?[10]，矩阵中的每个值是预测的概率值，表示索引代表的数字的概率。

我们的图片是28*28=784像素的，我们用一维矩阵[784]来表示，所以我们的目标就是将784 => 10。因为这个demo中只使用了一层神经网络，于是我们将我们的权重参数设计成784x10的二维矩阵[784, 10]，这样每张图片的像素值乘以权重矩阵就得出10个数的一维矩阵[10]，再加上10个数的偏差值bias就是我们预测的结果了。是不是很简单:=))

每个权重参数其实就是一个神经元，那么我们总共只使用了7840个神经元，就可以识别数字了。

每个神经元执行的计算也很简单，就是进行了一次 y = wx + b 的函数运算，结果y再进行一次激活函数运算（log_softmax）

模型运行简化流程如下图：

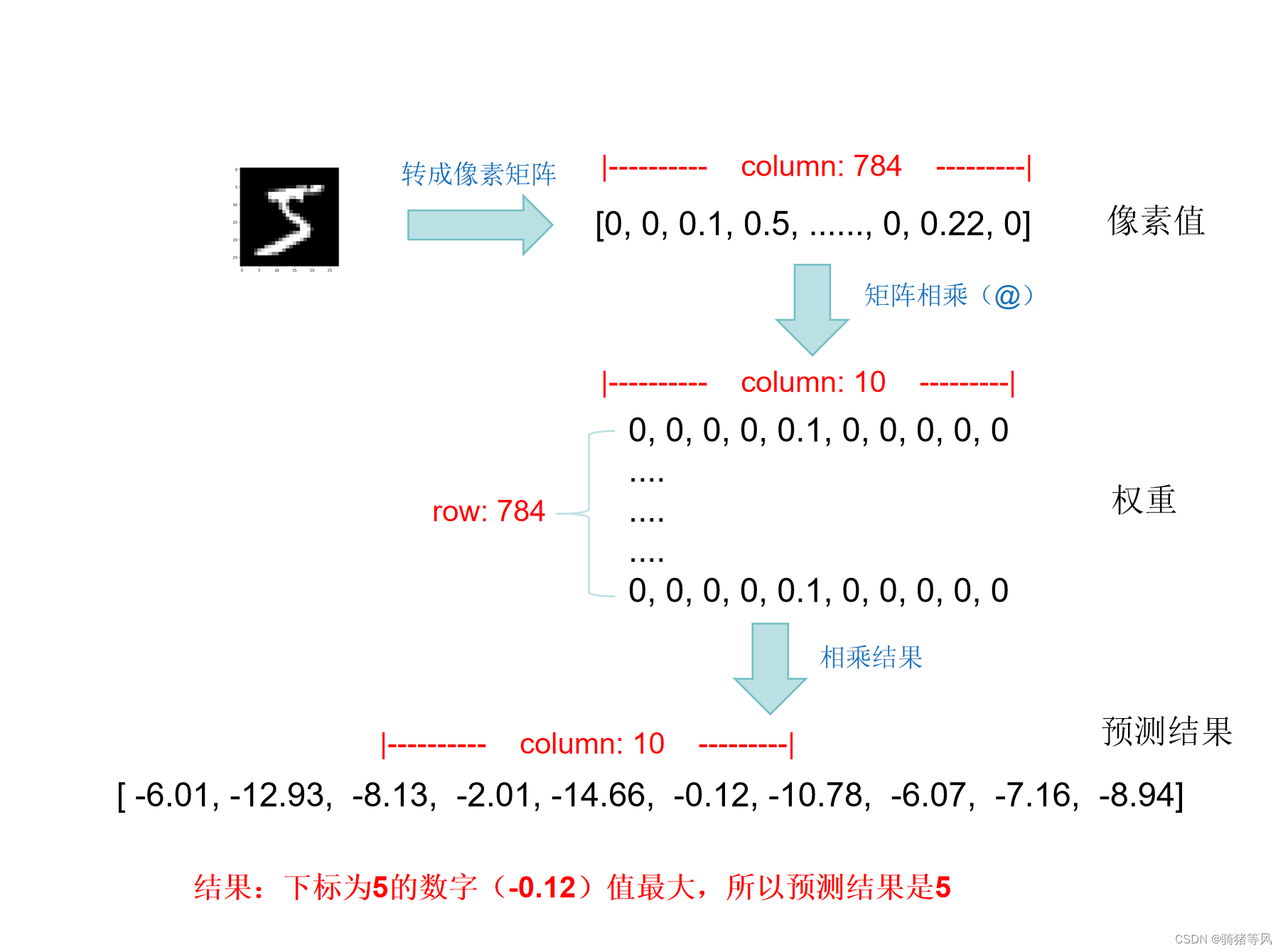
对应demo中的关键代码：

# 初始化权重和偏差值，权重是随机出来的784*10的矩阵，偏差初始化为0
weights = torch.randn(784, 10) / math.sqrt(784)
weights.requires_grad_()
bias = torch.zeros(10, requires_grad=True)

# 激活函数
def log_softmax(x):
    return x - x.exp().sum(-1).log().unsqueeze(-1)

# 定义模型：y = wx + b
# 实际上就是单层的Linear模型
def model(xb):
    return log_softmax(xb @ weights + bias)

ok，今天就先聊到这里吧！

原来数学如此的美，代码的尽头是数学？