【Python可视化系列】一文教你绘制不同类型的散点图（理论+源码）

一、引言

前文相关回顾：

【Python可视化系列】一文教会你绘制美观的热力图（理论+源码）

【Python可视化系列】一文教会你绘制美观的直方图（理论+源码）

【Python可视化系列】一文教会你绘制美观的柱状图（理论+源码）

【Python可视化系列】一文彻底教会你绘制美观的折线图（理论+源码）? ??

? ? ? ?本文将总结一下散点图的绘制方法。散点图也叫 X-Y 图，它将所有的数据以点的形式展现在直角坐标系上，以显示变量之间的相互影响程度，点的位置由变量的数值决定。

? ? ? ?通过观察散点图上数据点的分布情况，我们可以推断出变量间的相关性。如果变量之间不存在相互关系，那么在散点图上就会表现为随机分布的离散的点，如果存在某种相关性，那么大部分的数据点就会相对密集并以某种趋势呈现。数据的相关关系主要分为：正相关（两个变量值同时增长）、负相关（一个变量值增加另一个变量值下降）、不相关、线性相关、指数相关等。

二、参数详解

函数：
matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, , data=None, *kwargs)
参数说明
x, y : 相同长度的数组，数组大小(n，)，也就是绘制散点图的数据；
s：绘制点的大小，可以是实数或大小为(n，)的数组， 可选的参数 ；
c：绘制点颜色， 默认是蓝色'b' ， 可选的参数 ；
marker：表示的是标记的样式，默认的是'o' ， 可选的参数 ；
cmap：当c是一个浮点数数组的时候才使用， 可选的参数 ；
norm：将数据亮度转化到0-1之间，只有c是一个浮点数的数组的时候才使用， 可选的参数 ；
vmin , vmax：实数，当norm存在的时候忽略。用来进行亮度数据的归一化 ， 可选的参数 ；
alpha：实数，0-1之间， 可选的参数 ；
linewidths：标记点的长度， 可选的参数 ；

三、实现过程

3.1 基本散点图

data = pd.read_csv(r'Dataset.csv')
df = pd.DataFrame(data)

sns.set(font_scale=1.2)
plt.rc('font',family=['Times New Roman', 'SimSun'], size=12)
plt.scatter(df['age'], df['chol'])
plt.title('age与chol的关系')
plt.xlabel('age')
plt.ylabel('chol')
plt.show()

基本散点图也叫 X-Y 图，它将所有的数据以点的形式展现在直角坐标系上，以显示变量之间的相互影响程度，点的位置由变量的数值决定。

3.2 分组散点图

data = pd.read_csv(r'Dataset.csv')
df = pd.DataFrame(data)
colors = ['red','blue']
target = df['target'].unique()

sns.set(font_scale=1.2)
plt.rc('font',family=['Times New Roman', 'SimSun'], size=12)
for i in range(len(target)):
    plt.scatter(df.loc[df.target == i, 'age'], df.loc[df.target==i,'chol'], s = 35, c = colors[i], label = i)
plt.title('age与chol的关系')
plt.xlabel('age')
plt.ylabel('chol')
plt.legend(loc='upper left')# 默认是左上方，
plt.show()

分组分类散点图是在两个主特征的基础上，叠加一个分类特征。

3.3 气泡图

data = pd.read_csv(r'Dataset.csv')
df = pd.DataFrame(data)
# 假设thalach的第三个特征展示为为气泡大小
fea = df['thalach']
plt.scatter(df['age'], df['chol'], s=fea/2, c='purple', alpha=0.4, edgecolors="grey",
            linewidth=2)
plt.xlabel('age')  # 横坐标轴标题
plt.ylabel('chol')  # 纵坐标轴标题
plt.title('s=thalach/2, c=purple', verticalalignment='bottom')
plt.show()
# 参数说明
# s：表征气泡大小的变量
# c：颜色，若想要彩色气泡，可以给c赋值，如c=fea
# alpha：不透明度
# edgecolors：气泡描边的颜色
# linewidth：气泡描边大小

气泡图的其中一条变量的表现形式是体现在气泡的大小或颜色深浅上，如果一个数据集中包含非常多的点，那么散点图可以将这些数据对比的结果一目了然，是比较适用的。分组分类散点图是在两个主特征的基础上，叠加一个分类特征，若在两个主特征的基础上，还要展示另外一个连续特征，可以使用气泡图。

3.4 三维散点图

data = pd.read_csv(r'Dataset.csv')
df = pd.DataFrame(data)

sns.set(font_scale=1.2)
plt.rc('font',family=['Times New Roman', 'SimSun'], size=12)
ax = plt.subplot(projection = '3d')  # 创建一个三维的绘图工程
ax.scatter(df['age'], df['chol'], df['thalach'])
plt.show()

三维散点图可以反映三个数值之间的关系，他是一个立体的图形，我们可以理解为将气泡图的三维数据绘制到三维坐标系，就形成了三维散点图。

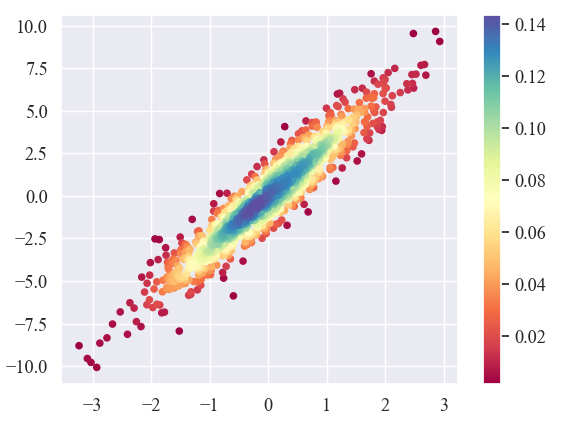
3.5 散点密度图

# 生成模拟数据
N=1000
x = np.random.normal(size=N)
y = x * 3 + np.random.normal(size=N)

# 计算样本点密度
xy = np.vstack([x,y])  #  将两个维度的数据叠加
z = gaussian_kde(xy)(xy)  # 建立概率密度分布，并计算每个样本点的概率密度

# 按密度排序，将密度最大的点排在最后
idx = z.argsort()
x, y, z = x[idx], y[idx], z[idx]
sns.set(font_scale=1.2)
plt.rc('font',family=['Times New Roman', 'SimSun'], size=12)
fig, ax = plt.subplots()
plt.scatter(x, y,c=z, s=20,cmap='Spectral') # c表示标记的颜色
plt.colorbar()
plt.show()

散点密度主要是计算样本点的出现次数，即密度。

本期内容就到这里，我们下期再见！需要数据集和源码的小伙伴可以关注底部公众号添加作者微信！

作者简介：

读研期间发表6篇SCI数据挖掘相关论文，现在某研究院从事数据算法相关科研工作，结合自身科研实践经历不定期分享关于Python、机器学习、深度学习、人工智能系列基础知识与应用案例。致力于只做原创，以最简单的方式理解和学习，关注我一起交流成长。