ID3决策树的建模流程

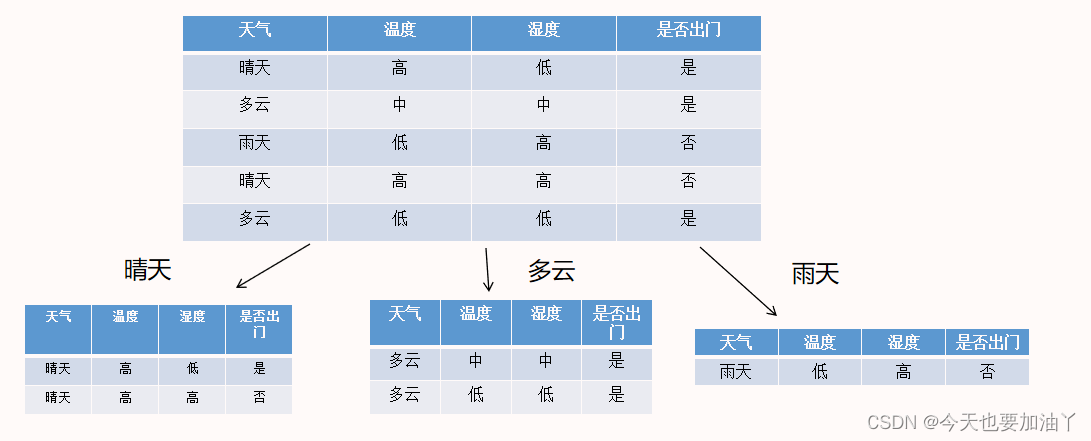
下面以一个简单的数据集，包括了天气、温度、湿度三个特征，以及是否出门的目标变量，来演示ID3决策树的建模流程。

天气	温度	湿度	是否出门
晴天	高	低	是
多云	中	中	是
雨天	低	高	否
晴天	高	高	否
多云	低	低	是

CART树是按照某切分点来展开，而ID3则是按照列来展开，即根据某列的不同取值来对数据集进行划分。

以天气的不同取值为划分规则

首先计算父节点的信息熵

为了表示方便，[2,3]表示[否的数量，是的数量]

entropy([2,3]) = $?\frac{2}{5}?lo{g}_2\frac{2}{5}?\frac{3}{5}?lo{g}_2\frac{3}{5}=0.97$

然后计算每个子节点的信息熵

以天气的不同取值为划分规则：

天气=晴天时
entropy([1,1]) = $?\frac{1}{2}?lo{g}_2\frac{1}{2}?\frac{1}{2}?lo{g}_2\frac{1}{2}=1$

天气=多云时
entropy([0,2]) = 0

天气=雨天时
entropy([1,0]) = 0

子节点的信息熵加权平均和为：（权重就是各子节点数据集数量占父节点数量）

entropy([1,1],[0,2],[1,0]) = $\frac{2}{5}$*entropy([1,1]) + $\frac{2}{5}$*entropy([0,2])+$\frac{1}{5}$*entropy([1,0])]= $\frac{2}{5}$*1 + $\frac{2}{5}$*0+$\frac{1}{5}$*0=0.4

基于天气判断是否出行的信息增益为gain(天气） = 0.97-0.4= 0.5

以温度的不同取值为划分规则：

温度=高时
entropy([1,1]) = $?\frac{1}{2}?lo{g}_2\frac{1}{2}?\frac{1}{2}?lo{g}_2\frac{1}{2}=1$

温度=中时
entropy([0,1]) = 0

温度=低时
entropy([1,1]) = 1

子节点的信息熵加权平均和为：

entropy([1,1],[0,1],[1,1]) = $\frac{2}{5}$*entropy([1,1]) + $\frac{1}{5}$*entropy([0,1])+$\frac{2}{5}$*entropy([1,1])]= $\frac{2}{5}$*1 + $\frac{1}{5}$*0+$\frac{2}{5}$*1=0.8

基于温度判断是否出行的信息增益为gain(天气） = 0.97-0.8= 0.17

以湿度的不同取值为划分规则：

湿度=高时
entropy([2,0]) = 0

湿度=中时
entropy([0,1]) = 0

湿度=低时
entropy([0,2]) =0

子节点的信息熵加权平均和为：

entropy([2,0],[0,1],[0,2]) = $\frac{2}{5}$*entropy([2,0]) + $\frac{1}{5}$*entropy([0,1])+$\frac{2}{5}$*entropy([0,2])]= $\frac{2}{5}$*0 + $\frac{1}{5}$*0+$\frac{2}{5}$*0=0

基于湿度判断是否出行的信息增益为gain(天气） = 0.97-0 = 0.97

选择信息增益最大的为划分规则，即以湿度为划分节点。

Notes:
(1) ID3树根据列来提取规则，每次展开一列会产生分支数量取决于当前列的分类水平，而CART树则只能生成二叉树。

(2) 由于ID3每次展开一列，建模过程中对列的消耗很快，树的最大深度取决于数据集中的特征个数，而CART树则具有更多备选规则，能够提取更精细的规则。

(3) ID3只能处理特征都是离散变量的数据集。此外，ID3更倾向于选择取值较多的分类变量展开，容易导致过拟合，且缺乏防止过拟合的措施，而这些缺陷正是C4.5算法改进的方向。