MIT_线性代数笔记:第 22 讲 对角化和矩阵的幂
目录
本讲中将学习如何对角化含有 n 个线性无关特征向量的矩阵,以及对角化是怎样简化计算的。
对角化矩阵 Diagonalizing a matrix S?1AS = Λ
如果矩阵 A 具有 n 个线性无关的特征向量,将它们作为列向量可以组成一个可逆方阵 S,并且有:
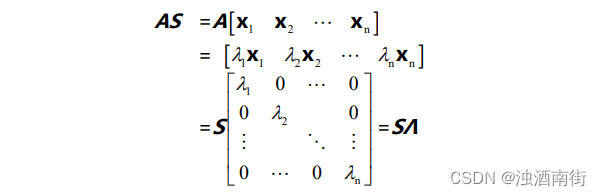
这里的矩阵 Λ 为对角阵,它的非零元素就是矩阵 A 的特征值。因为矩阵 S 中的列向量线性无关,因此逆矩阵 S-1存在。在等式两侧左乘逆矩阵,得到 S-1AS=Λ。同样地,A=SΛS-1。
对于消元法而言,矩阵有 LU 分解,对于施密特正交法,矩阵有 QR 分解,而上面的推导是一种新的矩阵分解。
矩阵的幂 Powers of A
特征值给矩阵的幂计算提供了方法。
如果 Ax=λx,则有
A
2
A^2
A2x=λAx=
λ
2
λ^2
λ2x。说明矩阵
A
2
A^2
A2 有着和 A 一样的特征向量,而特征值为
λ
2
λ^2
λ2。我们将写成对角化形式则有:
A
2
A^2
A2=SΛ
S
?
1
S^{-1}
S?1SΛ
S
?
1
S^{-1}
S?1=S
Λ
2
Λ^2
Λ2
S
?
1
S^{-1}
S?1。做相同的处理还可以得到:
A
k
A^k
Ak =S
Λ
k
Λ^k
Λk
S
?
1
S^{-1}
S?1。这说明
A
k
A^k
Ak 有着和 A 一样的特征向量,而特征值为
λ
k
λ^k
λk。
如果矩阵 A 具有 n 个线性无关的特征向量,如果所有的特征值均满足 ∣ λ i ∣ \begin{vmatrix} λ_i \end{vmatrix} ?λi?? ? <1 。则 k→∞时, A k A^k Ak→0。
重特征值 Repeated eigenvalues
如果矩阵 A 没有重特征值,则其一定具有 n 个线性无关的特征向量。
如果矩阵 A 有重特征值,它有可能具有 n 个线性无关的特征向量,也可能没有。比如单位阵的特征值为重特征值 1,但是其具有 n 个线性无关的特征向量。

差分方程 Difference equations u k + 1 u_{k+1} uk+1?=A u k u_k uk?
从给定的一个向量 u0 出发,我们可以通过对前一项乘以矩阵 A 得到下一项的方式,得到一个向量序列: u k + 1 u_{k+1} uk+1?=A u k u_k uk?.
这里的
u
k
+
1
u_{k+1}
uk+1?=A
u
k
u_k
uk?可以是一个一阶差分方程,而
u
k
u_k
uk?=
A
k
u
0
A^ku_0
Aku0?就是方程的解。但这种简洁形式并没有给出足够的信息,我们需要通过特征向量和矩阵的幂运算给出真实解的结构。

斐波那契数列 Fibonacci sequence
斐波那契数列为 0,1,1,2,3,5,8,13……其通项公式为 Fk+2=Fk+1+Fk。求 F100 ? 如果我们以矩阵的方式来理解数列,则矩阵的特征值可以告诉我们数列中数值的增长速度。
为了凑成矩阵形式,需要用一个比较巧妙的技巧。令
u
k
u_k
uk? =
[
a
b
]
\begin{bmatrix} a\\b \end{bmatrix}
[ab?] ,则有:
F
k
+
2
=
F
k
+
1
+
F
k
F
k
+
1
=
F
k
+
1
\begin{align*} &F_{k+2} = F_{k+1} + F_{k}\\ &F_{k+1} = F_{k+1} \end{align*}
?Fk+2?=Fk+1?+Fk?Fk+1?=Fk+1??
写成矩阵形式为
u
k
+
1
=
[
1
1
1
0
]
u
k
u_{k+1} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} u_k
uk+1?=[11?10?]uk?
观察矩阵 A=
[
1
1
1
0
]
\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}
[11?10?]的特征值和特征向量,因为其为对称矩阵,特征值为实数,且特征向量正交。

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【状态估计】观测信号(包括异常值)的状态估计方法(Matlab代码实现)
- 学习vue3(一)
- python学生信息管理系统(界面+数据库)
- ArkTS语言基础入门学习-鸿蒙开发
- AI智能分析网关V4烟火检测算法解决方案
- 2024年Google Ads新手指南——广告运作与类型、工具
- 数据结构OJ实验1-顺序表
- C中数组名代表首元素地址的两个例外
- Qt中使用OpenGL的三种方式
- 计算机毕业设计—SSM酒店管理系统(附源码)