机器学习——决策树(一)
【说明】文章内容来自《机器学习——基于sklearn》,用于学习记录。若有争议联系删除。
1、简介
????????决策树(decision tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于或等干0的概率,用以评价项且风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称为决策树。决策树是一种非常常见并且优秀的机器学习算法,它易于理解、可解释性强,其可用于分类算法,也可用于回归模型。
????????决策树将算法组织成一棵树的形式。其实这就是将平时所说的if-then语句构建成了树的形式。这棵决策树主要包括3部分:内部节点、叶节点和边。内部节点是划分的属性,边表示划分的条件,叶节点表示类别。构建决策树就是一个递归地选择内部节点,计算划分条件的边,最后到达叶子节点的过程。

1.1 特点
优点:
- 推理过程容易理解,计算简单,可解释性强。
- 比较适合处理有缺失属性的样本。
- 可自动忽略目标变量没有贡献的属性变量,也为判断属性变量的重要性,减少变量的数目提供参考。
缺点:
- 容易造成过拟合,需要采用剪枝操作。
- 忽略了数据之间的相关性。
- 对于各类别样本数量不一致的数据,信息增益会偏向于那些更多数值的特征。
1.2 示例
根据客户的职业、收入、年龄以及学历等信息判断客户是否有贷款意向。
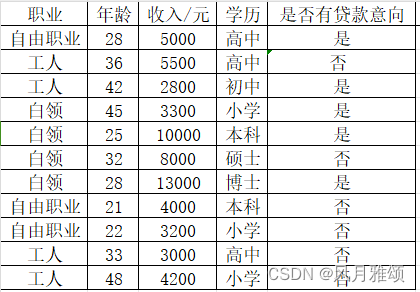
客户信息表示为{职业,年龄,收入,学历}。某客户信息为{工人,39,1800,小学},决策树的决策步骤如下:
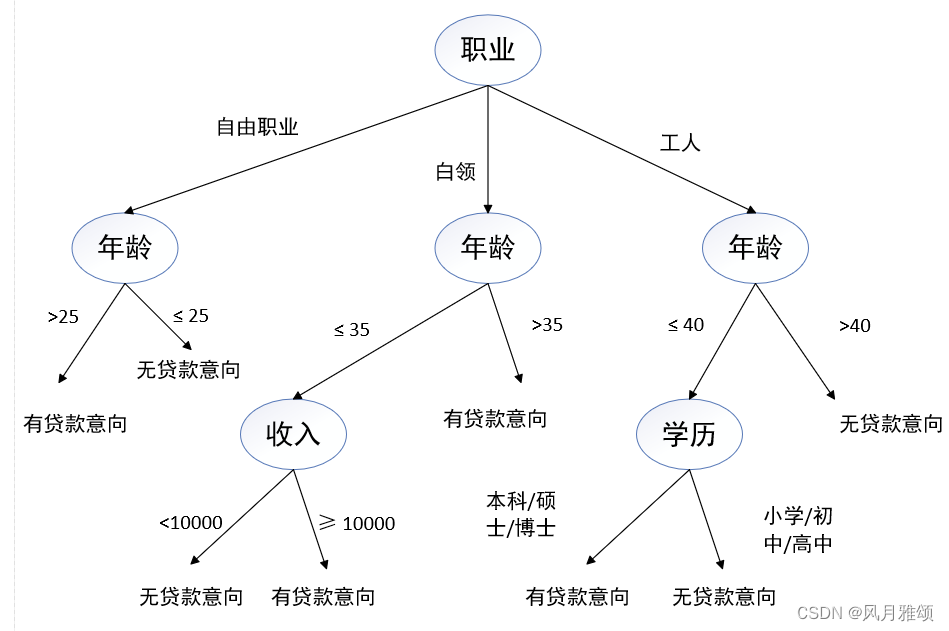
最终得出该客户无贷款意向。可以看出,属性选择的先后次序对于构造决策树有至关重要的作用。
2、决策树相关概念
2.1 信息
????????信息泛指在社会中传播的一切内容,包括音讯、消息、通信系统传输和处理的对象等。信息可以通过信息熵被量化。1948年,香农在《通信的数学原理》这篇论文中指出:“信息是用来消除随机不确定性的东西。”
2.2 信息熵
????????信息熵是表示信息含量的指标。越不确定的事件,其信息熵越大。信息熵的计算公式如下:
其中P(x)表示事件x出现的概率,X是事件全体的集合。
信息熵性质:
- 单调性。发生概率越高的事件,信息熵越低。例如,“太阳从东方升起”是确定事件,没有消除任何不确定性,所以不携带任何信息量。
- 非负性。信息熵不能为负。
- 累加性。多个事件总的信息熵等于各个事件的信息熵之和。
2.3 互信息
????????互信息是对两个离散型随机变量X和Y相关程度的度量,互信息的维恩图如图所示,左圆圈表示X的信息熵H(X),右圆圈表示Y的信息熵H(Y),并集是联合分布的信息熵H(X,Y),差集是条件熵H(X|Y)或H(Y|X),交集为互信息I(X,Y)。互信息越大,意味着两个随机变量的关联就越密切。
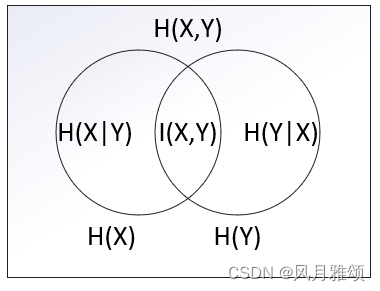
2.4 信息增益
????????决策树在划分数据集时选择信息熵变化最大的特征作为分类依据,也就是选择信息增益最大的特征作为分裂节点。不同的特征具有不同的信息增益,信息增益大的特征具有更强的分类能力。信息增益用g表示,其计算公式如下:
其中,条件熵H(X|A)是指在已知随机变量A的条件下X的不确定性。
3、决策树算法
决策树创建过程分为以下几步:
- 计算数据集划分前的信息熵。
- 遍历所有条件的特征,分别计算用每个特征划分数据集的信息熵。
- 选择信息增益最大的特征作为数据划分节点。
- 递归地处理被划分后的数据集,当满足信息增益的阚值时,结束递归。
决策树的典型算法有ID3.C4.5和 CART等。
3.1 ID3算法
????????ID3(Iterative Dichotomiser 3,迭代二叉树3代)是一种贪心算法,以信息论为基础,以信息熵和信息增益作为衡量标准,对数据进行分类。ID3算法具有构建速度快、实现简单等优点。ID3算法有如下缺点:
- 依赖于数目较多的特征。
- 不是递增算法
- 不考虑特征属性之间的关系。
- 抗噪性差。
- 只适合小规模数据集。
3.2?C4.5算法
?C4.5算法继承了1D3算法的优点,并在以下几方面进行了改进:
- 弥补了信息增益选择偏向取值多的特征的缺陷。
- 在决策树构造过程中进行剪枝操作。
- 能够对连续属性进行离散化处理。
- 能够对不完整数据进行处理,
C4.5算法需对数据集进行多次顺序扫描和排序,因此该算法的效率较低。
3.3 CART算法
????????ID3算法和 C4.5 算法生成的决策树规模较大。为了提高生成决策树的效率,出现了CART(Classification And Regression Tree,分类和回归树)算法。当叶子节点是连续型数据时,该决策树为回归树;当叶子节点是离散型数据时,该决策树为分类树。CART 根据基尼系数选择测试属性,数据集D的基尼系数 Gini(D)的计算公式如下:
????????Gini(D)反映了从数据集D中随机抽到两个不一致类别的样本的概率。Gini(D)越小,数据集D的纯度越高;反之,纯度越低。
ID3.C4.5和 CART这3种算法的比较如下:
- ID3 和 C4.5算法均只适合在小规模数据集上使用。
- ID3 和 C4.5算法构建的都是单变量决策树。
- 当属性值较多时,C4.5算法效果较好,而ID3算法效果较差。
- 三者划分依据不同:ID3为信息增益,C4.5为信息增益率,CART为基尼系数和均方差。
- CART算法构建的决策树一定是二叉树,ID3 和 C4.5构建的决策树不一定是二叉树。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【Python】使用tkinter设计开发Windows桌面程序记事本(4)
- JavaScript 中常用事件
- leetcode9.回文数java解法
- 2024.Python
- OWASP ZAP:下一代网络安全的瑞士军刀
- Mac上修复Gitee报错 Oauth: Access token is expired
- 【稳定检索、投稿优惠】2024年电子电气工程与机械应用国际会议(ICEEEMA 2024)
- JDK安装与配置教程来啦
- 部署tomcat单机多实例,keepalived+mysql的互为主从高可用,mysql+keepalived高可用
- FlinkAPI开发之窗口(Window)