【图形学】探秘图形学奥秘：图形变换的解密与实战

发布时间：2024年01月15日

?🌈个人主页：Sarapines Programmer
🔥?系列专栏：《图形学 | 图像解码》
?诗赋清音：云生高巅梦远游， 星光点缀碧海愁。 山川深邃情难晤， 剑气凌云志自修。

?

目录

🌌1. 初识模式识别

🌌2.?图形变换

🌍2.1 开发环境及实现

🌍2.2 实验目的

🌍2.3 实验要求

🌍2.4 实验原理

🌍2.5 实验步骤

🌕2.5.1?平移变换

🌕2.5.2?旋转变换

🌕2.5.3?对称变换

🌕2.5.4?比例变换

🌍2.4 研究体会

📝总结

🌌1. 初识模式识别

图形学技术是一门涉及计算机图形和图像处理的学科，其目标是通过算法和数学模型来创建、处理和呈现图形和图像。这项技术的应用范围非常广泛，涵盖了许多领域，包括计算机游戏、虚拟现实、计算机辅助设计（CAD）、医学图像处理、动画制作等。

以下是图形学技术的一些关键方面：

  1. 图形生成和渲染： 图形学技术用于生成和呈现视觉图像。这包括三维图形的创建、光照、阴影、颜色和纹理等方面的处理，以产生逼真的图形。

  2. 计算机辅助设计（CAD）： 在工程学和设计领域，图形学技术被广泛用于创建和编辑数字化的设计图纸，促进设计过程的可视化和交互。

  3. 计算机游戏和虚拟现实： 图形学技术是游戏开发和虚拟现实领域的核心。它用于创建游戏中的角色、场景、特效以及虚拟现实环境，提供沉浸式的视觉体验。

  4. 医学图像处理： 在医学领域，图形学技术被用于处理和呈现医学图像，如CT扫描、MRI等，以协助医生进行诊断和手术规划。

  5. 动画制作： 图形学技术是制作动画的关键。通过在计算机上生成图形帧并进行渲染，动画制作得以实现。

  6. 图像处理： 图形学技术也包括对静态图像的处理，如图像编辑、滤镜应用、图像合成等。

在图形学技术的发展中，硬件加速、实时渲染、虚拟现实和增强现实等方面的创新不断推动着图形学的前沿。这门技术为数字世界的可视化和交互提供了强大的工具和方法。

🌌2.?图形变换

🌍2.1 开发环境及实现

  • 语言: C++
  • 平台: Microsoft Visual Studio 2022

🌍2.2 实验目的

  • 进行二维图形的各种几何变换，利用基本图形实现。

🌍2.3 实验要求

  1. 使用Microsoft Visual Studio 2022编程。
  2. 实现以下几何变换：
    • 平移变换
    • 旋转变换
    • 对称变换
    • 比例变换。

🌍2.4 实验原理

图形的几何变换一般是指对图形的几何信息经过变换后产生新的图形，图形几何变换既可以看作是坐标系不动而图形变动，变动后的图形在坐标系中的坐标值发生变化；出可以看作图形不动而坐标系变动，变动后的图形在新坐标系下具有新的坐标值。这两种情况本质上都是一样的，都是图形由新的坐标值表示，因此是新产生的图形。图形几何变换包括比例变换、对称变换、错切变换、旋转变换、平移变换及其复合变换。图形上所有的点在几何变换前后的坐标关系一般用解析几何方法可以求得，但这些几何关系用矩阵方法表示，运算更为方便。

图形基本几何变换是指比例变换、对称变换、错切变换、旋转变换和平移变换等。除平移变换外，这里其它四种几何变换都可以用组成图形的点向量(或称1×2阶矩阵)和2×2阶变换矩阵相乘表示，而平移变换需引入新方法来实现。

🌍2.5 实验步骤

对图形分别进行平移变换、旋转变换、对称变换以及比例变换。

程序代码示例如下：

🌕2.5.1?平移变换
#include <GL/glut.h>
#include <stdlib.h>
#include <math.h>

GLsizei winWidth = 600, winHeight = 600;
GLfloat xwcMin = 0.0, xwcMax = 225.0;
GLfloat ywcMin = 0.0, ywcMax = 225.0;

class wcPt2D
{
public:
	GLfloat x, y;
};

typedef GLfloat Matrix3x3[3][3];

Matrix3x3 matComposite;

const GLdouble pi = 3.14159;

void Init()
{
	glClearColor(1.0, 1.0, 1.0, 0.0);
}

void Matrix3x3SetIdentity(Matrix3x3 matIdent3x3)
{
	GLint row, col;

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			matIdent3x3[row][col] = (row == col);
		}
	}
}

void Matrix3x3PreMultiply(Matrix3x3 m1, Matrix3x3 m2)
{
	GLint row, col;
	Matrix3x3 matTemp;

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			matTemp[row][col] =
				m1[row][0] * m2[0][col] +
				m1[row][1] * m2[1][col] +
				m1[row][2] * m2[2][col];
		}
	}

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			m2[row][col] = matTemp[row][col];
		}
	}
}

void Translate2D(GLfloat tx, GLfloat ty)
{
	Matrix3x3 matTransl;
	Matrix3x3SetIdentity(matTransl);
	matTransl[0][2] = tx;
	matTransl[1][2] = ty;
	Matrix3x3PreMultiply(matTransl, matComposite);
}


void TransformVerts2D(GLint nVerts, wcPt2D* verts)//平移函数实现
{
	GLint k;
	GLfloat temp;

	for (k = 0; k < nVerts; k++)
	{
		temp = matComposite[0][0] * verts[k].x +
			matComposite[0][1] * verts[k].y +
			matComposite[0][2];

		verts[k].y = matComposite[1][0] * verts[k].x +
			matComposite[1][1] * verts[k].y +
			matComposite[1][2];
		verts[k].x = temp;
	}
}

void Trangle(wcPt2D* verts)
{
	GLint k;

	glBegin(GL_TRIANGLES);
	for (k = 0; k < 3; k++)
	{
		glVertex2f(verts[k].x, verts[k].y);
	}
	glEnd();
}

void WinReshapFcn(GLint newWidth, GLint newHeight)
{
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(xwcMin, xwcMax, ywcMin, ywcMax);

	glClear(GL_COLOR_BUFFER_BIT);
}

void DisplayFcn()
{
	glClear(GL_COLOR_BUFFER_BIT);
	GLint nVerts = 3;
	wcPt2D verts[3] = { {50,25},{150,25 },{100,100} };

	wcPt2D centroidPt;

	GLint k, xSum = 0, ySum = 0;

	for (size_t k = 0; k < nVerts; k++)
	{
		xSum += verts[k].x;
		ySum += verts[k].y;
	}

	centroidPt.x = GLfloat(xSum) / GLfloat(nVerts);
	centroidPt.y = GLfloat(ySum) / GLfloat(nVerts);

	wcPt2D pivPt, fixedPt;
	pivPt = centroidPt;
	fixedPt = centroidPt;

	GLfloat tx = 0, ty = 100;
	GLfloat sx = 0.5, sy = 0.5;
	GLdouble theta = pi / 2;
	glColor3f(0, 0, 1);
	Trangle(verts);
	Matrix3x3SetIdentity(matComposite);
	Translate2D(tx, ty);
	TransformVerts2D(nVerts, verts);//调用函数
	glColor3f(1, 0, 0);
	Trangle(verts);
	glFlush();
}

void draw_pixel(int ix, int iy)
{
	glBegin(GL_POINTS);
	glVertex2i(ix, iy);
	glEnd();
}

void myinit()
{
	glClearColor(1.0, 0.8, 1.0, 1.0);
	glColor3f(0.0, 0.5, 0.5);
	glPointSize(1.0);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0.0, 1000.0, 0.0, 1000.0);
}
int main(int argc, char** argv)
{
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowSize(600, 500);
	glutInitWindowPosition(150.0, 150.0);
	glutCreateWindow("图像平移变换");
	glutDisplayFunc(DisplayFcn);
	glutReshapeFunc(WinReshapFcn);
	myinit();
	glutMainLoop();
}

运行结果：

?

🌕2.5.2?旋转变换
#include <GL/glut.h>
#include <stdlib.h>
#include <math.h>

GLsizei winWidth = 600, winHeight = 600;

GLfloat xwcMin = 0.0, xwcMax = 225.0;
GLfloat ywcMin = 0.0, ywcMax = 225.0;

class wcPt2D
{
public:
	GLfloat x, y;
};

typedef GLfloat Matrix3x3[3][3];

Matrix3x3 matComposite;

const GLdouble pi = 3.14159;

void Init()
{
	glClearColor(1.0, 1.0, 1.0, 0.0);
}

void Matrix3x3SetIdentity(Matrix3x3 matIdent3x3)
{
	GLint row, col;

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			matIdent3x3[row][col] = (row == col);
		}
	}
}

void Matrix3x3PreMultiply(Matrix3x3 m1, Matrix3x3 m2)
{
	GLint row, col;
	Matrix3x3 matTemp;

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			matTemp[row][col] =
				m1[row][0] * m2[0][col] +
				m1[row][1] * m2[1][col] +
				m1[row][2] * m2[2][col];
		}
	}

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			m2[row][col] = matTemp[row][col];
		}
	}
}

void Translate2D(GLfloat tx, GLfloat ty)
{
	Matrix3x3 matTransl;

	Matrix3x3SetIdentity(matTransl);

	matTransl[0][2] = tx;
	matTransl[1][2] = ty;

	Matrix3x3PreMultiply(matTransl, matComposite);
}

void Rotate2D(wcPt2D pivotPt, GLfloat theta)//旋转
{
	Matrix3x3 matRot;

	Matrix3x3SetIdentity(matRot);

	matRot[0][0] = cos(theta);
	matRot[0][1] = -sin(theta);
	matRot[0][2] = pivotPt.x * (1 - cos(theta)) +
		pivotPt.y * sin(theta);

	matRot[1][0] = sin(theta);
	matRot[1][1] = cos(theta);
	matRot[1][2] = pivotPt.y * (1 - cos(theta)) -
		pivotPt.x * sin(theta);

	Matrix3x3PreMultiply(matRot, matComposite);
}

void TransformVerts2D(GLint nVerts, wcPt2D* verts)//平移
{
	GLint k;
	GLfloat temp;

	for (k = 0; k < nVerts; k++)
	{
		temp = matComposite[0][0] * verts[k].x +
			matComposite[0][1] * verts[k].y +
			matComposite[0][2];

		verts[k].y = matComposite[1][0] * verts[k].x +
			matComposite[1][1] * verts[k].y +
			matComposite[1][2];
		verts[k].x = temp;
	}
}

void Trangle(wcPt2D* verts)
{
	GLint k;

	glBegin(GL_TRIANGLES);
	for (k = 0; k < 3; k++)
	{
		glVertex2f(verts[k].x, verts[k].y);
	}
	glEnd();
}

void WinReshapFcn(GLint newWidth, GLint newHeight)
{
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(xwcMin, xwcMax, ywcMin, ywcMax);

	glClear(GL_COLOR_BUFFER_BIT);
}

void DisplayFcn()
{
	GLint nVerts = 3;
	wcPt2D verts[3] = { {50,25},{150,25 },{100,100} };

	wcPt2D centroidPt;

	GLint k, xSum = 0, ySum = 0;

	for (size_t k = 0; k < nVerts; k++)
	{
		xSum += verts[k].x;
		ySum += verts[k].y;
	}

	centroidPt.x = GLfloat(xSum) / GLfloat(nVerts);
	centroidPt.y = GLfloat(ySum) / GLfloat(nVerts);

	wcPt2D pivPt, fixedPt;
	pivPt = centroidPt;
	fixedPt = centroidPt;

	GLfloat tx = 0, ty = 100;
	GLfloat sx = 0.5, sy = 0.5;
	GLdouble theta = pi / 2;
	glClear(GL_COLOR_BUFFER_BIT);
	glColor3f(0, 0, 1);
	Trangle(verts);
	Matrix3x3SetIdentity(matComposite);
	Rotate2D(pivPt, theta);
	Translate2D(tx, ty);

	TransformVerts2D(nVerts, verts);

	glColor3f(1, 0, 0);
	Trangle(verts);

	glFlush();
}
void draw_pixel(int ix, int iy)
{
	glBegin(GL_POINTS);
	glVertex2i(ix, iy);
	glEnd();
}

void myinit()
{
	glClearColor(1.0, 0.8, 1.0, 1.0);
	glColor3f(0.0, 0.5, 0.5);
	glPointSize(1.0);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0.0, 1000.0, 0.0, 1000.0);
}
int main(int argc, char** argv)
{
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowSize(600, 500);
	glutInitWindowPosition(150.0, 150.0);
	glutCreateWindow("图像旋转变换");
	glutDisplayFunc(DisplayFcn);
	glutReshapeFunc(WinReshapFcn);
	myinit();
	glutMainLoop();
}

运行结果：

?

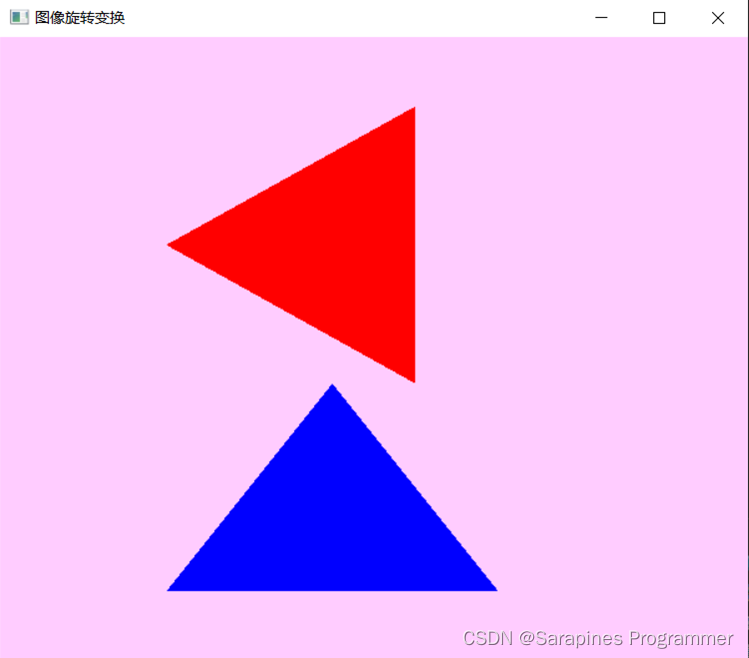
🌕2.5.3?对称变换
#include <GL/glut.h>
#include <stdlib.h>
#include <math.h>

GLsizei winWidth = 600, winHeight = 600;

GLfloat xwcMin = 0.0, xwcMax = 225.0;
GLfloat ywcMin = 0.0, ywcMax = 225.0;

class wcPt2D
{
public:
	GLfloat x, y;
};

typedef GLfloat Matrix3x3[3][3];

Matrix3x3 matComposite;

const GLdouble pi = 3.14159;

void Init()
{
	glClearColor(1.0, 1.0, 1.0, 0.0);
}

void Matrix3x3SetIdentity(Matrix3x3 matIdent3x3)
{
	GLint row, col;

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			matIdent3x3[row][col] = (row == col);
		}
	}
}

void Matrix3x3PreMultiply(Matrix3x3 m1, Matrix3x3 m2)
{
	GLint row, col;
	Matrix3x3 matTemp;

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			matTemp[row][col] =
				m1[row][0] * m2[0][col] +
				m1[row][1] * m2[1][col] +
				m1[row][2] * m2[2][col];
		}
	}

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			m2[row][col] = matTemp[row][col];
		}
	}
}

void Translate2D(GLfloat tx, GLfloat ty)
{
	Matrix3x3 matTransl;

	Matrix3x3SetIdentity(matTransl);

	matTransl[0][2] = tx;
	matTransl[1][2] = ty;

	Matrix3x3PreMultiply(matTransl, matComposite);
}

void Rotate2D(wcPt2D pivotPt, GLfloat theta)//旋转
{
	Matrix3x3 matRot;

	Matrix3x3SetIdentity(matRot);

	matRot[0][0] = cos(theta);
	matRot[0][1] = -sin(theta);
	matRot[0][2] = pivotPt.x * (1 - cos(theta)) +
		pivotPt.y * sin(theta);

	matRot[1][0] = sin(theta);
	matRot[1][1] = cos(theta);
	matRot[1][2] = pivotPt.y * (1 - cos(theta)) -
		pivotPt.x * sin(theta);

	Matrix3x3PreMultiply(matRot, matComposite);
}

void TransformVerts2D(GLint nVerts, wcPt2D* verts)//平移
{
	GLint k;
	GLfloat temp;

	for (k = 0; k < nVerts; k++)
	{
		temp = matComposite[0][0] * verts[k].x +
			matComposite[0][1] * verts[k].y +
			matComposite[0][2];

		verts[k].y = matComposite[1][0] * verts[k].x +
			matComposite[1][1] * verts[k].y +
			matComposite[1][2];
		verts[k].x = temp;
	}
}

void Trangle(wcPt2D* verts)
{
	GLint k;

	glBegin(GL_TRIANGLES);
	for (k = 0; k < 3; k++)
	{
		glVertex2f(verts[k].x, verts[k].y);
	}
	glEnd();
}

void WinReshapFcn(GLint newWidth, GLint newHeight)
{
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(xwcMin, xwcMax, ywcMin, ywcMax);

	glClear(GL_COLOR_BUFFER_BIT);
}

void DisplayFcn()
{
	GLint nVerts = 3;
	wcPt2D verts[3] = { {50,25},{150,25 },{100,100} };

	wcPt2D centroidPt;

	GLint k, xSum = 0, ySum = 0;

	for (size_t k = 0; k < nVerts; k++)
	{
		xSum += verts[k].x;
		ySum += verts[k].y;
	}

	centroidPt.x = GLfloat(xSum) / GLfloat(nVerts);
	centroidPt.y = GLfloat(ySum) / GLfloat(nVerts);

	wcPt2D pivPt, fixedPt;
	pivPt = centroidPt;
	fixedPt = centroidPt;

	GLfloat tx = 0, ty = 100;
	GLfloat sx = 0.5, sy = 0.5;
	GLdouble theta = pi;

	glClear(GL_COLOR_BUFFER_BIT);

	glColor3f(0, 0, 1);
	Trangle(verts);
	Matrix3x3SetIdentity(matComposite);
	Rotate2D(pivPt, theta);
	Translate2D(tx, ty);

	TransformVerts2D(nVerts, verts);

	glColor3f(1, 0, 0);
	Trangle(verts);

	glFlush();
}

void draw_pixel(int ix, int iy)
{
	glBegin(GL_POINTS);
	glVertex2i(ix, iy);
	glEnd();
}

void myinit()
{
	glClearColor(1.0, 0.8, 1.0, 1.0);
	glColor3f(0.0, 0.5, 0.5);
	glPointSize(1.0);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0.0, 1000.0, 0.0, 1000.0);
}
int main(int argc, char** argv)
{
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowSize(600, 500);
	glutInitWindowPosition(150.0, 150.0);
	glutCreateWindow("图像对称变换");
	glutDisplayFunc(DisplayFcn);
	glutReshapeFunc(WinReshapFcn);
	myinit();
	glutMainLoop();
}

运行结果：

?

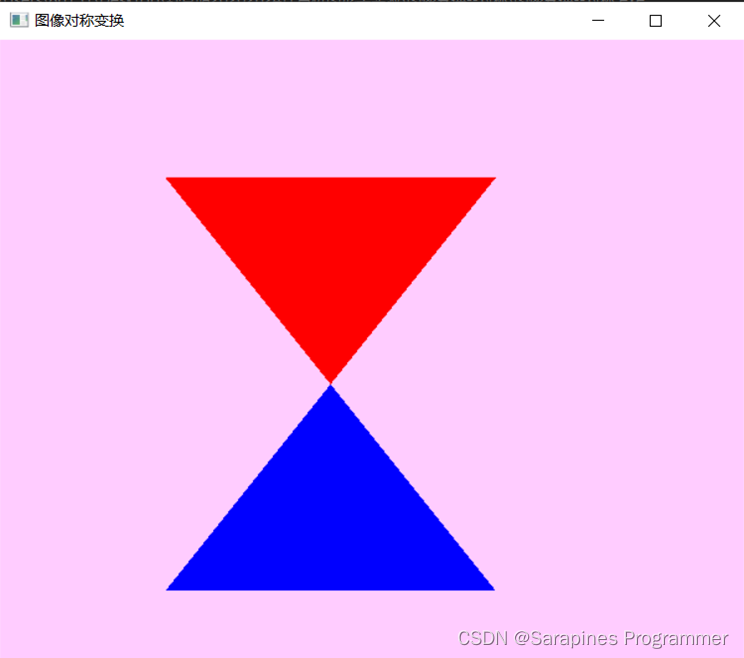🌕2.5.4?比例变换
#include <GL/glut.h>
#include <stdlib.h>
#include <math.h>

GLsizei winWidth = 600, winHeight = 600;

GLfloat xwcMin = 0.0, xwcMax = 225.0;
GLfloat ywcMin = 0.0, ywcMax = 225.0;

class wcPt2D
{
public:
	GLfloat x, y;
};

typedef GLfloat Matrix3x3[3][3];

Matrix3x3 matComposite;

const GLdouble pi = 3.14159;

void Init()
{
	glClearColor(1.0, 1.0, 1.0, 0.0);
}

void Matrix3x3SetIdentity(Matrix3x3 matIdent3x3)
{
	GLint row, col;

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			matIdent3x3[row][col] = (row == col);
		}
	}
}

void Matrix3x3PreMultiply(Matrix3x3 m1, Matrix3x3 m2)
{
	GLint row, col;
	Matrix3x3 matTemp;

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			matTemp[row][col] =
				m1[row][0] * m2[0][col] +
				m1[row][1] * m2[1][col] +
				m1[row][2] * m2[2][col];
		}
	}

	for (row = 0; row < 3; row++)
	{
		for (col = 0; col < 3; col++)
		{
			m2[row][col] = matTemp[row][col];
		}
	}
}

void Translate2D(GLfloat tx, GLfloat ty)
{
	Matrix3x3 matTransl;

	Matrix3x3SetIdentity(matTransl);

	matTransl[0][2] = tx;
	matTransl[1][2] = ty;

	Matrix3x3PreMultiply(matTransl, matComposite);
}

void Scale2D(GLfloat sx, GLfloat sy, wcPt2D fixedPt)//缩放
{
	Matrix3x3 matScale;

	Matrix3x3SetIdentity(matScale);

	matScale[0][0] = sx;
	matScale[0][2] = (1 - sx) * fixedPt.x;

	matScale[1][1] = sy;
	matScale[1][2] = (1 - sy) * fixedPt.y;

	Matrix3x3PreMultiply(matScale, matComposite);
}

void TransformVerts2D(GLint nVerts, wcPt2D* verts)//平移
{
	GLint k;
	GLfloat temp;

	for (k = 0; k < nVerts; k++)
	{
		temp = matComposite[0][0] * verts[k].x +
			matComposite[0][1] * verts[k].y +
			matComposite[0][2];

		verts[k].y = matComposite[1][0] * verts[k].x +
			matComposite[1][1] * verts[k].y +
			matComposite[1][2];
		verts[k].x = temp;
	}
}

void Trangle(wcPt2D* verts)
{
	GLint k;

	glBegin(GL_TRIANGLES);
	for (k = 0; k < 3; k++)
	{
		glVertex2f(verts[k].x, verts[k].y);
	}
	glEnd();
}

void WinReshapFcn(GLint newWidth, GLint newHeight)
{
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(xwcMin, xwcMax, ywcMin, ywcMax);

	glClear(GL_COLOR_BUFFER_BIT);
}

void DisplayFcn()
{
	GLint nVerts = 3;
	wcPt2D verts[3] = { {50,25},{150,25 },{100,100} };

	wcPt2D centroidPt;

	GLint k, xSum = 0, ySum = 0;

	for (size_t k = 0; k < nVerts; k++)
	{
		xSum += verts[k].x;
		ySum += verts[k].y;
	}

	centroidPt.x = GLfloat(xSum) / GLfloat(nVerts);
	centroidPt.y = GLfloat(ySum) / GLfloat(nVerts);

	wcPt2D pivPt, fixedPt;
	pivPt = centroidPt;
	fixedPt = centroidPt;

	GLfloat tx = 0, ty = 100;
	GLfloat sx = 0.5, sy = 0.5;
	GLdouble theta = pi / 2;

	glClear(GL_COLOR_BUFFER_BIT);

	glColor3f(0, 0, 1);
	Trangle(verts);

	Matrix3x3SetIdentity(matComposite);

	Scale2D(sx, sy, fixedPt);
	Translate2D(tx, ty);

	TransformVerts2D(nVerts, verts);

	glColor3f(1, 0, 0);
	Trangle(verts);

	glFlush();
}

void draw_pixel(int ix, int iy)
{
	glBegin(GL_POINTS);
	glVertex2i(ix, iy);
	glEnd();
}

void myinit()
{
	glClearColor(1.0, 0.8, 1.0, 1.0);
	glColor3f(0.0, 0.5, 0.5);
	glPointSize(1.0);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0.0, 1000.0, 0.0, 1000.0);
}
int main(int argc, char** argv)
{
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowSize(600, 500);
	glutInitWindowPosition(150.0, 150.0);
	glutCreateWindow("图像比例变换");
	glutDisplayFunc(DisplayFcn);
	glutReshapeFunc(WinReshapFcn);
	myinit();
	glutMainLoop();
}

运行结果：

?

🌍2.4 研究体会

  1. 实验内容完成： 通过本次实验，我成功地完成了图像平移、旋转、对称和比例缩放等变换操作。为了提高图像显示效果的清晰度，我在旋转、对称和缩放变换中添加了平移操作，以避免变换后的图像与原图重叠。这使我对图像变换操作有了深入的理解和实际操作经验。

  2. 自学与应用场景差距： 通过构造几何图像并进行变换操作，我意识到在实际应用场景中，通常是对给定的图像进行变换操作，而不是自己构造图像。虽然我在Python中对图像操作较为熟悉，但在C++中感觉到需要从头编写并控制每个功能。尽管这样的学习方式较为理想，但在实际应用中可能需要更多的库函数支持。

  3. 学习过程中的挑战和成就感： 实验中我花费了较多时间在图像生成的控制上，包括输出面板底色、图像初始位置和输出框大小等方面。由于之前主要在Dev-C++平台编程，初次使用Visual Studio 2022平台感到不太顺手，但通过自学和网上查找资料逐渐适应。最终看到运行结果时，感受到了付出的回报，同时也认识到在学习过程中需要保持耐心和专注。这次实验使我更加深入地了解了图形学，也激发了我对编程的热情和学习的动力。

📝总结

图形学领域宛如一片广阔而未被完全探索的创意海洋，邀请你勇敢踏足数字艺术和计算机图形学的神秘领域。这是一场富有创意和技术挑战的学习之旅，从基础概念到算法实现，逐步揭示更深层次的图形分析、渲染技术和智能图形识别的奥秘。渴望挑战图形学的学习路径和掌握计算机艺术的技能？不妨点击下方链接，一同探讨更多数字创意的奇迹吧。我们推出了引领趋势的💻 计算机图形学专栏：《艺术之光 | 数字创新解锁》，旨在深度探索图形学技术的实际应用和创新。🌐🎨

?

文章来源:https://blog.csdn.net/m0_57532432/article/details/135508078
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章