7.评价预测模型——C指数，NRI，IDI计算

发布时间：2024年01月17日

基本知识

1. C指数

2. NRI、IDI

基本知识

1. C指数

C指数：

C指数，又称为一致性指数，可评价模型的预测能力，尤其是评估COX回归模型的判别能力。C指数是指所有病人对子中，预测结果与实际结果一致的对子数占总子数的比例，表示预测结果与实际结果相一致的概率。

C指数的评价：

C指数的范围为0.5-1，若C指数为0.5，为完全随机，说明该模型没有预测作用；C指数为1，说明完全一致。C指数在0.5-0.7之间的精度较低，C指数在0.71-0.90之间为中等准确度，C指数在0.90以上为高准确度。

C-index与AUC的关系：

对于二元logistic回归模型，C指数可以简化为：预测患有某种疾病的患者出现疾病的概率大于预测该疾病本身的概率。结果表明，二元Logistic回归的C指数等价于AUC。AUC主要反映二元Logistic回归模型的预测能力，而C-index可以评价各种模型预测结果的准确性。

Cox模型的C指数计算概述：

（1）方法一：直接运用生存包中的coxph（）函数输出结果。95%CI可以通过C加减1.96*Se得到。

（2）方法二：在rms包中cph（）函数和validate（）函数，非调整的偏置调整的C-index都能得到。

2. NRI、IDI

净重新分类指数 NRI，综合判别改善指数 IDI可用于不同预测模型的比较。

C指数进行模型比较的缺点：

C指数不够敏感，在旧模型中增加新变量，C指数提升程度有限；
从临床角度，C指数不易被理解。

净重新分类改善指数（Net Reclassification Index，NRI）

原理：首先将研究对象按照金标准分为患病和未患病组，然后分别在这两组中，新、旧模型对研究对象进行分类，整理成两个四格表。最后根据患病组和未患病组中在新、旧模型下的差别来计算净重新分类指数NRI。

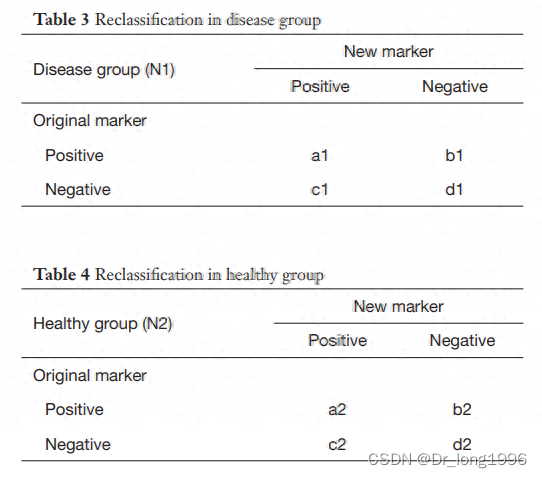
在table3中，c1是原来模型没有预测对，新模型预测对的，同样的道理，b1是原来模型预测对，但新模型给预测错的，于是(c1 ? b1)/N1便是疾病组或者event组增加的重分类的正确比。

同样我们可以得到非疾病组中（table 4）中增加的重分类正确比为(b2 ? c2)/N2。

NRI = (c1 ? b1)/N1 + (b2 ? c2)/N2

结果解读：NRI表示的是重分类的正确个案占比的增加量，所以若NRI>0，则为正改善，说明新模型比旧模型的预测能力有所改善；若NRI<0，则为负改善，新模型预测能力下降；若NRI=0，则认为新模型没有改善。

计算方法：预测模型NRI计算首选nricens包。

综合判别改善指数IDI（Integrated discrimination improvement, IDI）

原理：在疾病组，模型预测阳性的概率要尽可能大，在非疾病组模型预测阳性的概率要尽可能小，通过模型的预测概率差值依然可以得到一个评价指数。如果新模型比原模型：在阳性组，预测阳性的概率比旧模型的大；在阴性组，预测阳性的概率比旧模型的小。那么就可以说明新模型比旧模型好。

IDI = (Pnew,events–Pold,events) – (Pnew,non-events – Pold,non-events)

Pnew,events表示在疾病组新模型的预测阳性概率，Pold,non-events表示在非疾病组旧模型的预测阳性概率。

IDI就等于疾病组新旧模型的预测阳性概率的差值减去非疾病组新旧模型预测阳性概率的差值（因为对于非疾病组模型预测阳性的概率应该是越小越好，所以中间是减号）

结果解读：IDI越大越说明新模型比旧模型预测效果更好。若IDI＞0，则为正改善，说明新模型比旧模型的预测能力有所改善，若IDI＜0，则为负改善，新模型预测能力下降，若IDI=0，则认为新模型没有改善。

二分类资料

案例：预测肺动脉栓塞风险

library(readxl)
data <- read_excel("data.xlsx")
data<-na.omit(data)
data<-as.data.frame(data)

?创建Logistic预测模型

#建立模型公式
form.bestglm<-as.formula(group~age+BMI+ToS+CA153+CDU+transfusion+stage)
form.all<-as.formula(group~.)
#打包
library(rms)
dd=datadist(data)
options(datadist="dd")
#Logistic模型拟合
fit.glm<- lrm(formula=form.bestglm,data=data,x=TRUE,y=TRUE)  
#计算预测值
data$predvalue<-predict(fit.glm)

1. C指数

C指数计算

因为C指数在logistic回归二分类中等价于ROC，所以：

方法一：ROC计算

library(pROC)
modelROC <- roc(data$group,data$predvalue)
auc(modelROC)
ci(auc(modelROC))

提取出fit.glm中的预测值，然后利用roc（）函数进行ROC拟合。auc（）提取模型的ROC值，ci（）提取ROC的95%CI。

输出的结果可以显示AUC为0.8063，95%CI为0.7582-0.8544。所以模型的C指数为0.8063。

方法二：Hmisc包中somers2（）函数

library(Hmisc)
somers2(data$predvalue, data$group)

注意：区别于roc（）函数的顺序，roc（）函数中输入的是实际值，预测值；在somers2中输入的是预测值，后是实际值。

以上两者方法计算的C指数都是非校正的C指数

方法三：校正C指数的计算（validate（）函数）

对模型进行bootstrap，次数为1000，dxy设置为TRUE

v<-validate(fit.glm, method="boot", B=1000, dxy=TRUE)

?分别提取bootstrap后的模型中的原始Dxy和校正的Dxy，然后根据C-index=Dxy/2+0.5，计算C指数：

orig_Dxy = v[rownames(v)=="Dxy", colnames(v)=="index.orig"]
corrected_Dxy = v[rownames(v)=="Dxy", colnames(v)=="index.corrected"]
orig_C_index <- abs(orig_Dxy)/2+0.5
bias_corrected_C_index  <- abs(corrected_Dxy)/2+0.5

显示C指数结果

cbind("C指数"=orig_C_index,"校正C指数"=bias_corrected_C_index)

方法四：rcorrcens（）函数计算95%CI

c<-rcorrcens(formula=group~predvalue,data=data)
c

需要在formula中指定实际值与预测值，指定数据集data。

C指数为0.806，根据SD计算95%CI

c[1,1]-1.96*c[1,4]/2
c[1,1]+1.96*c[1,4]/2

与ROC法计算的可信区间有一定细微差别。

比较两个模型C指数

一般使用ROC法，等价于比较两个ROC曲线是否存在差异：

rm(list = ls())
library(readxl)
data <- read_excel("data.xlsx")
data<-na.omit(data)
data<-as.data.frame(data)
#建立模型公式
form.bestglm<-as.formula(group~age+BMI+ToS+CA153+CDU+transfusion+stage)
form.all<-as.formula(group~.)
#打包
library(rms)
dd=datadist(data)
options(datadist="dd")
#Logistic模型拟合
fit.glm<- lrm(formula=form.bestglm,data=data,x=TRUE,y=TRUE)  
fit2.glm<- lrm(formula=form.all,data=data,x=TRUE,y=TRUE)
#计算模型预测值
data$predvalue <- predict(fit.glm)
data$predvalue2<-predict(fit2.glm)
#ROC拟合
modelROC <- roc(data$group,data$predvalue)
modelROC2 <- roc(data$group,data$predvalue2)     
roc.test(modelROC,modelROC2 )

检验统计量Z为-1.6774，p值为0.09346，不存在统计学差异。

2. NRI

构建两个模型：

form.new<-as.formula(group~age+BMI+ToS+CA153+CDU+transfusion+stage)
form.old<-as.formula(group~ age+BMI+ToS+CDU+transfusion+stage)
mstd = glm(formula=form.old, family = binomial(), data=data, x=TRUE)
mnew = glm(formula=form.new, family = binomial(), data=data, x=TRUE)

计算分类NRI（nricens包中nribin（）函数）：

#install.packages("nricens")
library(nricens)
set.seed(123)
cg<-nribin(mdl.std =mstd,
           mdl.new = mnew,
           cut = c(0.2,0.4),
           niter = 1000,
           updown = 'category')

在计算之前需要指定种子数，种子数不同，结果会稍有差异。

nribin（）函数中mdl.std指定旧模型，mdl.new指定新模型，cut设置截断点，截断点的设置至关重要，通过不同的截断值计算出的NRI结果可能有很大差异，结合临床进行截断值的设置。本案例中，将截断值设置为0.2，0.4，截断值<0.2为低风险，截断值>0.4为高风险。niter设置bootstrap次数，updown设置“category”表示计算分类NRI。

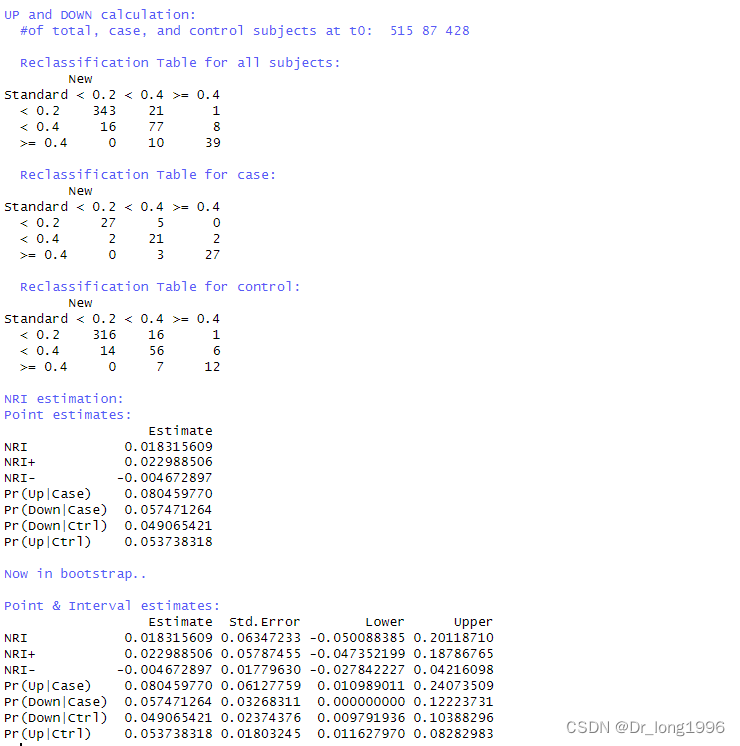
从结果可以看到总人数515，病例数87，对照组428人。

Reclassification Table for all subjects中的针对所有人的研究结果。根据设置的截断值，将病人分为了低，中，高风险。第一行new表示新模型的分类情况，standard表示旧模型的分类情况。理解即为343人在新旧模型中被认为是低风险，21在新模型中为中风险，旧模型中为低风险，1人在新模型中高风险，旧模型中低风险，以此类推。

Point estimates中表示分类NRI的点估计值。其中NRI表示所有研究对象的分类NRI的点估计值，NRI+表示病例组的分类NRI的点估计值，NRI-表示对照组中的分类NRI点估计值。

Point & Interval estimates表示NRI的置信区间。

红色表示病例组，黑色表示对照组，虚线表示截断值，

计算NRI之间的P值：

z=abs(cg$nri$Estimate/cg$nri$Std.Error)
cg$nri$pvalue<-(1-pnorm(z))*2
cg$nri

?P值均大于0.05，说明不存在统计学差异，即新旧模型相较，从分类NRI角度没有差异。

连续性NRI计算

set.seed(123)
cf<-nribin(mdl.std =mstd , 
           mdl.new = mnew, 
           cut =0, 
           niter = 1000, 
           updown = 'diff')

cut设置为0，updown设置为“diff”表示计算连续型NRI

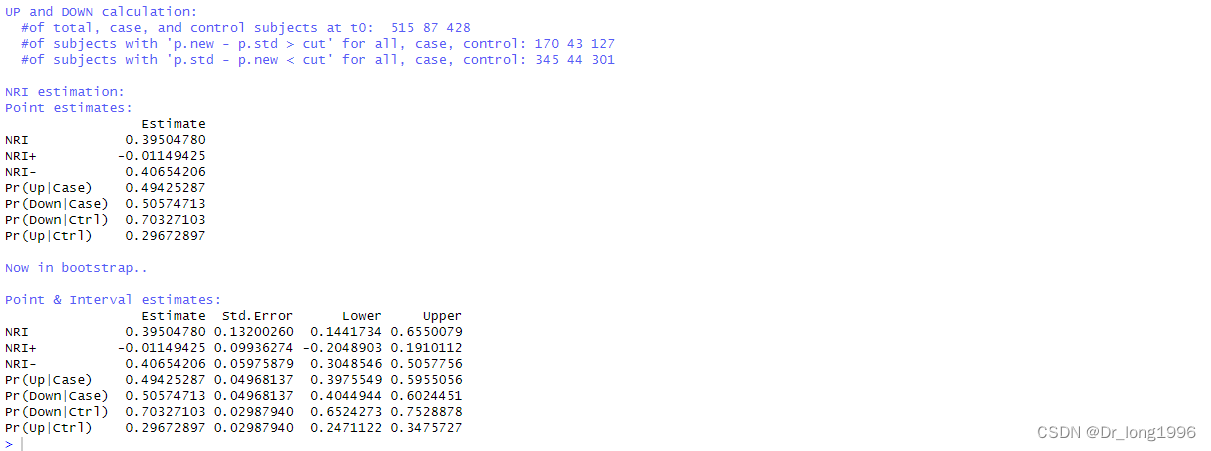
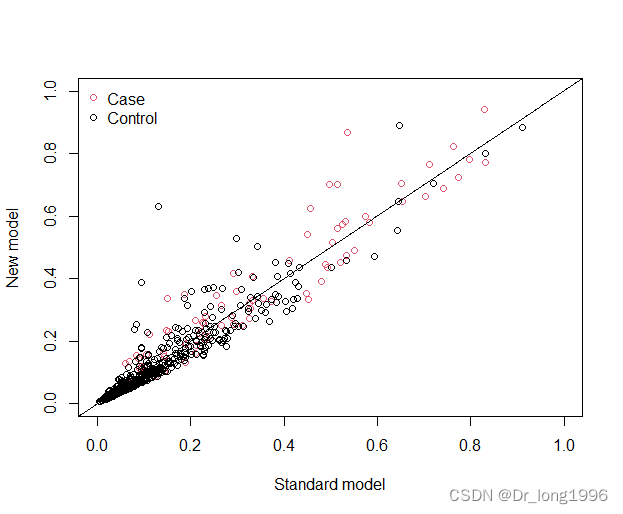
计算NRI的p值

z=abs(cf$nri$Estimate/cf$nri$Std.Error)
cf$nri$pvalue<-(1-pnorm(z))*2
cf$nri

?通过P值可以看到在连续型NRI，NRI-的P值小于0.05，存在统计学差异，即新模型相较旧模型好，对于人群提升0.395048，对于对照组提升0.4065；NRI+并无统计学意义。

3. IDI

提取出模型中的预测值fitted.values

pstd = mstd$fitted.values
pnew = mnew$fitted.values

利用PredictABEL包中的函数reclassification计算

#install.packages("PredictABEL")
library(PredictABEL)
reclassification(data=as.matrix(data),
                 cOutcome = 1,
                 predrisk1 = pstd,
                 predrisk2 = pnew,
                 cutoff = c(0,0.2,0.4,1))

需要将data处理为矩阵，cOutcome设置因变量位于矩阵的第几列；选项predrisk1指定旧模型，predrisk2指定新模型，cutoff值设置截断点。

%reclassified表示重分类百分比。

输出的最后三行分别给出了分类NRI，连续NRI，IDI的结果，以及对应的p值。从IDI角度，IDI为0.0203，95%CI为0.0041-0.0365，p值<0.05，存在统计学差异，新模型较旧模型提高了0.0203，为正改善。

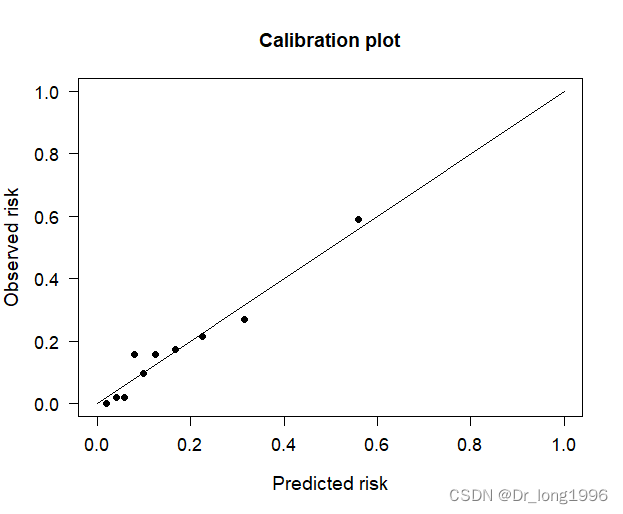
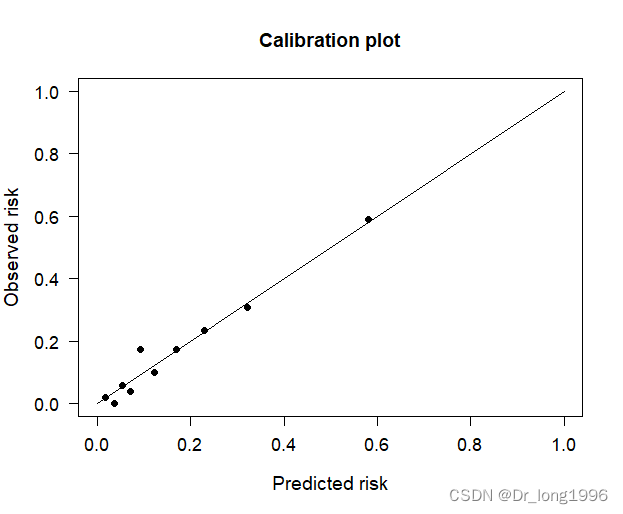
PredictABL包还可以绘制calibration曲线：

plotCalibration(data=as.matrix(data), 
                cOutcome=1, 
                predRisk=pstd, 
                groups=10, 
                rangeaxis=c(0,1))
plotCalibration(data=data, 
                cOutcome=1, 
                predRisk=pnew, 
                groups=10, 
                rangeaxis=c(0,1))

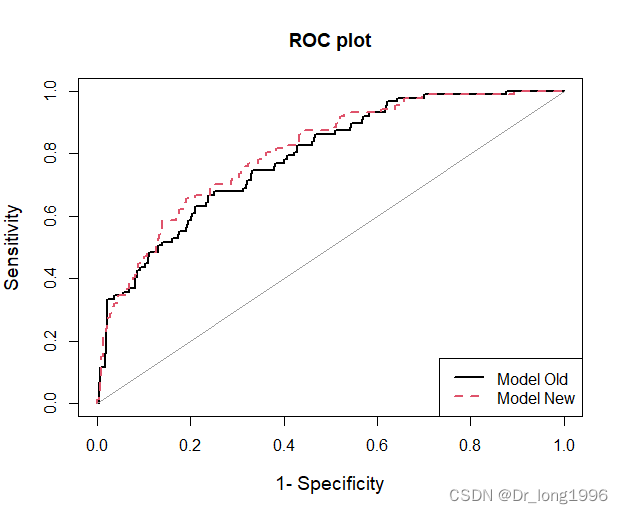
ROC曲线：

plotROC(data=data, 
        cOutcome=1, 
        predrisk=cbind(pstd,pnew),
        labels=c("Model Old","Model New"))

预测风险分布图：

plotRiskDistribution(data=data, 
                     cOutcome=1,
                     risks=pnew, 
                     interval=0.05, 
                     plottitle=maintitle, 
                     rangexaxis=c(0,1),
                     rangeyaxis=c(0,30), 
                     xlabel="Predicted risk", 
                     ylabel="Percentage", 
                     labels=c("Without outcome", "With outcome"))

生存资料

案例：原发性胆汁性肝硬化研究

1. rms包拟合的生存曲线

C指数

载入数据

load("pbc.Rdata")
pbc<-na.omit(pbc)
library(rms)
dd=datadist(pbc)
options(datadisk="dd")
fit.cox <- cph(formula=Surv(days,status) ~ascites+edema+bili+albumin+copper+prothrombin+chol,
               data=pbc,
               x=TRUE,y=TRUE,surv=TRUE)

计算C-index（pec包中的cindex（）函数）

set.seed(123)
library(pec)
c_index<-cindex(object=list(fit.cox),
                formula=Surv(days,status) ~1,
                eval.times=c(365,365*3,365*5,365*10), 
                cens.model = "marginal",
                splitMethod = "bootcv",
                B=1000)
c_index

object指定模型，formula指定为Surv（生存时间，生存结局）~1，cens.model必须为“marginal”（如果formula中的公式带有自变量，则cens.model需要为cox，结果也略有不同。）

eval.times设置需要计算的时间点的C指数；

cens.medol指定截尾数据的逆概率加权方法；

splitMethod表示才用的重抽样的方法行交叉验证；B为抽样次数。

Appcindex是指未经校正的C指数；BootCVCindex表示交叉验证的C指数。

绘制Time—C-index曲线

plot(c_index,
     xlim = c(0,4000),
     legend=FALSE)

比较两个模型的C指数

load("pbc.Rdata")
pbc<-na.omit(pbc)
library(rms)
dd=datadist(pbc)
options(datadisk="dd")
fit.cox <- cph(formula=Surv(days,status) ~ascites+edema+bili+albumin+copper+prothrombin+chol,
               data=pbc,
               x=TRUE,y=TRUE,surv=TRUE)
fit2.cox <- cph(formula=Surv(days,status) ~treatment+age+sex+ascites+hepatom+
                        spiders+edema+bili+chol+albumin+copper+alk+sgot+trig+
                        platelet+prothrombin+stage,
               data=pbc,
               x=TRUE,y=TRUE,surv=TRUE)
predvalue <- predict(fit.cox)
predvalue2 <- predict(fit2.cox)

模型比较：

#install.packages("compareC")
library(compareC)
compareC(timeX=pbc$days, statusX=pbc$status, scoreY=-predvalue, scoreZ=-predvalue2)

?模型1的C指数为0.8272，模型2的C指数为0.8485859，差值为-0.021，统计检验Z统计量为-2.414，p值为0.0158，说明两个模型之间存在统计学差异。

2. survival包拟合的生存曲线

C指数

survival包中coxph会自动计算出C指数：

library(survival)
fit2.cox<-coxph(formula=Surv(days,status) ~ascites+edema+bili+albumin+copper+prothrombin+chol,
                data=pbc)
summary(fit2.cox)
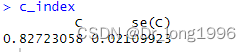
c_index<-summary(fit2.cox)$concordance
c_index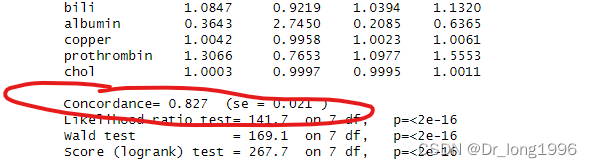

可信区间：

c_index["C"]-1.96*c_index["se(C)"]
c_index["C"]+1.96*c_index["se(C)"]

其他方法：

方法一：

BiocManager::install("survcomp")
library(survcomp)
cindex <- concordance.index(x=predvalue,
                            surv.time=pbc$days,
                            surv.event =pbc$status,
                            method = "noether")
cindex$c.index 
cindex$lower
cindex$upper

方法二：

c_index <- survConcordance(formula=Surv(days,status)~predict(fit.cox,data=pbc),
                           data = pbc)$concordance

方法三：

v <- validate(fit.cox, dxy=TRUE, B=1000)
orig_Dxy = v[rownames(v)=="Dxy", colnames(v)=="index.orig"]
corrected_Dxy = v[rownames(v)=="Dxy", colnames(v)=="index.corrected"]
orig_c_index <- abs(orig_Dxy)/2+0.5
bias_corrected_c_index  <- abs(corrected_Dxy)/2+0.5
orig_c_index;bias_corrected_c_index

NRI计算

创建新旧两个生存模型：

library(survival)
m.old = coxph(formula=Surv(days,status)~bili+albumin, 
              data=pbc, 
              x=TRUE)
m.new = coxph(formula=Surv(days,status)~bili+albumin+copper, 
              data=pbc, 
              x=TRUE)

计算分类NRI：

library(nricens)
set.seed(123)
nricens(mdl.std = m.old, 
        mdl.new = m.new, 
        t0 = 365*10,
        cut = c(0.2, 0.4),
        updown = "category",
        niter = 1000)

t0指定需要计算的时间，cut设置截断值，updown设置为分类，niter设置bootstrap的次数。

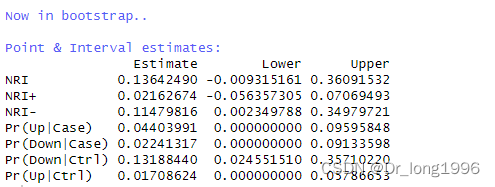
针对于全部研究对象，分类变量NRI=0.136，新模型较旧模型重新分类正确比例提高了13.6%；

针对于病例组，分类NRI=0.022，新模型较旧模型重新分类正确比例提高了2.2%；

针对于对照组，分类NRI=0.115，新模型较旧模型重新分类正确比例提高了1.1%。

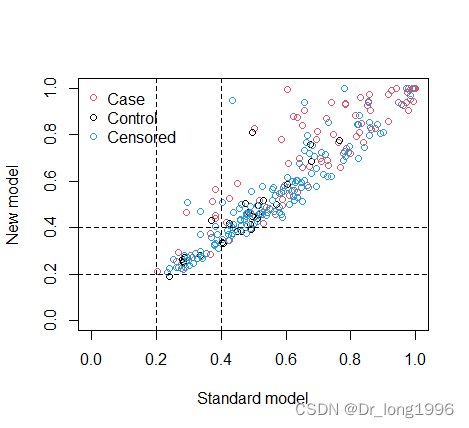
计算连续型NRI：

set.seed(123)
nricens(mdl.std = m.old,
        mdl.new = m.new, 
        t0 = 365*10, 
        cut = 0,updown = "diff", 
        niter = 1000)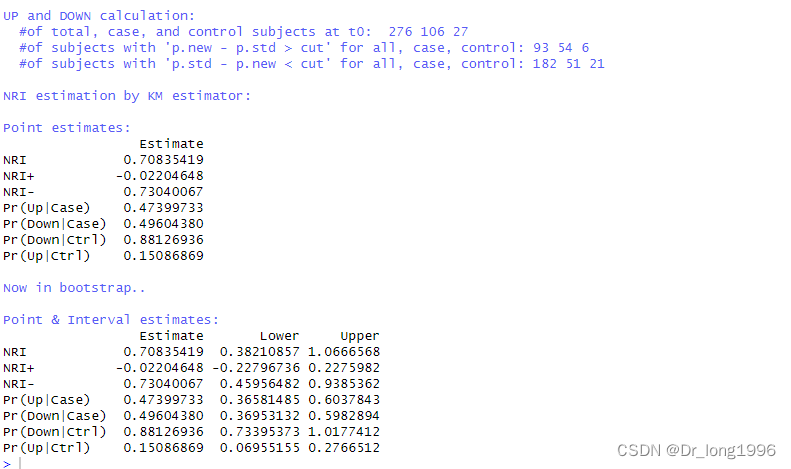

输出的结果中 of subjects with "p.new-p.std>cut" for all, case, control:93 54 6 表示在时点3650天，新模型的概率减去旧模型的概率大于截断点（0）的人数。

IDI

surv<-pbc[,c("days","status")]
x.old = pbc[,c("bili", "albumin")]
x.new = pbc[,c("bili", "albumin","copper")]

因变量赋值给surv，自变量赋值给x.old和x.new。

#install.packages("survIDINRI")
library(survIDINRI)
set.seed(123)
IDI<-IDI.INF(indata=surv,
           covs0=x.old,
           covs1=x.new,
           t0=3650,
           npert=1000) 
IDI.INF.OUT(IDI)

indata指定因变量，即是生存时间和生存结局；covs0指定旧模型的自变量，covs1指定新模型的自变量，t0指定计算时间点，npert指定bootstrap次数。

IDI.INF.OUT()函数读取出结果

M1表示IDI，IDI为0.039，其可信区间为（-0.001，0.097），p值为0.062>0.05，无统计学意义。M2表示连续NRI；M3表示中位数差异。

图形展示：

IDI.INF.GRAPH(IDI)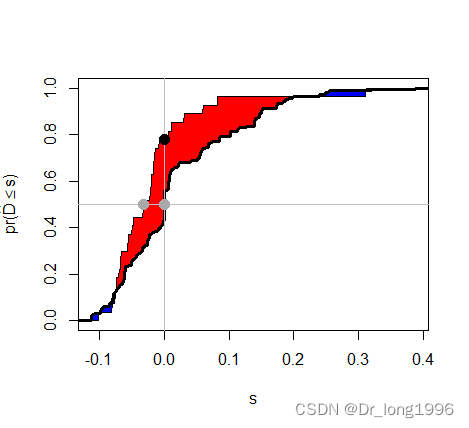

红色区域为IDI的情况，面积越大，新模型越优于原来的旧模型。

文章来源:https://blog.csdn.net/Dr_long1996/article/details/135588760
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！