【算法系列】一文彻底讲懂隐马尔可夫模型

前言

视频讲解在我女朋友的B站『你真的理解隐马尔可夫链吗？隐马尔可夫最通俗易懂的解释』

马尔科夫链或者马尔科夫性是一个非常重要的数学概念，大家在做科研或者学习过程中或多或少都听过，马尔科夫性在SLAM问题中也是非常重要的，iSAM中的因子图也是在此基础上改进而来。很多人觉得这是一个非常复杂、难懂的概念，特别是它的一些相关概念，性质，包括前向后向算法等等。

本篇文章将为大家详细讲解马尔科夫链、马尔科夫性、以及隐马尔可夫链的相关概念和问题，下一篇文章将会以一种通俗易懂的方式，为大家讲解隐马尔可夫链的前向后向算法和维特比算法。

一、贝叶斯网络

在讲解马尔科夫链之前，我们先简单了解一下贝叶斯网络，因为这是推广到马尔科夫链的基础。

贝叶斯网络是一种用图模型表示随机变量之间概率关系的工具。它基于贝叶斯定理，用有向无环图（DAG）来表示变量之间的依赖关系，并通过概率分布来描述这些依赖关系。

在一个贝叶斯网络中：

• 节点表示一个或一组随机变量
• 边表示变量之间的依赖关系

每个节点都与一个概率分布相关，该分布描述了给定其父节点值时该节点的条件概率分布。这种图形模型的结构使得我们可以通过已知信息来更新对未知变量的信念。

比如这个贝叶斯网络中，表示x2依赖于x1，x5依赖于x2和x3等等。

二、马尔科夫链

1.直观理解

马尔可夫链是一个数学概念，描述了在一系列离散事件中，从一个状态转移到另一个状态的过程。

该过程满足马尔科夫性质，即当前时刻的状态只依赖于前一时刻的状态，与更久之前的状态无关。这意味着在给定当前状态的情况下，未来的发展不受过去的影响。

马尔可夫链可以用状态空间和状态转移概率来表示。状态空间是所有可能的状态的集合，而状态转移概率描述了从一个状态到另一个状态的概率。

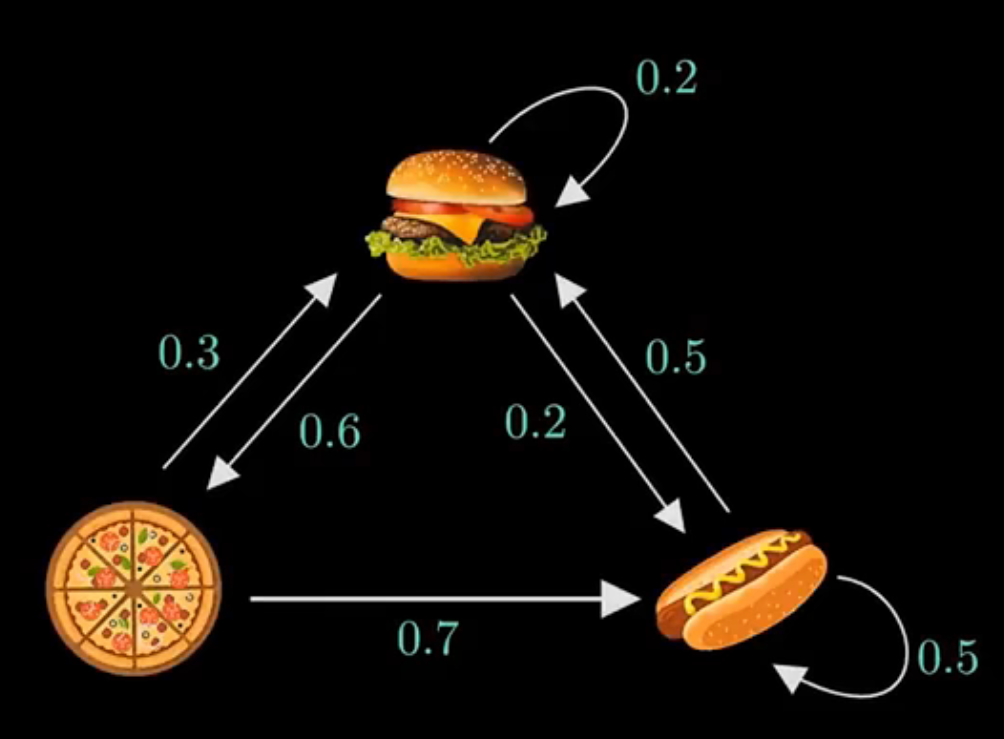
这个例子中，我们要观察快餐店供应什么食物，其中，每天供应的食物与前一天有关，比如今天供应了汉堡，那么明天则有0.2的概率还供应汉堡，0.6的概率供应披萨，0.2的概率供应热狗。

2.基本概念

（1）状态转移矩阵

状态转移矩阵是将每种状态(当天食物)转移到下一状态(明天食物)的概率表示为矩阵的形式，我们用A表示，那么上图的状态转移矩阵可以表示为：

$$A=\left[\begin{array}{ccc}0.2& 0.6& 0.2\\ 0.3& 0& 0.7\\ 0.5& 0& 0.5\end{array}\right]$$

第0行第0列表示：第0个状态(当天供应汉堡)转移到第0个状态(明天继续供应汉堡)的概率；

第2行第1列表示：第2个状态(当天供应热狗)转移到第1个状态(明天供应披萨)的概率，图中没有相应的有向边，因此值为0。

（2）稳态(初始状态概率向量)

初始状态概率向量的意义是，当我们某一天突然走进这个快餐店时，它会供应什么食物呢？或者说它供应每种食物的概率是多少呢？

我们在这个马尔科夫链上做随机漫步，漫步的次数足够多时，每一种食物供应的概率会趋于一个稳态，对这个概念有一种很直观的解释：

比如第一天供应披萨，那么对应的状态为[0,1,0]，那么我们做一次随机漫步，明天供应汉堡和热狗的概率是多少呢？我们可以用这个向量乘以转移矩阵A：

这与图中相对应，那么我们一直做随机漫步，当次数趋于无穷时，如果这个稳态真的存在，那么我们最终会达到这个稳态，得到的状态概率向量不再发生变化，这个过程可以表示为：

$$\pi A=\pi$$

有没有发现这个式子很像矩阵A的特征方程，这就说明，如果稳态真的存在，我们可以对A进行特征值分解，找到特征值1对应的特征向量，那么我们就可以求解出这个稳态。

三、隐马尔可夫链

我们上面讲的马尔科夫链，是所有状态都可以观测到，但实际上，我们可能并不能直接观测到(或准确观测到)对象的状态，只能通过一些传感器的测量间接的反应对象状态；

比如SLAM问题中，我们很难精确地观测到机器人的位置(状态)，只能得到一些传感器的观测值(坐标点)。

相应的模型隐马尔可夫链模型，隐马尔可夫链的性质是：

• 观测变量仅依赖于当前时刻的状态变量
• 当前时刻的状态仅依赖于前一时刻的状态

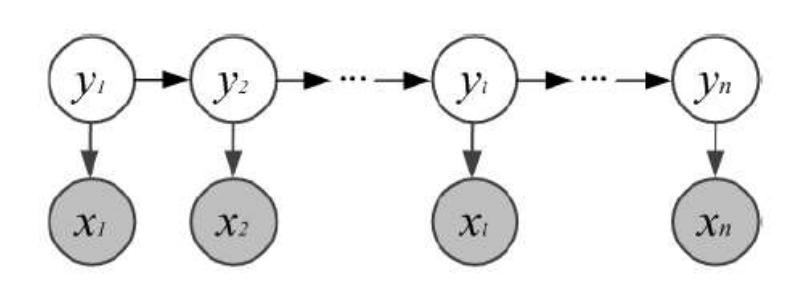
状态变量 { y 1 , y 2 , . . . , y n } \{y_1,y_2,...,y_n\} {y1?,y2?,...,yn?}，表示第t时刻的系统状态
观测变量 { x 1 , x 2 , . . . , x n } \{x_1,x_2,...,x_n\} {x1?,x2?,...,xn?}，表示第t时刻的观测值

根据上述性质，我们可以求解上图模型的联合概率：

(3)观测概率矩阵(发射矩阵)

相应的我们定义一个观测概率矩阵B，来表示当前时刻t的状态y得到当前时刻观测x的概率，同样的第i行第j列，表示当前时刻t的系统状态为i得到观测为j的概率。

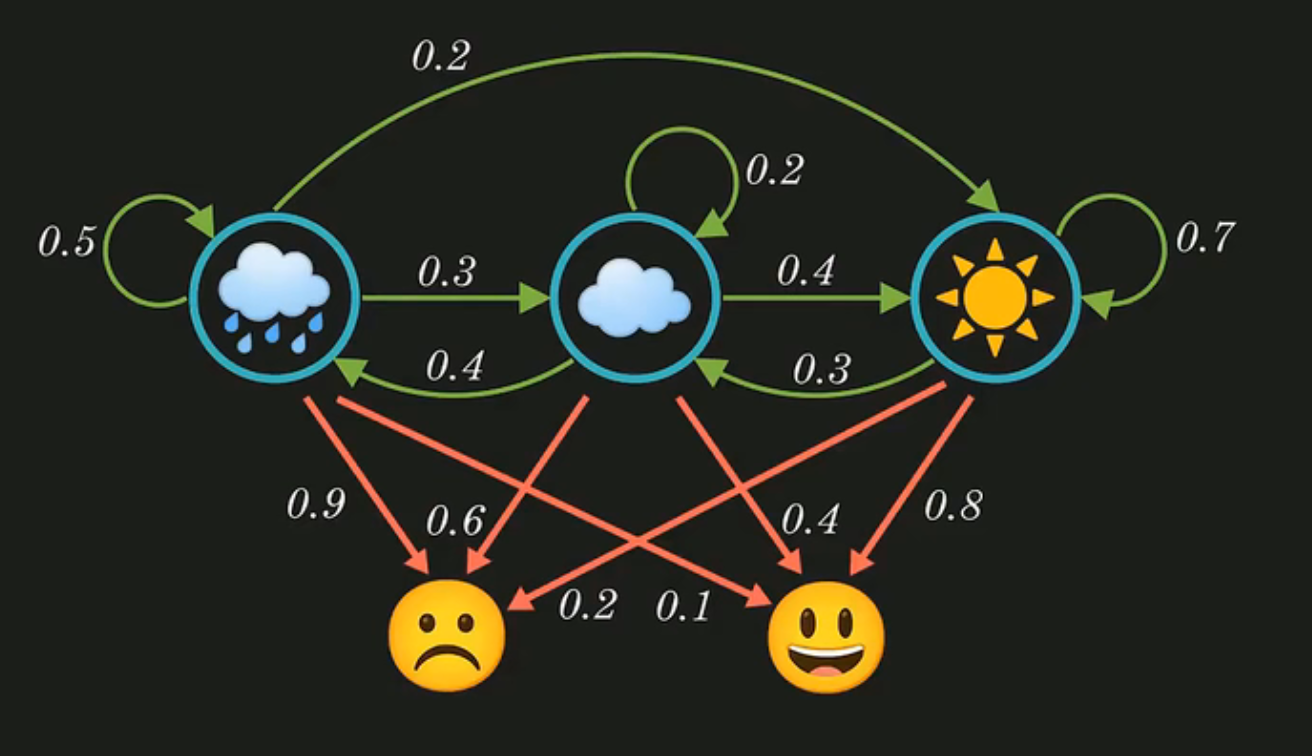
比如这个例子中，人的心情为我们能观测到的值，而当天人的心情是由当天的天气决定的，比如当天如果下雨，那么就会由0.9的概率今天不开心。我们就可以写出这个模型的状态转移矩阵A和观测概率矩阵B：

$$A=\left[\begin{array}{ccc}0.5& 0.3& 0.2\\ 0.4& 0.2& 0.4\\ 0.0& 0.3& 0.7\end{array}\right]$$
$$B=\left[\begin{array}{cc}0.9& 0.1\\ 0.6& 0.4\\ 0.2& 0.8\end{array}\right]$$

其中，观测概率矩阵B的第1行第0列表示：当天天气为阴天，得到当天人心情为不开心的概率

状态转移矩阵A、观测概率矩阵B、稳态(初始状态概率向量)π就构成了马尔科夫决策模型的三个重要元素。

四、三个基本问题

隐马尔可夫模型中有三个最基本的问题：

1. 概率计算问题：给定模型参数$\lambda =(A,B,\pi )$和观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1?,x2?,...,xn?}计算在模型参数$\lambda$下观测到x的概率$P(x|\lambda )$(评估模型和观测序列之间的匹配程度)

2. 预测问题：给定模型$\lambda =(A,B,\pi )$和观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1?,x2?,...,xn?}，求使得$P(y|x,\lambda )$最大的状态观测序列 y = { y 1 , y 2 , . . . , y n } y=\{y_1,y_2,...,y_n\} y={y1?,y2?,...,yn?}(根据观测序列推断最有可能的状态序列)

3. 学习问题：给定观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1?,x2?,...,xn?}，调整模型参数$\lambda =(A,B,\pi )$，使得该序列出现的概率$P(x|\lambda )$最大(训练模型使其更好地描述观测序列)

下一篇文章中，我们将着重讲解概率计算问题和预测问题如何求解，以及对应的前向后向算法、维特比算法。