12. 序列的特殊方法

12. 序列的特殊方法

不要通过叫声, 走路姿势等像不像鸭子来检查它是不是鸭子, 具体检查什么取决于你想使用语言的哪些行为.
(comp.lang.python, 2000年7月26日.)
                                                                            --Alex Martelli

本章将以第11章定义的二维向量类Vector2d为基础, 向前迈出一大步, 定义表示多维向量的Vector类.
这个类的行为与Python中标准的不可变扁平序列一样. 
Vector实例中的元素是浮点数, 本章结束后Vector类将支持以下功能.

? 基本的序列协议: __len__和__getitem__.
? 正确表述拥有很多元素的实例.
? 适当的切片支持, 生成新的Vector实例.
? 综合各个元素的值计算哈希值.
? 自定义的格式语言扩展.

此外, 本章还将通过__getattr__方法实现属性的动态存取, 
以取代vector2d使用的只读特性--不过, 序列类型通常不会这么做.

在大量代码之间, 本章将穿插讨论一个概念: 把协议当作正式接口.
我们将说明协议和鸭子类型之间的关系, 以及对自定义类型的实际影响.

12.1 本章新增内容

本章没有太大的变化, 12.4节在结尾处新增了一个'提示栏', 简单讨论typing.Protocol.

12.5.2节实现的__getitem__(参见示例12-6)比第1版更简洁且更强健, 这要得益于鸭子类型和operator.index.
本章后面实现的Vector和第16章也做了同样的改动.

下面开始吧!

12.2 Vector类: 用户定义的序列类型

本章将使用组合模式实现vector类, 而不使用继承.
向量的分量存储在浮点数数组中, 而且还将实现不可变扁平序列所需的方法.
不过, 在实现序列方法之前, 要先实现一个基准, 确保Vector类与前面定义的Vector2d类兼容
(没必要兼容的地方除外).

*----------------------------------------三维以上向量的应用程序---------------------------------*
谁需要1000维向量呢? 信息检索领域经常使用N维向量(N是很大的数),
因为查询的文档和文本使用向量表示, 一个单词一个维度. 这叫向量空间模型.
在这个模型中, 一个关键的相关指标是余弦相关性(表示查询的向量与表示文档的向量之间夹角的余弦).
夹角越小, 余弦值越趋近于1, 文档与查询的相关性越大.

不过, 本章定义的Vector类是为了教学而举的例子, 不会涉及很多数学原理.
我们的目的是以序列类型为背景说明Python的几个特殊方法.

如果在实际使用中需要做向量运算, 那么应该使用NumPy和SciPy.
Radim Rehürek开发的PyPI包gensim使用NumPy和SciPy实现了用于处理自然语言和检索信息的向量空间模型.
*---------------------------------------------------------------------------------------------*

12.3 Vector类第1版: 与Vector2d类兼容

Vector类的第1版要尽量与前面定义的Vector2d类兼容.
然而, 我们会故意不让Vector的构造函数与Vector2d的构造函数兼容.
为了编写Vector(3, 4)和Vector(3, 4, 5)这样的代码, 是可以让__init__方法接受任意个参数的(借助*args).
但是, 序列类型的构造函数最好接受可迭代对象为参数, 因为所有内置的序列类型都是这样做的.
示例12-1展示了Vector类的几种实例化方式.

# 示例 12-1 测试 Vector.__init__方法和 Vector.__repr__方法
>>> Vector([3.1, 4.2])
Vector([3.1,4.2])

>>> Vector((3,4,5))
Vector([3.0,4.0, 5.0])

>>> Vector(range(10))
Vector([0.0, 1.0, 2.0, 3.0, 4.0,...])

除了构造函数的新签名, 我还确保了在传入两个分量(例如Vector([3, 4]))时,
Vector2d类(例如Vector2d(3, 4))的每个测试都能通过, 而且得到相同的结果.
***-----------------------------------------------------------------------------------------***
如果vector实例的分量超过6个, 那么repr()生成的字符串就会使用...省略一部分,
如示例12-1中的最后一行所示. 包含大量元素的容器类型一定要这么做, 因为repr是用于调试的,
你肯定不想让大型对象在控制台或日志中输出几千行内容.
使用reprlib模块可以生成长度有限的表示形式, 如示例12-2所示.
在Python2.7中, reprlib模块的名称是repr.
***-----------------------------------------------------------------------------------------***

示例12-2是第1版vector类的实现代码(以示例11-2和示例11-3中的代码为基础).

# 示例12-2vector_vl.py：从vector2d_vl.py衍生而来
from array import array
import reprlib
import math


class Vector:
    typecode = 'd'
    
    def __init__(self, components):
        # self._components 是'受保护'的实例属性, 把Vector的分量保存在一个数组中。
        self._components = array(self.typecode, components)
        
    def __iter__(self):
        # 为了迭代, 使用self._components构建一个迭代器, 作为返回值. ②
        # (注1: iter()函数和__iter__方法将在第17章讨论. )
        return iter(self._components)
    
    def __repr__(self):
        # 使用reprlib.repr()函数生成self._components的有限长度表示形式
        # ( 例如 array('d', [0.0, 1.0, 2.0, 3.0, 4.0, ...])  ).
        components = reprlib.repr(self._components)  # 得到一个字符串的表现形式.
        # 把字符串插入Vector的构造函数调用之前, 去掉前面的array('d', 和后面的).
        # 意思是去掉 array('d', ) 剩下字符串格式的列表. (例如: [0.0, 1.0, 2.0, 3.0, 4.0, ...] )
        components = components[components.find('['):-1]
        return f'Vector({components})'
    
    def __str__(self):
        # 可迭代对象可以被转换为元组类型.
        return str(tuple(self))  
    
    def __bytes__(self):
        # 直接使用self._components构建bytes对象.
        return (bytes([ord(self.typecode)]) + bytes(self._components))
    
    def __eq__(self, other):
        # 判断值是否相等.
        return tuple(self) == tuple(other)
    
    def __abs__(self):
        # 从Python 3.8开始, math.hypot 接受N维坐标点.
        # 以前使用的表达式是math.sqrt( sum(x * × for x in self) ).
        return math.hypot(*self)
    
    def __bool__(self):
        # 生成对象的布尔值.
        return bool(abs(self))
    
    # 类方法
    @classmethod
    def frombytes(cls, octets):  # 将对象的bytes类型的数据转为数组.
        typecode = chr(octets[0])
        # 只需在frombytes方法的基础上改动最后一行:
        # 直接把memoryview传给构造函数, 不用像前面那样使用*拆包.
        memv = memoryview(octets[1:]).cast(typecode)
        return cls(memv)  # 指的是这一行不不用像前面那样使用*拆包.

这里使用reprlib.repr的方式需要做些说明.
这个函数用于生成大型结构或递归结构的安全表示形式, 它会限制输出字符串的长度, 用'...'表示截断的部分.
(reprlib模块中的repr()函数实现了一定的安全保障机制,
它会限制生成的字符串长度, 以防止输出的字符串过长导致系统崩溃.)
我希望Vector实例的表示形式是Vector([3.0, 4.0, 5.0]), 
而不是Vector(array('d', [3.0, 4.0, 5.0])), 因为Vector实例中的数组是实现细节. 
由于构造函数的这两种调用方式所构建的Vector对象是一样的,
因此可以选择使用更简单的句法, 即传入列表参数.

编写__repr__方法时, 
本可以使用表达式reprlib.repr(list(self._components))生成简化的components显示形式, 
然而, 这么做有点儿浪费资源, 
因为要把self._components中的每个元素复制到一个列表中, 然后使用列表的表示形式.
我没有这么做, 而是直接把self._components传给reprlib.repr函数, 然后去掉[]外面的字符,
如示例12-2中__repr__方法的第二行所示.
*--------------------------------------------------------------------------------------------*
调用repr()函数的目的是调试, 因此绝对不能抛出异常.
如果_repr_方法的实现有问题, 则必须处理, 尽量输出有用的内容, 让用户能够识别接收者(self).
*--------------------------------------------------------------------------------------------*

注意, __str__方法, __eq__方法和__bool__方法与Vector2d类中一样.
而frombytes方法也只变了一个字符(最后一行把*去掉了).
这是Vector2d可迭代的好处之一.

顺便说一下, 本可以让Vector继承Vector2d, 但是我没有那么做, 原因有二.
第一, 两个构造函数不兼容, 不适合使用继承.
这一点通过适当处理__init__方法的参数可以解决, 
不过第二个原因更重要: 我想把Vector类当作单独的示例, 以此实现序列协议.
接下来我们会先讨论'协议'这个术语, 然后再实现序列协议.

12.4 协议和鸭子类型

如第1章所述, 在Python中创建功能完善的序列类型无须使用继承, 实现符合序列协议的方法即可.
不过, 这里说的协议是什么呢?
在面向对象编程中, 协议是非正式的接口, 只在文档中定义, 不在代码中定义.
例如, Python的序列协议只需要__len__和__getitem__这两个方法.
任何类(例如Spam), 只要使用标准的签名和语义实现了这两个方法, 就能用在任何预期序列的地方.
Spam是不是哪个类的子类无关紧要, 只要提供了所需的方法即可.
示例1-1就是一例, 这里再次给出代码, 如示例12-3所示.

# 示例12-3示例1-1的代码, 为了方便参考, 再次给出
import collections
# 创建具名元组对象
Card = collections.namedtuple('Card', ['rank', 'suit'])

class FrenchDeck:
    # 卡牌大小
    ranks = [str(n) for n in range(2, 11)] + list('JQKA')
    # 卡牌花色
    suits = 'spades diamonds clubs hearts'.split()
    
	def __init__(self):
        # 生成52张卡牌
    	self._cards = [Card(rank, suit) for suit in self.suits 
                                        for rank in self.ranks]
    
    # 获取对象的卡牌数量
    def __len__(self):
		return len(self._cards)
    
    # 获取第n张卡牌
	def __getitem__(self, position):
		return self. _cards[position]
    

示例12-3中的FrenchDeck类能充分利用Python的很多功能, 因为它实现了序列协议, 即使代码中并没有声明这一点.
任何有经验的Python程序员只要看一眼就知道它是序列, 即便它是object的子类也无妨.
我们说它是序列, 因为它的行为像序列, 这才是重点.

根据本章开头引用的Alex Martelli的帖文, 人们称其为鸭子类型(duck typing).

协议是非正式的, 没有强制力, 因此如果知道类的具体使用场景, 那么通常只需要实现协议的一部分.
例如, 为了支持迭代, 只需实现__getitem__方法, 没必要提供__len__方法.
*--------------------------------------------------------------------------------------------*
实现'PEP544-Protocols: Structural subtyping (static duck typing)'之后,
Python 3.8开始支持协议类(protocol class), 即8.5.10节讲过的typing结构.
这里的'协议'与传统意义有关系, 但不完全相同. 
如果需要区分, 那么可以使用静态协议指代协议类规定的协议, 使用动态协议指代传统意义上的协议.
二者之间主要的区别是, 静态协议的实现必须提供静态类中定义的所有方法.
13.3节会进一步探讨这个话题.
*--------------------------------------------------------------------------------------------*

下面, 我们将在Vector类中实现序列协议, 该类暂不完全支持切片, 稍后再完善.

12.5 Vector类第2版：可切片的序列

如FrenchDeck类所示, 如果能委托给对象中的序列属性(例如self._components数组), 则支持序列协议特别简单.
下面只有一行代码的__len__方法和__getitem__方法是很好的开始.

class Vector:
    # 省略了很多行
	def __len__(self):
		return len(self._components)
    
	def __getitem__(self, index):
    	return self._components[index]

添加这两个方法之后, 以下操作都能执行了.

>>> v1 = Vector([3, 4, 5])
>>> len(v1)
3

>>> v1[0], v1[-1]
(3.0, 5.0)

# range得到是浮点数...
>>> v7 = Vector(range(7))

>>> v7[1:4]
array('d', [1.0, 2.0, 3.0])

可以看到, 连切片都支持了, 不过尚不完美.
如果Vector实例的切片也是Vector实例, 而不是数组, 那就更好了.
前面那个FrenchDeck类也有类似的问题: 切片得到的是列表.
对Vector来说, 如果切片生成普通的数组, 那么将会失去大量功能.

想想内置序列类型: 切片得到的都是各自类型的新实例, 而不是其他类型.

为了把Vector实例的切片也变成Vector实例, 不能简单地把切片操作委托给数组.
要分析传给__getitem__方法的参数, 做适当的处理.

下面来看Python如何把my_seq[1: 3]句法变成传给my_seq._getitem_(...)的参数.

12.5.1 切片原理

一例胜千言, 下面来看示例12-4.

# 示例12-4 观察__getitem__和切片的行为
>>> class MySeq:
...     def __getitem__(self, index):
...     	return index  # 在这个示例中, __getitem__直接返回传给它的值.
...
>>> s = MySeq()

# 单个索引, 没什么新奇的.
>>> s[1]  
1

# 1:4 表示法变成了slice(1, 4, None).
>>> s[1:4]
slice(1, 4, None)

# slice(1, 4, 2)的意思是从1开始, 到4结束, 步幅为2.
>>> s[1:4:2]
slice(1, 4, 2)

# 神奇的事发生了: 如果[]中有逗号, 那么__getitem__收到的就是元组.
>>>s[1:4:2, 9]
(slice(1, 4, 2), 9)

# 元组中甚至可以有多个slice对象.
>>> s[1:4:2, 7:9]
(slice(1, 4, 2), slice(7, 9, None))

现在, 来仔细看看slice本身, 如示例12-5所示.

# 示例12-5 查看slice类的属性

# slice 是内置的类型(首次出现于2.7.2节).
>>> slice
<class 'slice'>

# 查看slice, 我们发现它有start, stop和step这3种数据属性, 还有indices方法.
>>> dir(slice)
['__class__', '__delattr__', '__dir__', '__doc__', '__eq__',
 '__format__', '__ge__', '__getattribute__', '__gt__',
 '__hash__', '__init__', '__le__', '__lt__', '__ne__', 
 '__new__', '__reduce__', '__reduce_ex__', '__repr__', 
 '__setattr__', '__sizeof__', '__str__', '__subclasshook__', 
 'indices', 'start', 'step', 'stop']

在示例12-5中, 调用dir(slice)得到的结果中有个indices属性, 这是一个方法, 作用很大, 但是鲜为人知.
help(slice.indices)给出的信息如下.

S.indices(len) -> (start, stop, stride)
  给定长度为len的序列, 计算S表示的扩展切片的起始(start)索引和结尾(stop)索引, 以及步幅(stride).
  超出边界的索引会被截掉, 就像常规切片一样.
  
换句话说, indices方法开放了内置序列实现的棘手逻辑, 
可以优雅地处理缺失索引和负数索引, 以及长度超过目标序列的切片.
这个方法会'整顿'元组, 把start, stop和stride都变成非负数, 而且都落在指定长度序列的边界内.

下面举几个例子. 假设有一个长度为5的序列, 例如'ABCDE'.

# 'ABCDE'[:10:2]等同于'ABCDE'[0:5:2].
>>> slice(None, 10, 2).indices(5)  
(0, 5, 2)

# 'ABCDE'[-3:]等同于'ABCDE'[2:5:1].
>>> slice(-3, None, None).indices(5) 
(2, 5, 1)

在Vector类中无须使用slice.indices()方法, 因为收到切片参数时, 我们委托_components数组处理.
因此, 如果没有底层序列类型作为依靠, 那么使用这个方法能节省大量时间.
现在知道如何处理切片了, 下面来看Vector.__getitem__方法改进后的实现.

12.5.2 能处理切片的__getitem__方法

示例12-6 列出了让Vector表现为序列所需的两个方法：
__len__和__getitem__(后者现在能正确处理切片了).

# 示例12-6 vector_v2.py 的部分代码: 为vector_v1.py中的Vector类(参见示例12-2)
# 添加len_方法和getitem_方法

    def __len__(self):
        return len(self._components)

    def __getitem__(self, key):
        # 如果key参数的值是一个slice对象......
        if isinstance(key, siice): 
            # ......就获取实例的类(Vector), 然后......
            cls = type(self)
            # ......调用类的构造函数, 使用_components数组的切片构建一个新Vector实例.
            return cls(self._components[key])
        
        # 如果从key中得到的是单个索引......
        index = operator.index(key) 
        # ......就返回_components中相应的元素.
        return self._components[index] 
    

operator.index()函数背后调用特殊方法__index__.
这个函数和特殊方法在Travis Oliphant提议的
'PEP 357-Allowing Any Object to be Used for Slicing'中定义,
目的是支持NumPy中众多的整数类型作为索引和切片参数.
operator.index()和int()之间的主要区别是, 前者只有这一个用途.
例如, int(3.14)返回3, 而operator.index(3.14)抛出TypeError, 因为float值不可能是索引.
(在这里的作用相当于把key转为整型使用.)

大量使用isinstance可能表明面向对象设计得不好, 不过在__getitem__方法中使用它处理切片是合理的.
本书第1版还使用isinstance测试了key, 判断它是不是整数.
有了operator.index就不用再测试了.
如果从key中得不到索引, 那么operator.index就会抛出TypeError, 而且报错消息非常详细,
可以参见示例12-7末尾的错误消息.

把示例12-6中的代码添加到vector类中之后, 切片行为就正确了, 如示例12-7所示.

# 示例12-7 测试示例12-6中改进的Vector.__getitem__方法
>>> v7 = Vector(range(7))

# 单个整数索引只获取一个分量, 值为浮点数.
>>> v7[-1] 
6.0

# 切片索引创建一个新Vector实例.
>>> v7[1:4]
Vector([1.0, 2.0, 3.0])

# 长度为1的切片也创建一个Vector实例.
>>> v7[-1:1]
Vector([6.0])

# vector 不支持多维索引, 因此索引元组或多个切片会抛出错误.
>>> v7[1,2]  # 注意这里是逗号.
Traceback (most recent call last):
  ...
TypeError: 'tuple' object cannot be interpreted as an integer

# 省略代码, 测试足以.
from array import array
import reprlib
import operator


class Vector:
    typecode = 'd'

    def __init__(self, components):
        self._components = array(self.typecode, components)

    def __iter__(self):
        return iter(self._components)

    def __repr__(self):
        components = reprlib.repr(self._components)

        components = components[components.find('['):-1]
        return f'Vector({components})'

    def __len__(self):
        return len(self._components)

    def __getitem__(self, key):
        if isinstance(key, slice):.
            cls = type(self)
            return cls(self._components[key])

        index = operator.index(key)
        return self._components[index]


v7 = Vector(range(7))

print(v7[-1])  # 6.0

print(v7[1:4])  # Vector([1.0, 2.0, 3.0])

print(v7[-1:])  # Vector([6.0])

# vector 不支持多维索引, 因此索引元组或多个切片会抛出错误.
print(v7[1, 2])

12.6Vector类第3版: 动态存取属性

Vector2d变成Vector之后, 就无法通过名称访问向量的分量(例如v.x和v.y)了.
现在, 我们处理的向量可能有大量分量. 不过, 如果能通过单个字母访问前几个分量的话会比较方便.
例如, 用x, y和z代替v[0], v[1]和v[2].
我们想额外提供以下句法, 用于读取向量的前4个分量.

>>> v = Vector(range(10))

>>> v.x
0.0

>>> v.y, v.z,  v.t
(1.0, 2.0, 3.0)

在Vector2d中, 使用@property装饰器把x和y标记为只读特性(参见示例11-7).
可以在Vector中编写4个特性, 但这样太麻烦.

特殊方法__getattr__提供了更好的方式. 属性查找失败后, 解释器会调用__getattr__方法.
简单来说, 对于my_obj.x表达式, Python会检查my_obj实例有没有名为×的属性.
如果没有, 就到类(my_obj.__class__)中查找; 如果还没有, 就沿着继承图继续向上查找;
②如果依旧找不到, 则调用my_obj所属的类中定义的__getattr__方法,
传入self和属性名称的字符串形式(例如'x').
(注2) 属性查找机制比这复杂得多, 具体细节在第五部分讲解. 目前知道这种简单的机制即可.)

示例12-8中列出的是为Vector类定义的__getattr__方法.
这个方法的作用很简单, 它会检查所查找的属性是不是x y z t中的某个字母, 如果是, 就返回对应的向量的分量.

# 示例12-8 vector_v3.py 的部分代码: 向Vector类中添加__getattr__方法
	
    # 设定__match_args_, 让__getattr__实现的动态属性支持位置模式匹配. ③
    __match_args__ = ('x', 'y', 'z', 't')
    def __getattr__(self, name):
         # 获取Vector类, 供后面使用.
		cls = type(self)
        
		try:
             # 尝试获取 name在__match_args__中的位置.
			pos = cls.__match_args__.index(name)
        # 如果未找到name, 那么.index(name)就会抛出ValueError. 此时, 把pos设为-1.
        # (我也想在这里使用str.find之类的方法, 可惜tuple没有实现这样的方法.)
        except ValueError:
			pos = -1
         
        # 如果pos落在分量长度范围内, 就返回对应的分量.
		if 0 <= pos < len(self._components):
			return self._components[pos]
        
        # 如果执行到这里, 就抛出AttributeError，输出一个标准消息。
        msg = f'{cls. _name_!r} object has no attribute [name!r]'
        raise AttributeError(msg)
		

(注3: 尽管Python3.10才出现为模式匹配提供支持的__match_args__, 但是在旧版中设定这个属性也没有什么害.
本书第1版把这个属性命名为shortcut_names. 第2版中使用的新名称有两个职责: 
一是在 case 子句中使用时支持位置模式,
二是存储__getattr__和__setattr__的特殊逻辑实现的动态属性名称.)

__getattr__方法的实现不难, 但是这样实现还不够.
看看示例12-9中古怪的交互行为.

# 示例12-9 不恰当的行为: 为v.×赋值没有抛出错误, 但是前后矛盾

>>> v = Vector(range(5))

>>> v
Vector([0.0, 1.0, 2.0, 3.0, 4.0])

# 使用v.×获取第一个元素(v[0]).
>>> v.x
1.0

# 为v.×赋新值. 这个操作应该抛出异常.
>>> v.x = 10

# 读取v.×, 得到的是新值10.
>>> v.x
10

# 可是, 向量的分量没变.
>>> v
Vector([0.0, 1.0, 2.0, 3.0, 4.0])

你能解释为什么会这样吗? 也就是说, 如果向量的分量数组中没有新值, 那么为什么v.x会返回10?
如果不能立即给出解释, 那么再看看示例12-8前面对__getattr__方法的说明.
虽然原因不是很明显, 但它是理解本书后面内容的重要基础.
请你自己思考一番, 然后再继续往下读, 了解具体原因.


(对象.属性,  Python会检查实例有没有这个的属性.
如果没有, 就到类(对象.__class__)中查找; 如果还没有, 就沿着继承图继续向上查找;
如果依旧找不到, 则调用对象所属的类中定义的__getattr__方法, 中查找...
v.x = 10 为对象设置了x属性.)

示例12-9前后矛盾的行为是由getattr的运作方式导致的：
仅当对象没有指定名称的属性时, Python才会调用getattr方法, 这是一种后备机制.
可是, 像v.x=10这样赋值之后, v对象就有×属性了, 因此使用v.x获取×属性的值时不会再调用_getattr_方法,
解释器会直接返回v.x绑定的值, 即10. 
另外, __getattr__方法目前的实现没有考虑到self._components之外的实例属性, 
而是从这个属性中获取__match_args__列出的'虚拟属性'.

为了避免这种前后矛盾的现象, 需要改写Vector类中设置属性的逻辑.

回想第11章最后一个Vector2d示例, 如果为.×或.y实例属性赋值, 就会抛出AttributeError.
为了避免歧义, 在Vector类中, 当为名称是单个小写字母的属性赋值时, 我们也想抛出那个异常.
为此, 要实现__setattr__方法, 如示例12-10所示.

# 示例12-10 vector_v3.py的部分代码: 在Vector类中实现__setattr__方法

    def __setattr__(self, name, value):
        cls = type(self)
        # 特别处理名称是单个字符的属性.
        if len(name) == 1:
            # 如果name在__match_args__中, 就设置特殊的错误消息.
            if name in cls.__match_args__:  # 只读属性 {attr_name!r}
                error = 'readonly attribute {attr_name!r}'  
            # 如果name是小写字母, 就设置一个针对所有小写字母的错误消息.
            elif name.islower():  # 无法在{cls_name!r}中将属性设置为'a - z'
                error = "can't set attributes 'a' to 'z' in {cls_name!r}" 
            # 否则, 把错误消息设为空字符串.
            else:
                error = ''
            # 如果错误消息不为空, 就抛出AttributeError.
            if error:
                msg = error.format(cls_name=cls.__name__, attr_name=name)
                raise AttributeError(msg)
                
        # 默认情况: 在超类上调用__setattr__方法, 提供标准行为.
        super()._setattr_(name, value)

*---------------------------------------------------------------------------------------------*
super()函数用于动态访问超类的方法, 对Python这种支持多重继承的动态语言来说, 必须这么做.
程序员经常使用这个函数把子类方法的某些任务委托给超类中适当的方法, 如示例12-10所示.
14.4节会进一步探讨super函数.
*---------------------------------------------------------------------------------------------*

为了给AttributeError选择错误消息, 我首先查看了内置类型complex的行为, 
因为complex对象是不可变的, 而且有一对数据属性: real和imag.
如果试图修改任何一个属性, 那么complex实例就会抛出AttributeError, 
错误消息是"can't set attribute".
而如果尝试为受特性保护的只读属性赋值(像11.7节那样做), 则得到的错误消息是'readonly attribute'.
在__setitem__方法中为error字符串选词时, 我参考了这两个错误消息, 而且更为明确地指出了禁止赋值的属性.

注意, 我们没有禁止为所有属性赋值, 只是禁止为单个小写字母属性赋值, 以防与只读属性x, y, z和t混淆.

***-----------------------------------------------------------------------------------------***
我们知道, 在类中声明__slots__属性可以防止设置新实例属性.
因此, 你可能想使用这个功能, 而不像这里所做的那样实现__setattr__方法.
可是, 正如11.11.2节指出的, 不建议只为了避免创建实例属性而使用__slots__,
__slots__只应该用于节省内存, 而且仅当内存严重不足时才应该这么做.
***-----------------------------------------------------------------------------------------***

虽然这个示例不支持为Vector分量赋值, 但是有一个问题要特别注意:
大多数时候，如果实现了__getattr__方法, 那么也要定义__setattr__方法, 以防对象的行为不一致.
如果想允许修改分量, 则可以实现__setitem__方法以支持v[0] = 1.1这样的赋值, 
以及(或者)实现__setattr__方法以支持v.x = 1.1这样的赋值.
不过, 我们要保持Vector是不可变的, 因为12.7节将把它变成可哈希的.

12.7 Vector类第4版: 哈希和快速等值测试

我们要再次实现__hash__方法. 加上现有的__eq__方法, 这会把Vector实例变成可哈希的对象.

Vector2d中的__hash__方法(参见示例11-8)会计算包含self.x和self.y这两个分量的元组的哈希值.
现在要处理的分量或许有上千个, 因此构建元组消耗的资源可能太多.
鉴于此, 我们将使用^(异或)运算符依次计算各个分量的哈希值, 就像这样:v[O] ^ v[1] ^ v[2].
这正是functools.reduce函数的作用. 
虽然之前我说过reduce没有以往那么常用了, ④但是计算向量所有分量的哈希值非常适合使用这个函数.
reduce函数的整体思路如图12-1所示.

(注4: sum, any和al1涵盖了reduce的大部分用途. 详见'map, filter和reduce的现代替代品'一节的讨论.)

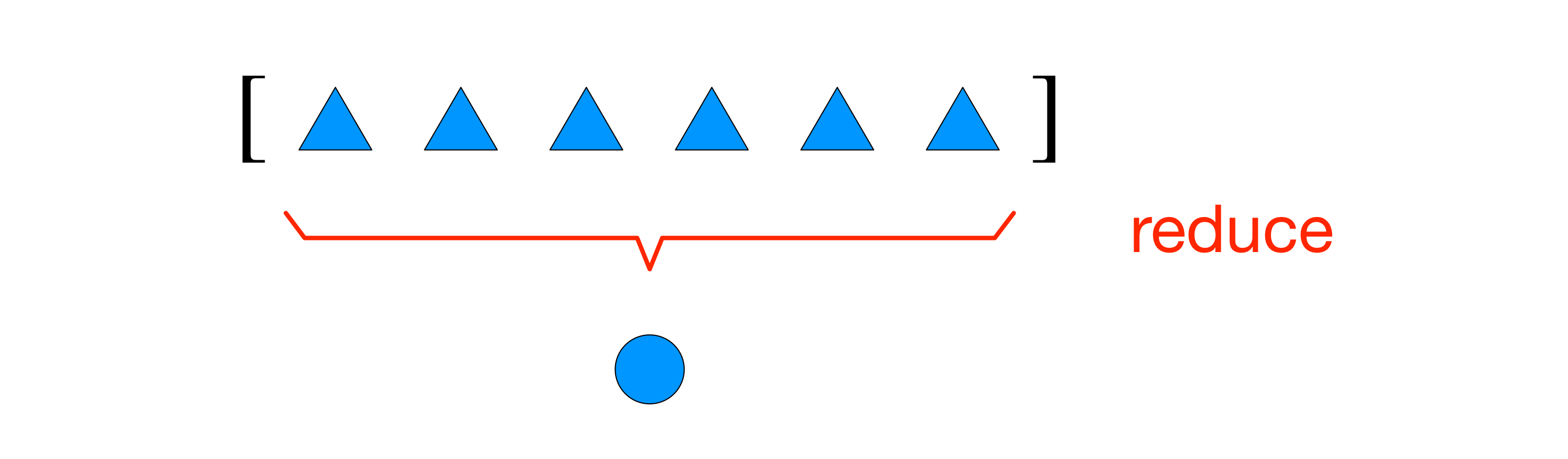
图12-1: 归约函数(reduce, sum, any和al1)把序列或有限的可迭代对象聚合成一个结果.

我们已经知道, sum()可以代替functools.reduce(), 下面说说它的原理.
reduce()的关键思想是, 把一系列值归约成单个值.
reduce()函数的第一个参数是一个接受两个参数的函数, 第二个参数是一个可迭代对象.
假如有一个接受两个参数的函数fn和一个列表lst, 调用reduce(fn, 1st)时,
fn首先会被应用到第一对元素上, 即fn(lst[0], lst[1]), 生成第一个结果r1.
然后, fn会被应用到r1和下一个元素上, 即fn(r1, lst[2]), 生成第二个结果r2.
接着, 调用fn(r2, lst[3]), 生成r3......直到最后一个元素, 返回最后得到的结果rN.

# 使用reduce函数可以计算5!(5的阶乘).
>>> 2 * 3 * 4 * 5  # 想要的结果是5! == 120
120

>>> import functools
>>> functools.reduce(lambda a, b: a * b, range(1, 6))
120

回到哈希问题上.
示例12-11展示了计算聚合异或的3种方式: 一种使用for循环, 其余两种使用reduce函数.

# 示例12-11 计算整数0-5的累计异或的3种方式

>>> n = 0

# 使用for循环和累加器变量计算聚合异或.
>>> for i in range(1, 6):
...     n ^= i
...
>>> n
1

>>> import functools
# 使用functools.reduce函数, 传入匿名函数.
>>> functools.reduce(lambda a, b: a ^ b, range(6))
1

>>> import operator
# 使用functools.reduce函数, 把lambda表达式换成operator.xor(按位异或运算的函数).
>>> functools.reduce(operator.xor, range(6)) 
1

示例12-11的3种方式中, 我最喜欢最后一种, 其次是for循环. 你呢?

7.8.1节讲过, operator模块以函数的形式提供了所有的Python中级运算符.
借此可以减少使用lambda表达式的必要.

为了使用我喜欢的方式编写Vector.__hash__方法, 需要导入functools模块和operator模块.
Vector类的相关改动如示例12-12所示.

# 示例12-12 vector_v4.py的部分代码: 
# 在vector_v3.py中的vector类的基础上导入两个模块, 并添加_hash__方法

from array import array
import reprlib
import math
# 为了使用reduce函数, 导入functools模块.
import functools
# 为了使用xor函数, 导入operator模块.
import operator


class Vector:
    typecode ='d'
    # 排版需要, 省略了很多行...
    
    # __eq__方法没有变化.
    # 这里把它列出来是为了将其和__hash__方法放在一起, 因为它们要结合在一起使用.
    def __eq__(self, other): 
    return tuple(self) == tuple(other)

    def __hash__(self):
        # 创建一个生成器表达式, 惰性计算各个分量的哈希值.
        hashes = (hash(x) for x in self._components)
        # 把hashes提供给reduce函数, 使用xor函数计算聚合的哈希值,
        # 第三个参数(0)是初始值(参见下面的'警告栏').
        return functools.reduce(operator.xor, hashes, 0) 
    
    # 又省略了很多行...
    

***-----------------------------------------------------------------------------------------***
使用reduce函数时最好提供第三个参数reduce(function, iterable, initializer),
避免如下异常: TypeError: reduce() of empty sequence with no initial value
(这个错误消息很棒, 不仅说明了问题，还提供了解决方法).
如果序列为空, 那么返回值就是initializer; 否则, 在归约循环中, 以initializer作为第一个参数.
因此, initializer应该是所执行操作的幺元值(identity value).
例如, 对+, |和^来说, initializer应该是0;
而对*和&来说, initializer应该是1.
***-----------------------------------------------------------------------------------------***

示例12-12实现的__hash__方法是一种完美的映射归约(map-reduce)计算, 如图12-2所示.

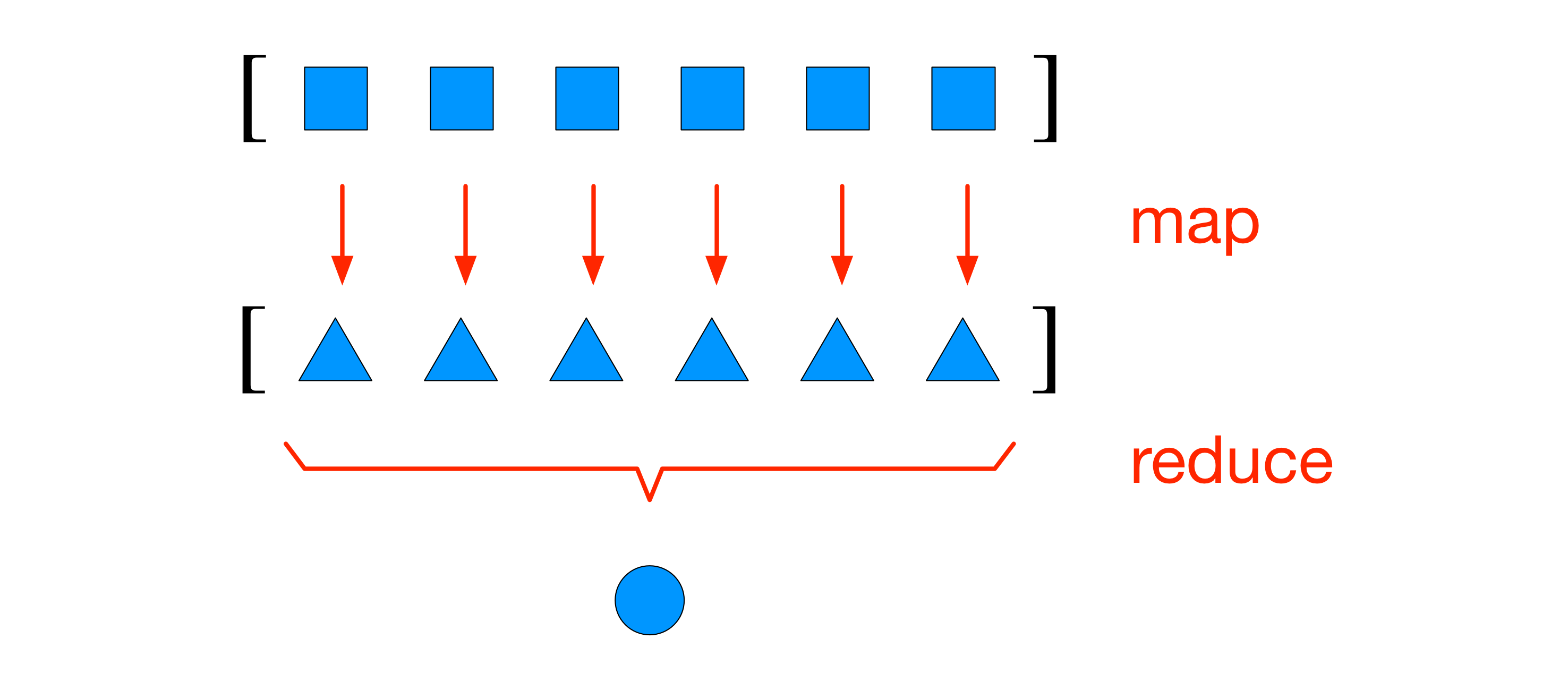
图12-2: 映射归约: 把函数应用到各个元素上, 生成一个新序列(映射), 然后计算聚合值(归约).

映射过程会计算各个分量的哈希值, 归约过程则使用xor运算符聚合所有的哈希值.
把'生成器表达式'替换成map函数, 映射过程更明显.

    def __hash__(self):
    	hashes = map(hash, self._components)
    	return functools.reduce(operator.xor, hashes)
    

*---------------------------------------------------------------------------------------------*
在Python 2中使用map函数效率低一些, 因为map函数要使用结果构建一个新列表.
但是在Python 3中, map函数是惰性的, 它会创建一个生成器, 按需产出结果,
因此能节省内存--这与示例12-8中使用生成器表达式定义__hash__方法的原理一样.
*---------------------------------------------------------------------------------------------*

既然讲到了归约函数, 那就把前面草草实现的__eq__方法修改一下, 
减少处理时间和内存用量--至少对大型向量来说如此.
示例11-2实现的__eq__方法非常简洁.

    def __eq__(self, other):
    	return tuple(self) == tuple(other)
    

Vector2d和vector都可以这样做, 甚至还会认为Vector([1, 2])和(1, 2)相等.
这或许是个问题, 不过可以暂且忽略.
⑤可是, 当Vector实例有上千个分量时, 效率十分低下.
(注5: 16.2节将认真对待Vector([1, 2]) == (1, 2）问题.)
上述实现方式要完整复制两个运算对象, 构建两个元组, 而这么做只是为了使用tuple类型的__eq_方法.
对于vector2d(只有两个分量), 这是个捷径, 但是对维数很多的向量来说情况就不同了.
示例12-13中比较两个Vector实例或者与一个可迭代对象比较的方式更好.

# 示例12-13 为了提高比较效率, Vector.__eq__方法在for循环中使用zip函数

    def __eq__(self, other):
        # 如果两个对象的长度不一样, 那么它们就不相等.
        if len(self) != len(other):
            return False
        """
        zip函数生成一个由元组构成的生成器, 元组中的元素来自参数传入的各个可迭代对象.
        如果不熟悉zip函数, 请阅读后面的'出色的zip函数'附注栏.
        前面比较长度的测试是有必要的, 因为一旦有一个输入对象耗尽, 
        zip函数就会立即停止生成值, 而且不发出警告.
        只要有两个分量不同, 就返回False, 退出.
        """
        for a, b in zip(self, other):
            if a!= b:
                return False
        # 否则, 两个对象是相等的.
        return True

*---------------------------------------------------------------------------------------------*
zip函数的名称取自拉链, 因为此物品把两边的链牙咬合在一起, 这形象地说明了zip(left, right)的作用.
zip函数与文件压缩没有关系.
*---------------------------------------------------------------------------------------------*

示例12-13的效率很好, 不过用于计算聚合值的整个for循环可以替换成一行all函数调用.
如果所有对应分量的比较结果都是True, 那么结果就是True.
只要有一次比较的结果是False, all函数就会返回False.
使用all函数实现__eq__方法的方式如示例12-14所示.

# 示例12-14 使用zip 函数和all函数实现Vector.__eq__方法, 逻辑与示例12-13一样

        def __eq__(self, other):
            return len(self) == len(other) and all(a == b for a, b in zip(self, other))
        

注意, 需要先检查两个运算对象的长度是否相同, 因为zip函数会在最短的那个运算对象耗尽时停止.

我们选择在vector_v4.py中采用示例12-14中实现的_eq_方法.

*-----------------------------------------出色的zip函数----------------------------------------*
使用for循环迭代元素无须处理索引变量, 还能避免很多bug, 
但是需要一些特殊的实用函数协助, 其中一个是内置函数zip.
使用zip函数能轻松地并行迭代两个或更多个可迭代对象, 返回的元组可以拆包成变量,
分别对应各个输入对象中的一个元素. 如示例12-15所示.

# 示例12-15 内置函数zip的使用示例

# zip函数返回一个生成器, 按需生成元组。
>>> zip(range(3), 'ABC')
<zip object at 0x10063ae48>

# 为了输出, 构建一个列表. 通常, 我们会迭代生成器.
>>> list(zip(range(3), 'ABC'))
[(0, 'A'), (1, 'B'), (2, 'C')]

# 当一个可迭代对象耗尽后, zip不发出警告就停止.
>>> list(zip(range(3), 'ABC', [0.0, 1.1, 2.2, 3.3])) 
[(0, 'A', 0.0),(1, 'B', 1.1), (2, 'C', 2.2)]

# itertools.zip_longest 函数的行为有所不同, 它使用可选的fillvalue(默认值为None)来填充缺失的值, 
# 因此可以继续生成元组, 直到最后一个可迭代对象耗尽.
>>> from itertools import zip_longest 
>>> list(zip_longest(range(3), 'ABC', [0.0, 1.1, 2.2, 3.3], fillvalue=-1))
[(0, 'A', 0.0),(1, 'B', 1.1),(2, 'c', 2.2), (-1, -1, 3.3)]

***-----------------------------------------------------------------------------------------***
Python 3.10为zip()增加的选项
本书第1版说过, zip毫无征兆地在最短的可迭代对象耗尽后停止, 这很是奇怪, 优秀的API不应这么做.
默不作声忽略输入的一部分可能导致难以察觉的bug. 
如果各个可迭代对象的长度不同, 那么zip就应该抛出valueError,
就像把可迭代对象拆包到长度不同的变量元组时那样, 与Python的快速失败策略保持一致.
'PEP 618—Add Optional Length-Checking To zip'
提议为zip函数增加一个可选的参数strict, 以表现这种行为. PEP618在Python 3.10中已经实现.
***-----------------------------------------------------------------------------------------***

# zip函数还可以转置以嵌套的可迭代对象表示的矩阵.
>>> a =[(1, 2, 3),
...     (4, 5, 6)]

>>> list(zip(*a))
[(1, 4), (2, 5),(3, 6)]

>>>b =[(1, 2), (3, 4), (5, 6)]
>>> list(zip(*b))
[(1, 3, 5), (2, 4, 6)]

如果想掌握zip函数, 那么请花点儿时间研究一下这几个示例.
为了避免在for循环中直接处理索引变量, 还经常使用内置生成器函数enumerate.
如果不熟悉这个函数, 那么一定要阅读'Built-in functions'文档.
内置函数zip和enumerate, 以及标准库中其他几个生成器函数将在17.9节讨论.
*---------------------------------------------------------------------------------------------*

本章最后要像Vector2d类那样, 为Vector类实现__format__方法.

12.8 Vector类第5版：格式化

Vector类的__format__方法类似于Vector2d类的方法, 但是不使用极坐标, 
而使用球面坐标(也叫'超球面'坐标), ⑥因为Vector类支持n个维度, 而超过四维后, 球体变成了'超球体'.
因此, 我们将把自定义的格式后缀由'p'改成'h'.
(注6: Wolfram Mathworld网站中有一篇介绍超球体的文章.)

*---------------------------------------------------------------------------------------------*
11.6节说过, 扩展格式规范微语言时. 最好避免重用支持内置类型的格式代码.
这里对微语言的扩展还会用到浮点数的格式代码'eEfFgGn%', 而且会保特原意, 因此绝对要避免重用代码.
整数使用的格式代码是'bcdoxXn', 字符串使用的是's'.
在Vector2d类中, 我选择使用'p'表示极坐标. 使用'h'表示超球面坐标是不错的选择. 
*---------------------------------------------------------------------------------------------*

例如, 对四维空间(len(v)==4)中的Vector对象来说, 'h'代码得到的结果如下:
<r, Φ1, Φ2, Φ3>, 其中r是模(abs(v)), 余下3个数是角坐标Φ1, Φ2和Φ3.

下面几个示例摘自vector_v5.py中的doctest(参见示例12-16), 演示了四维球面坐标格式.

>>> format(Vector([-1, -1, -1 , -1]), 'h')
'<2.0, 2.0943951023931957, 2.186276035465284, 3.9269908169872414>

>>> format(Vector([2, 2, 2, 2]), '.3eh')
'<4.000e+00, 1.047e+00, 9.553e-01, 7.854e-01>'

>>> format(Vector([0, 1, 0, 0]), '0.5fh')
'<1.00000, 1.57080, 0.00000, 0.00000>'

在小幅改动__format__方法之前, 要定义两个辅助方法: 一个是angle(n), 用于计算某个角坐标(例如Φ1);
另一个是angles(), 用于返回由所有角坐标构成的可迭代对象.
本书不会讲解其中涉及的数学原理, 如果你对此感到好奇, 可以查看维基百科中的'n维球体'词条,
我就是使用那里的几个公式把Vector分量数组内的笛卡儿坐标转换成球面坐标的.

示例12-16是vector_v5.py脚本的完整代码, 包含自12.3节以来实现的所有代码和本节实现的自定义格式.

# 示例12-16 vector_v5.py: Vector类最终版的doctest和全部代码,
# 带标号那几行是为了支持__format__方法而添加的代码

"""
一个多维``Vector``类, 第5版

``Vector``实例使用数值可迭代对象构建::

    >>> Vector([3.1, 4.2])
    Vector([3.1, 4.2])
    >>> Vector((3, 4, 5))
    Vector([3.0, 4.0, 5.0])
    >>> Vector(range(10))
    Vector([0.0, 1.0, 2.0, 3.0, 4.0, ...])


测试二维向量(结果与 ``vector2d_v1.py``一样)::

    >>> v1 = Vector([3, 4])
    >>> x, y = v1
    >>> x, y
    (3.0, 4.0)
    >>> v1
    Vector([3.0, 4.0])
    >>> v1_clone = eval(repr(v1))
    >>> v1 == v1_clone
    True
    >>> print(v1)
    (3.0, 4.0)
    >>> octets = bytes(v1)
    >>> octets
    b'd\\x00\\x00\\x00\\x00\\x00\\x00\\x08@\\x00\\x00\\x00\\x00\\x00\\x00\\x10@'
    >>> abs(v1)
    5.0
    >>> bool(v1), bool(Vector([0, 0]))
    (True, False)


测试类方法 ``.frombytes()``::

    >>> v1_clone = Vector.frombytes(bytes(v1))
    >>> v1_clone
    Vector([3.0, 4.0])
    >>> v1 == v1_clone
    True


测试三位向量::

    >>> v1 = Vector([3, 4, 5])
    >>> x, y, z = v1
    >>> x, y, z
    (3.0, 4.0, 5.0)
    >>> v1
    Vector([3.0, 4.0, 5.0])
    >>> v1_clone = eval(repr(v1))
    >>> v1 == v1_clone
    True
    >>> print(v1)
    (3.0, 4.0, 5.0)
    >>> abs(v1)  # doctest:+ELLIPSIS
    7.071067811...
    >>> bool(v1), bool(Vector([0, 0, 0]))
    (True, False)


测试多维向量::

    >>> v7 = Vector(range(7))
    >>> v7
    Vector([0.0, 1.0, 2.0, 3.0, 4.0, ...])
    >>> abs(v7)  # doctest:+ELLIPSIS
    9.53939201...


测试 ``.__bytes__`` 和 ``.frombytes()`` 方法::

    >>> v1 = Vector([3, 4, 5])
    >>> v1_clone = Vector.frombytes(bytes(v1))
    >>> v1_clone
    Vector([3.0, 4.0, 5.0])
    >>> v1 == v1_clone
    True


测试序列行为::

    >>> v1 = Vector([3, 4, 5])
    >>> len(v1)
    3
    >>> v1[0], v1[len(v1)-1], v1[-1]
    (3.0, 5.0, 5.0)


测试切片::

    >>> v7 = Vector(range(7))
    >>> v7[-1]
    6.0
    >>> v7[1:4]
    Vector([1.0, 2.0, 3.0])
    >>> v7[-1:]
    Vector([6.0])
    >>> v7[1,2]
    Traceback (most recent call last):
      ...
    TypeError: 'tuple' object cannot be interpreted as an integer


测试动态属性访问::

    >>> v7 = Vector(range(10))
    >>> v7.x
    0.0
    >>> v7.y, v7.z, v7.t
    (1.0, 2.0, 3.0)

动态属性查找失败情况::

    >>> v7.k
    Traceback (most recent call last):
      ...
    AttributeError: 'Vector' object has no attribute 'k'
    >>> v3 = Vector(range(3))
    >>> v3.t
    Traceback (most recent call last):
      ...
    AttributeError: 'Vector' object has no attribute 't'
    >>> v3.spam
    Traceback (most recent call last):
      ...
    AttributeError: 'Vector' object has no attribute 'spam'


测试哈希::

    >>> v1 = Vector([3, 4])
    >>> v2 = Vector([3.1, 4.2])
    >>> v3 = Vector([3, 4, 5])
    >>> v6 = Vector(range(6))
    >>> hash(v1), hash(v3), hash(v6)
    (7, 2, 1)


大多数非整数的哈希码在32位和64位CPython中不一样::

    >>> import sys
    >>> hash(v2) == (384307168202284039 if sys.maxsize > 2**32 else 357915986)
    True


测试使用``format()``格式化二维笛卡儿坐标::

    >>> v1 = Vector([3, 4])
    >>> format(v1)
    '(3.0, 4.0)'
    >>> format(v1, '.2f')
    '(3.00, 4.00)'
    >>> format(v1, '.3e')
    '(3.000e+00, 4.000e+00)'


测试使用 ``format()`` 格式化三维和七维笛卡尔坐标::

    >>> v3 = Vector([3, 4, 5])
    >>> format(v3)
    '(3.0, 4.0, 5.0)'
    >>> format(Vector(range(7)))
    '(0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0)'


测试使用 ``format()`` 格式化二维和四维球面坐标::

    >>> format(Vector([1, 1]), 'h')  # doctest:+ELLIPSIS
    '<1.414213..., 0.785398...>'
    >>> format(Vector([1, 1]), '.3eh')
    '<1.414e+00, 7.854e-01>'
    >>> format(Vector([1, 1]), '0.5fh')
    '<1.41421, 0.78540>'
    >>> format(Vector([1, 1, 1]), 'h')  # doctest:+ELLIPSIS
    '<1.73205..., 0.95531..., 0.78539...>'
    >>> format(Vector([2, 2, 2]), '.3eh')
    '<3.464e+00, 9.553e-01, 7.854e-01>'
    >>> format(Vector([0, 0, 0]), '0.5fh')
    '<0.00000, 0.00000, 0.00000>'
    >>> format(Vector([-1, -1, -1, -1]), 'h')  # doctest:+ELLIPSIS
    '<2.0, 2.09439..., 2.18627..., 3.92699...>'
    >>> format(Vector([2, 2, 2, 2]), '.3eh')
    '<4.000e+00, 1.047e+00, 9.553e-01, 7.854e-01>'
    >>> format(Vector([0, 1, 0, 0]), '0.5fh')
    '<1.00000, 1.57080, 0.00000, 0.00000>'
"""

from array import array
import reprlib
import math
import functools
import operator
# 为了再__format__方法中使用chain函数, 导入itertools模式
import itertools


class Vector:
    typecode = 'd'

    def __init__(self, components):
        self._components = array(self.typecode, components)

    def __iter__(self):
        return iter(self._components)

    def __repr__(self):
        components = reprlib.repr(self._components)
        components = components[components.find('['):-1]
        return f'Vector({components})'

    def __str__(self):
        return str(tuple(self))

    def __bytes__(self):
        return (bytes([ord(self.typecode)]) +
                bytes(self._components))

    def __eq__(self, other):
        return (len(self) == len(other) and
                all(a == b for a, b in zip(self, other)))

    def __hash__(self):
        hashes = (hash(x) for x in self)
        return functools.reduce(operator.xor, hashes, 0)

    def __abs__(self):
        return math.hypot(*self)

    def __bool__(self):
        return bool(abs(self))

    def __len__(self):
        return len(self._components)

    def __getitem__(self, key):
        if isinstance(key, slice):
            cls = type(self)
            return cls(self._components[key])
        index = operator.index(key)
        return self._components[index]

    __match_args__ = ('x', 'y', 'z', 't')

    def __getattr__(self, name):
        cls = type(self)
        try:
            pos = cls.__match_args__.index(name)
        except ValueError:
            pos = -1
        if 0 <= pos < len(self._components):
            return self._components[pos]
        msg = f'{cls.__name__!r} object has no attribute {name!r}'
        raise AttributeError(msg)
    
    # 使用'n维球体'词条中的公式计算某个角坐标
    def angle(self, n):  
        r = math.hypot(*self[n:])
        a = math.atan2(r, self[n-1])
        if (n == len(self) - 1) and (self[-1] < 0):
            return math.pi * 2 - a
        else:
            return a
    
    # 创建生成器表达式, 按需计算所有角坐标.
    def angles(self):  
        return (self.angle(n) for n in range(1, len(self)))

    def __format__(self, fmt_spec=''):
        if fmt_spec.endswith('h'):  # 超球坐标; 理想坐标
            fmt_spec = fmt_spec[:-1]
            # 用itertools.chain函数生成生成器表达式, 无缝迭代向量的模和各个角坐标.
            coords = itertools.chain([abs(self)], self.angles()) 
            # 配置使用尖括号显示球面坐标.
            outer_fmt = '<{}>'
        else:
            coords = self
            # 配置使用圆括号显示笛卡儿坐标.
            outer_fmt = '({})' 
        # 创建生成器表达式, 按需格式化各个坐标元素.
        components = (format(c, fmt_spec) for c in coords)
        # 把以逗号分隔的格式化分量放入尖括号或圆括号内.
        return outer_fmt.format(', '.join(components))  

    @classmethod
    def frombytes(cls, octets):
        typecode = chr(octets[0])
        memv = memoryview(octets[1:]).cast(typecode)
        return cls(memv)
    

**-------------------------------------------------------------------------------------------**
本书在__fornat__, angle 和angles中大量使用了生成器表达式,
不过这样做的目的是让Vector类的__fornat__方法与Vector2d类处在同一水平上.
第17章在讨论生成器时会使用Vector类中的部分代码举例, 详细说明生成器的技巧.
**-------------------------------------------------------------------------------------------**

本章的任务到此结束.
第16章将改进Vector类, 让它支持中缀运算符.
本章的目的是探讨如何编写容器类广泛使用的几个特殊方法.

12.9 本章小结

本章所举的Vector示例故意与Vector2d兼容, 不过二者的构造函数签名不同.
Vector类的构造函数接受一个可迭代对象, 这与内置序列类型一样.
Vector的行为之所以像序列, 是因为它实现了__getitem__方法和__len__方法.
借此, 我们讨论了协议, 这是鸭子类型语言使用的非正式接口.

然后, 本章说明了my_seq[a: b: c]句法背后的原理: 创建slice(a, b, c)对象, 交给__getitem__方法处理.
了解这一点之后, 我们让Vector正确处理切片, 像符合Python风格的序列那样返回新的Vector实例.

接下来, 本章为Vector实例的头几个分量提供了只读访问功能, 
使用的是my_vec.x这样的表示法. 这个功能通过__getattr__方法实现. 
实现这一功能之后, 用户会想通过my_vec.x=7这样的写法为头几个分量赋值--这是一个潜在的bug.
为了解决这个问题, 本章又实现了_setattr_方法, 通过它禁止为单字母属性赋值.
大多数时候, 如果定义了__getattr__方法, 那么也要定义__setattr__方法, 这样才能避免行为不一致.

实现__hash__方法特别适合使用functools.reduce函数, 
因为要把异或运算符^依次应用到各个分量的哈希值上, 生成整个向量的聚合哈希值.
在__hash__方法中使用reduce函数之后, 我们又使用内置归约函数all实现了效率更高的__eq__方法.

Vector类的最后一项改进是在Vector2d的基础上重新实现__format__方法, 
这一次, 除了支持笛卡儿坐标, 还支持了球面坐标.
为了定义__format__方法及其辅助方法, 本章用到了很多数学知识和几个生成器, 但这些是实现细节.
第17章会再次讨论生成器. 
12.7节的目的是支持自定义格式, 从而兑现承诺, 让Vector与Vector2d兼容, 此外还能做更多的事情.
与第11章一样, 本章经常分析Python标准对象的行为, 然后模仿, 让Vector的行为符合Python风格.

第16章将为Vector实现几个中级运算符, 这一章使用的数学知识比angle()方法用到的简单多了,
但是通过了解Python中缀运算符的工作方式, 我们对面向对象设计的认识将更进一步.
讨论运算符重载之前, 让我们暂且告别单个类, 来说明一下如何使用接口和继承组织多个类, 详见第13章和第14章.

12.10 延伸阅读

Vector类中的大多数特殊方法在第11章定义的Vector2d类中也有, 
因此11.14节给出的延伸阅读材料同样适合本章.

强大的高阶函数reduce的作用也可称为合拢, 累计, 聚合, 压缩和注入.
更多信息可以参见维基百科中的'Fold (higher-order function)', 
这篇文章展示了高阶函数的用途, 着重说明了具有递归数据结构的函数式语言.
另外, 这篇文章中还有一张表格, 列出了在很多编程语言中起合拢作用的函数.

"What's New in Python 2.5"简略概括了__index__的作用: 支持__getitem__方法(参见12.5.2节)
'PEP 357--Allowing Any Object to be Used for Slicing'
站在一个C语言扩展实现者(NumPy的主要创建人Travis Oliphant)的角度详细说明了需要__index__的原因.
Oliphant对Python贡献颇多, 使Python成为领先的科学计算语言,
进而使Python在机器学习应用程序中处于领先地位.

*---------------------------------------------杂谈--------------------------------------------*
'把协议当作非正式接口':
协议不是Python发明的.
Smalltalk团队, 也就是'面向对象'的发明者, 使用'协议'这个词表示现在我们称之为接口的功能.
某些Smalltalk编程环境允许程序员把一组方法标记为协议, 
但这只不过是一种文档, 用于辅助导航, 语言不对其施加特定措施.
因此, 向熟悉正式接口(编译器会施加措施)的人解释'协议'时, 我会简单地说它是'非正式接口'.

动态类型语言中的既定协议会自然进化.
所谓动态类型是指在运行时检查类型, 因为方法签名和变量没有静态类型信息.
Ruby是一门重要的面向对象动态类型语言, 它也使用协议.

在Python文档中, 如果看到'文件类对象'这样的表述, 通常说的就是协议.
这是一种简短的说法, 意思是:'行为基本与文件一致, 实现了部分文件接口, 满足上下文相关需求的东西.'

你可能觉得只实现协议的一部分不够严谨, 但是这样做的优点是简单.
<<Python语言参考手册>>中的3.3节给出了如下建议.
  模仿内置类型实现类时, 记住一点: 模仿的程度对建模的对象来说合理即可.
  例如, 有些序列可能只需要获取单个元素, 而不必提取切片.

不要为了满足过度设计的接口契约以及让编译器开心而去实现不需要的方法, 要遵守KISS原则.

然而, 如果想让类型检查工具验证协议的实现, 就要严格定义协议.
此时, 可以使用typing.Protocol.

第13章还会讨论协议和接口, 这正是那一章的主要话题.

'鸭子类型的起源':
我相信, Ruby社区在'鸭子类型'这个术语的推广过程中起到了主要作用, 他们向大量Java使用者宣扬了这个说法.
但是, 在Ruby或Python'流行'起来之前, Python就使用这种表述了.
根据维基百科, 在面向对象编程中较早使用鸭子做比喻的人是Alex Martelli,
这个比喻出现在他于2000年7月26日发到Python-list中的一条消息里.
即'polymorphism (was Re: Type checking in python?)'.
本章开头引用的那句话就出自那条消息. 
如果想知道'鸭子类型'这个术语的真正起源, 以及很多编程语言对这个面向对象概念的应用,
请阅读维基百科中的'Duck typing'词条.

'安全的__format__方法, 增强可用性':
实现__format__方法时, 我没有采取措施防范Vector实例拥有大量分量,
不过在__repr__方法中我使用reprlib做了预防.
这是因为, repr()函数用于调试和记录日志, 所以必须生成可用的输出.
而__format__方法用于向终端用户显示输出, 这些用户应该想看到整个Vector.
如果你觉得这样做危险, 那么可以再为格式规范微语言实现一个扩展.
如果是我, 我会这么做: 默认情况下, 格式化的Vector实例显示有限个分量, 比如说30个.
如果元素数量超过上限, 默认的行为是像reprlib那样, 截断超出的部分, 就使用...表示.
然而, 如果格式说明符末尾是特殊的*代码(意思是'全部'), 则不限制显示的元素数量.
因此, 用户在不知情的情况下不会被特别长的输出吓倒.
如果默认的上限碍事, 那么...的存在对用户是个提醒, 用户研究文档后会发现*格式代码.

'寻找符合Python风格的求和方式':
就像'什么是美'没有确切答案一样, '什么是Python风格'也没有标准答案.
如果回答'地道的Python'(我通常会这样说), 则不能让人100%满意,
因为对你来说是'地道的', 在我看来却可能不是.
但我可以肯定的是, '地道'并不是指使用最鲜为人知的语言功能.

Python-list中有一篇发表于2003年4月的文章, 题为'Pythonic Way to Sum n-th List Element?'
这篇文章与本章讨论的reduce函数有关.

该话题的发起人Guy Middleton说他不喜欢使用lambda表达式, 问下面的方案有没有办法改进. ⑦

(注7: 为了在此展示, 我稍微修改了这段代码, 因为在2003年, reduce是内置函数,
而在Python 3中要导入. 此外, 我把×和y两个名称换成了my_list和sub(表示子串).)

# 取2, 50, 8 相加
>>> my_list =[[1, 2, 3], [40, 50, 60], [9, 8, 7]]
>>> import functools
>>> functools.reduce(lambda a, b: a + b, [sub[1] for sub in my_list])
60

这段代码有很多地道的用法: lambda, reduce和列表推导式.
最终, 这可能会变成人气竞赛, 因为它冒犯了讨厌lambda的人和看不上列表推导式的人——这两种人可都不少.

如果打算使用lambda, 那么或许就不应该使用列表推导式--筛选除外, 但这里不是筛选.

下面是我给出的方案, 这能讨得lambda拥护者的欢心.

# 其中a是累积变量(初始值为 0), b是my_list中的一项, 使用b[1]取出了每个元素的第二个值,
# 然后将其加到a中, 最后返回累积的值.
>>> functools.reduce(lambda a, b: a + b[1], my_list, 0)
60

我没有参与那个话题, 而且不会在真实的代码中使用上述方案, 因为我非常不喜欢lambda表达式.
这里只是为了举例说明不使用列表推导式可以怎么做.
第一个答复是Fernando Perez给出的, 他是IPython的创建者, 他的答案强调了NumPy支持n维数组和n维切片.

>> import numpy as np
>>> my_array = np.array(my_list)
>>> np.sum(my_array[:, 1])
60

我觉得Perez的方案很棒, 不过Guy Middleton推崇Paul Rubin 和 Skip Montanaro给出的下述方案.

>>> import operator
>>> functools.reduce(operator.add, [sub[1] for sub in my_list], 0)
60

随后, Evan Simpson问道: '这样做有什么错?'

>>> total =0
>>> for sub in my_list:
...     total += sub[1]
>>> total
60

许多人觉得这也很符合Python风格.
Alex Martelli甚至说, Guido或许就会这么做.

我喜欢Evan Simpson的代码, 不过也喜欢David Eppstein对此给出的评论.
  如果想计算列表中各个元素的和, 那么写出的代码就应该看起来像是在'计算元素之和', 
  而不是'迭代元素, 维护一个变量t, 再执行一系列求和操作'.
  如果不能站在一定高度上表明意图, 却让语言去关注底层操作, 那还要高级语言干吗?

而后, Alex Martelli又给出了如下建议.
  '求和'是常见操作, 我不介意Python提供这样的一个内置函数.
  但是, 在我看来, 'reduce(operator.add, ...'不是好方法.
  (作为一个读过AProgramming Language的老程序员和函数式语言爱好者, 
  我应该喜欢这个方法, 但是我并不喜欢.)

随后, Alex建议提供并实现了sum()函数. 这次讨论之后3个月, Python2.3就内置了这个函数.
因此, Alex喜欢的句法变成了标准.

>>> sum([sub[1] for sub in my_list])
60

下一年年末(2004年11月)Python2.4发布了, 这一版引入了生成器表达式.
在我看来, Guy Middleton那个问题目前最符合Python风格的答案如下.

>>> sum(sub[1] for sub in my_list)
60

这样写不仅比使用reduce函数更容易理解, 而且还能避免空序列导致的: 
Sum([])的结果是0, 就这么简单.
(在使用reduce()函数时, 空序列会导致一个常见的陷阱.
具体来说, 在给定一个空序列时, reduce()函数中的累加器(即第一个参数)不会被初始化,
这可能会导致一些奇怪的错误.
例如, 如果我们试图计算空列表的和, 即 reduce(lambda x, y: x + y, [])我们会得到一个TypeError异常.

为了避免这个陷阱, 可以在reduce()函数的调用中显式提供累加器的初始值,
如reduce(lambda x, y: x + y, [], 0)中的第三个参数0就是累加器的初始值.
这样, 即使输入序列为空, 累加器也会被初始化为给定的初始值, 从而避免了错误.)

在这次讨论中, Alex Martelli指出, Python2内置的reduce函数'成事不足败事有余',
因为它推荐的地道编程方式难以理解.
他的观点最有说服力, 因此Python3把reduce函数移到了functools模块中.
当然, functools.reduce函数仍有用武之地.
实现Vector.__hash__方法时我就用了它, 我觉得我的实现方式算得上符合Python风格.