【贪心算法】之 摆动序列（中等题）

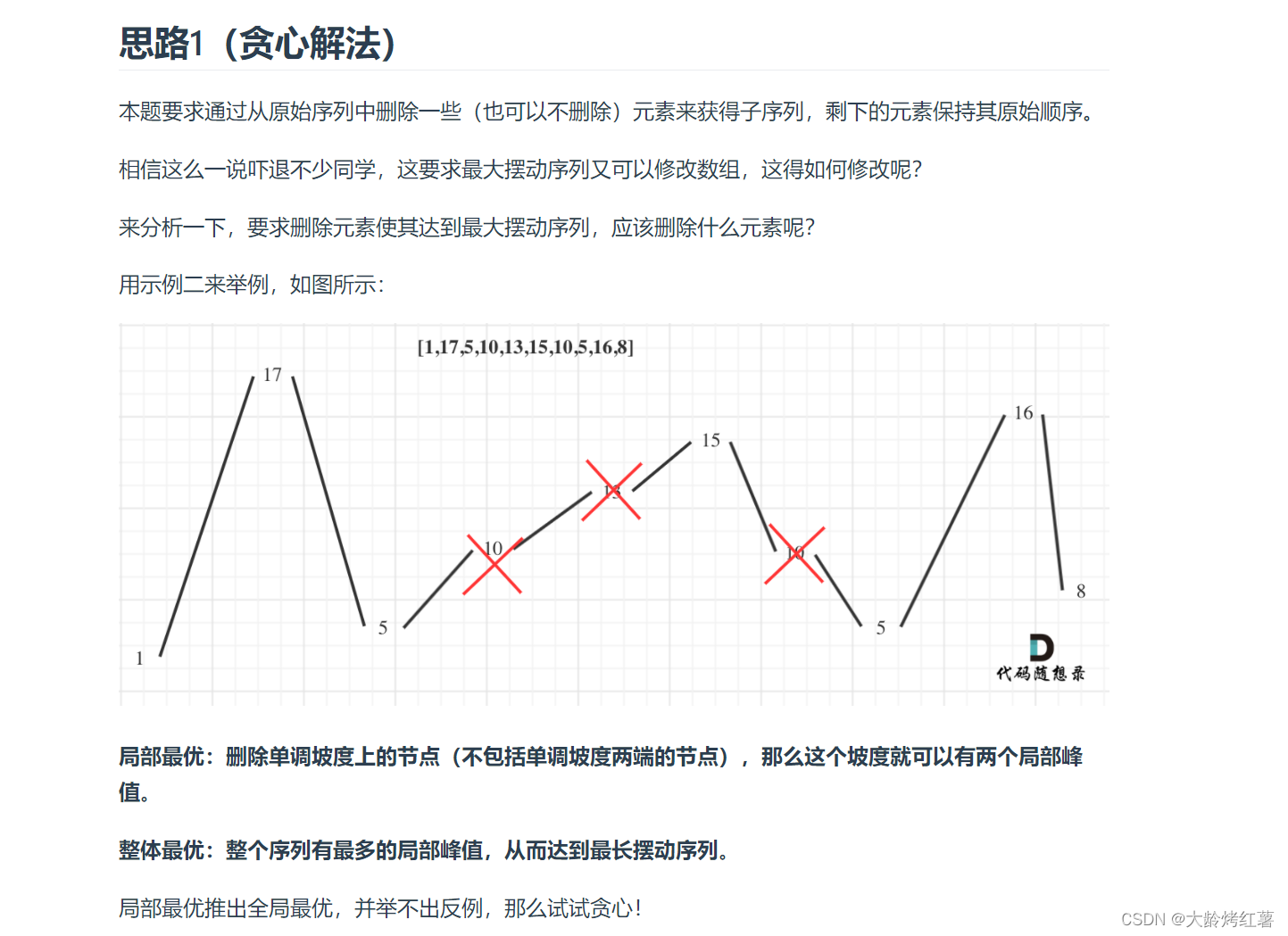
实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）

这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点。

也就是说前一个和后一个若是有峰值index就++；

贪心代码一：

 public static int wiggleMaxLength(int[] nums) {
        int index=1;//记录峰值个数 默认最右边有一个
        int pre=0;
        int curr=0;
        if (nums.length<=1){
            return nums.length;
        }
        for (int i = 0; i <nums.length-1 ; i++) {
            curr=nums[i+1]-nums[i];
            //等于0的情况表示初始时的pre
            if ((curr>0 && pre<=0) || (curr<0 && pre>=0)){
                index++;
                pre=curr;
            }
        }
        return index;
    }

贪心代码二：

    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        if (n < 2) {
            return n;
        }
        int prevdiff = nums[1] - nums[0];
        int ret = prevdiff != 0 ? 2 : 1;//理解 若是第一对（比如 2 2 5），差值为0，则就舍去其中一个2，此时峰值就一个2；
        //若是！=0 eg：2 3 1，则峰值就两个2，3
        for (int i = 1; i < n-1; i++) {
            int diff = nums[i+1] - nums[i];
            if ((diff > 0 && prevdiff <= 0) || (diff < 0 && prevdiff >= 0)) {
                ret++;
                prevdiff = diff;
            }
        }
        return ret;
    }

个人认为此题最优化的解法（动态规划）：

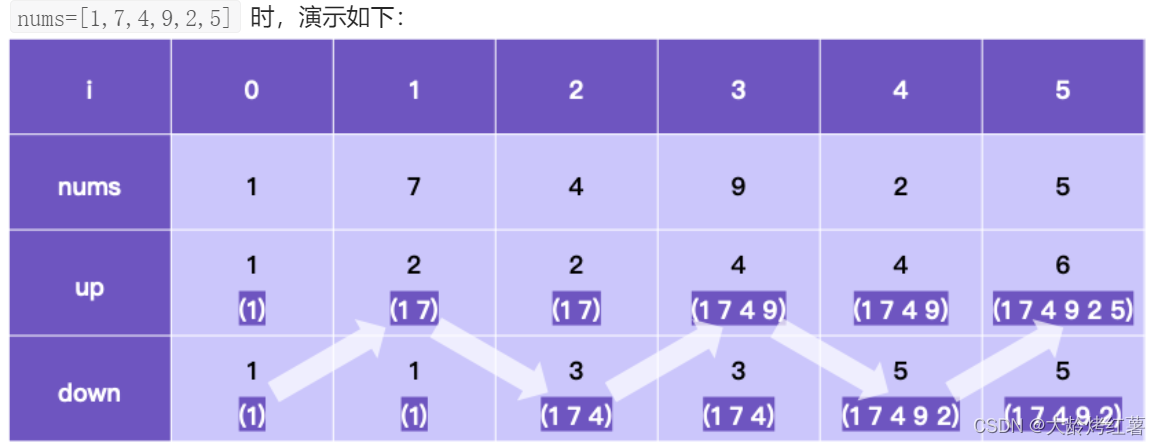
既然是摆动序列我们就摆起来up上升，down下降，eg：当为 1 7 8 9 2 5时候，因为后面的值在i=3之前一直大于前面的值，所以down一直=1；在=8时候，up=down+1 依旧=2，=9时候，up=down+1 仍然=2；直到=2时，num[i]<nums[i-1]了，此时down=up+1=3；然后下一个是 >，up=down+1=3+1=4；最大摆动序列长度就是4 。（1 7 2 5）

public int wiggleMaxLength(int[] nums) {
    if(nums.length<=1){
        return nums.length;
    }
    int down = 1, up = 1;
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] > nums[i - 1]){
            up = down + 1;
        }else if (nums[i] < nums[i - 1]){
            down = up + 1;
        }
    }
    return Math.max(down, up);
}