DP进阶之路——不同路径问题

不同路径

62.?不同路径

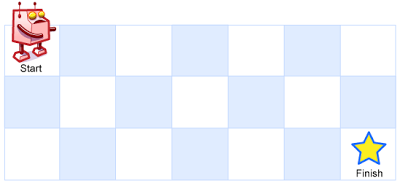
一个机器人位于一个?m x n?网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

我们可以已知的是，其实动态规划是一种从dfs开始-》dfs剪枝 -》动态规格的优化过程。

这个题目其实我们可用dfs尝试?

class Solution {
    int cnt =0;
    public int uniquePaths(int m, int n) {
        dfs(m-1,n-1,0,0);
        return cnt;
    }
    void dfs(int m,int n,int x,int y){
        if(x == m && y == n)    {
            cnt++;
            return;
        }
        if(x > m || y>n)    return;

        dfs(m,n,x+1,y);
        dfs(m,n,x,y+1);
    }
}

?尝试之后我们会发现，时间超限

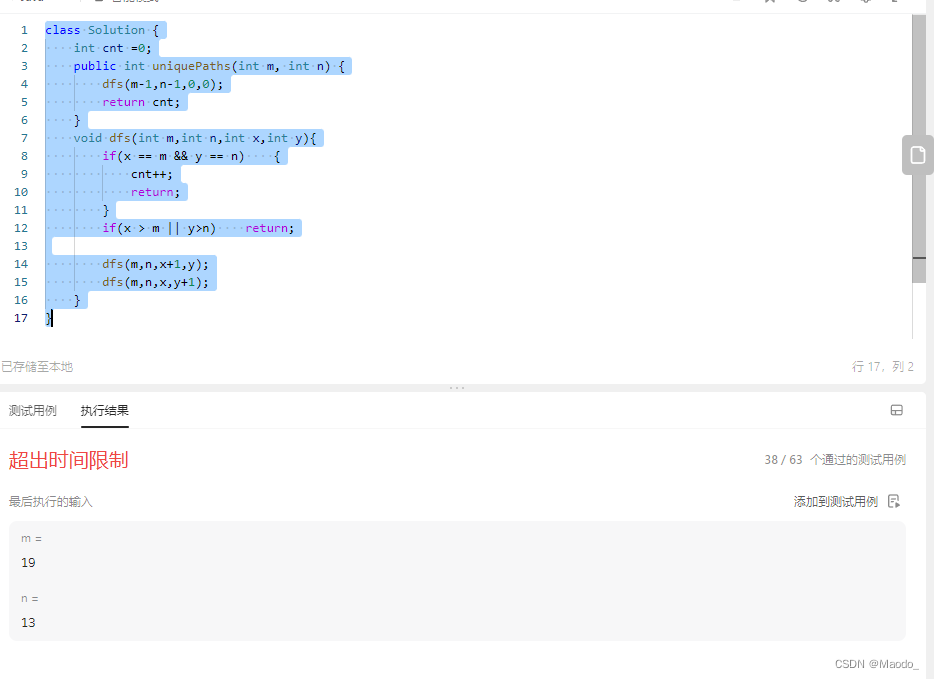
so，我们可以开始通过剪枝优化（剪枝其实就是记录重复项了，减少对重复项的运行了）

?

class Solution {
    int[][] memo;
    public int uniquePaths(int m, int n) {
        memo = new int[m][n];
        return dfs(m-1, n-1, 0, 0);
    }
    
    int dfs(int m, int n, int x, int y) {
        if (x == m || y == n) {
            return 1; // 边界情况，只有一条路径
        }
        
        if (memo[x][y] > 0) {
            return memo[x][y]; // 如果已经计算过，则直接返回结果
        }

        int right = dfs(m, n, x + 1, y); // 向右走的路径数
        int down = dfs(m, n, x, y + 1); // 向下走的路径数
        
        memo[x][y] = right + down; // 将计算结果存入备忘录
        
        return memo[x][y];
    }
}

然后提交，运行，然后发现过了。但是我们可不仅仅追求这些，我们要的是dp

在这里了，我们就可以通过上述的memo数组找出它的递推公式了。

如果我们要到meoo[i][j] 这个节点，只有两种路径可以到达。

上面节点向下，或者是左边节点向右到达

递推公式：

memo[i][j] = memo[i-1][j] + memo[i][j-1]

?

?

?

然后就是确定dp数组初始值的问题了，我们不难发现如果一直向左或下，那这里永远只是一条路径。

所以可以确定：

这里的初始值是1

?

????????int[][] dp = new int[m][n];

? ? ? ? for(int i=0;i<m;i++) ? ?dp[i][0] = 1;

? ? ? ? for(int i=0;i<n;i++) ? ?dp[0][i] = 1;

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        //初始值
        for(int i=0;i<m;i++)    dp[i][0] = 1;
        for(int i=0;i<n;i++)    dp[0][i] = 1;

        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];//递推公式运行
            }
        }
        return dp[m-1][n-1];
    }
}

?

不同路径2

63.?不同路径 II

一个机器人位于一个?m x n?网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用?1?和?0?来表示。

示例 1：

?

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有2条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

?这里题目其实同上面第一题思路是一样的，不同的只有一个，当有石头挡路的时候就不走那边了

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int n = obstacleGrid.length;
        int m = obstacleGrid[0].length;
        int[][] dp = new int[n][m];
        
        dp[0][0] = obstacleGrid[0][0] == 1 ? 0 : 1; // 如果起点有障碍物，则无法到达，路径数为0
        for (int i = 1; i < n; i++) {
            dp[i][0] = obstacleGrid[i][0] == 1 ? 0 : dp[i - 1][0];
        }
        for (int i = 1; i < m; i++) {
            dp[0][i] = obstacleGrid[0][i] == 1 ? 0 : dp[0][i - 1];
        }
        
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                if (obstacleGrid[i][j] == 1) {
                    dp[i][j] = 0; // 如果当前位置有障碍物，则无法到达，路径数为0
                } else {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[n - 1][m - 1];
    }
}