Codeforce s Round 920 (Div. 3) G题 旋转矩阵，斜缀和，平移

Problem - G - Codeforces

目录

题意：

思路：

总思路：

旋转矩阵：

前缀和预处理：

平移的处理，尤其是越界的处理：

核心代码：

---

题意：

给你个n*m的矩阵，里面要么是目标' # '，要么是空的' . '。

还有值k，代表这样的范围: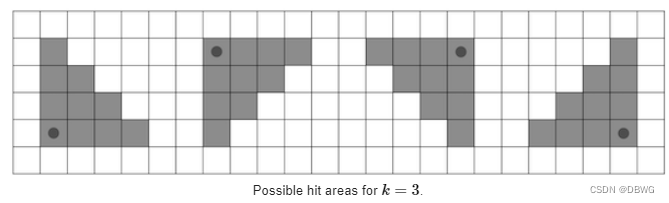

我们有四个方向可选。图中黑点即是我们落脚点，可以随意选，要使黑色区域的目标'#'最多，输出这个最大值

思路：

总思路：

‘#’是随机给的，我们只能暴力。暴力上做优化即可。

如果这四种都做，代码是类同但细节处理太多，而只用一种方向然后旋转矩阵这样是等价的。

我们选择第三种，使用前缀和（列缀和，斜缀合）方便：

由于面积可能很大，每个落脚点都数时间消耗太多。我们可以发现相邻的是平移过去的，只差一列和斜着一列：

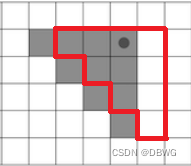所以我们对上次的‘#’数目，加上这列的'#'数目，再减去斜着的'#'数目，就是这次的'#'数目了。

预处理出前缀和，这样平移时加的减的都可以直接算出来。（越界的处理需要注意）

旋转矩阵：

（这个C语言OJ就写过。我好像有一次没写出来，然后就有了心理阴影，其实很好写）

我们再创个二维char数组next，把旋转的写进这个数组，然后覆盖原数组即可。

我们可以借助个例子去想，比如顺时针旋转：

1 2 3 4      5 1		
5 6 7 8	     6 2
	         7 3
	         8 4

我们可以发现第一行变成了倒数第一列，而原来的列数变成了新的行数。

所以next[ j ][ chars.size()-1-i?] = chars[ i ][ j ]? ? ? ? (chars就是原始图）

vector<vector<char>>next(chars[0].size(), vector<char>(chars.size()));
for (int i = 0; i < chars.size(); i++)
{
	for (int j = 0; j < chars[0].size(); j++)
	{
		next[j][chars.size()-1 - i] = chars[i][j];
	}
}
chars = next;

（注意新的图的n和m是变的。）

前缀和预处理：

可能没写过斜缀和。然后下标可以从1开始，我是写的从0开始的。

	int t = 4;
	while (t--)
	{
		n = chars.size(), m = chars[0].size();
		vector<vector<int>>narr(n, vector<int>(m)), rd(n, vector<int>(m));
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < m; j++)
			{
				if (i > 0)
					narr[i][j] = narr[i - 1][j] + (chars[i][j] == '#');
				else
					narr[i][j] = chars[i][j] == '#';
			}
		}
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < m; j++)
			{
				if(i>0&&j>0)
					rd[i][j] = rd[i - 1][j - 1] + (chars[i][j] == '#');
				else
					rd[i][j] = chars[i][j] == '#';
			}
		}

平移的处理，尤其是越界的处理：

for (int i = 0; i < n; i++)
{
	int tmp = narr[min(i + k, n - 1)][0] - (i - 1 >= 0 ? narr[i - 1][0] : 0);
	ans = max(ans, tmp);
	for (int j = 1; j < m; j++)//右平移
	{
		//x,y:前一个位置最下面那个点
		int x = i + k, y = j-1;
		if (x >= n)
		{
			y -= x - (n - 1);
			x = n - 1; 
		}
		tmp += narr[min(i+k,n-1)][j] - (i - 1 >= 0 ? narr[i - 1][j] : 0);
		if(y>=0)
		tmp	-= rd[x][y] - (j - 1 - k - 1 >= 0&&i-1>=0 ? rd[i - 1][j - 1 - k - 1] : 0);
		ans = max(ans, tmp);
	}
}

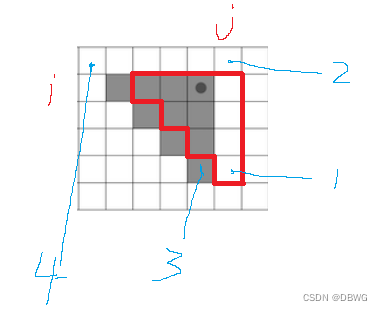代码中x,y就是1点。

1的列缀合-2的列缀合就是新增的'#'

3的斜缀合-4的斜缀合就是失去的'#'

最难处理的就是3越界后的斜缀合：

我们可以发现，不管下面什么情况越界，最后一行都是n-1。我们取n-1对应着的斜缀合即可。

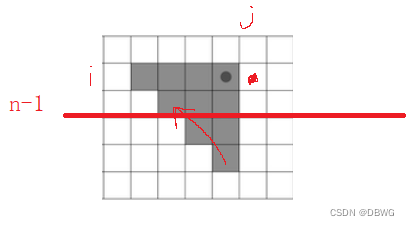
x,y仍代表1点（见上面），(x,y-1)就是原来的斜缀合的点，现在往左上角移动了，行的变换数是等于列的变换数的，而行变换（x-(n-1)），那么列也减去这个，即行为n-1，列为y-1 - (x-(n-1))。

其余的越界是好处理的，代码里有我的处理情况。

核心代码：

void solve()
{
	int n, m, k;
	cin >> n >> m >> k;
	vector<vector<char>>chars(n, vector<char>(m));
	for (int i = 0; i < n; i++)
		for (int j = 0; j < m; j++)
			cin >> chars[i][j];

	int ans = 0;
	int t = 4;
	while (t--)
	{
		n = chars.size(), m = chars[0].size();
		vector<vector<int>>narr(n, vector<int>(m)), rd(n, vector<int>(m));
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < m; j++)
			{
				if (i > 0)
					narr[i][j] = narr[i - 1][j] + (chars[i][j] == '#');
				else
					narr[i][j] = chars[i][j] == '#';
			}
		}
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < m; j++)
			{
				if(i>0&&j>0)
					rd[i][j] = rd[i - 1][j - 1] + (chars[i][j] == '#');
				else
					rd[i][j] = chars[i][j] == '#';
			}
		}

		for (int i = 0; i < n; i++)
		{
			int tmp = narr[min(i + k, n - 1)][0] - (i - 1 >= 0 ? narr[i - 1][0] : 0);
			ans = max(ans, tmp);
			for (int j = 1; j < m; j++)//右平移
			{
				//x,y:前一个位置最下面那个点
				int x = i + k, y = j-1;
				if (x >= n)
				{
					y -= x - (n - 1);
					x = n - 1; 
				}
				tmp += narr[min(i+k,n-1)][j] - (i - 1 >= 0 ? narr[i - 1][j] : 0);
				if(y>=0)
				tmp	-= rd[x][y] - (j - 1 - k - 1 >= 0&&i-1>=0 ? rd[i - 1][j - 1 - k - 1] : 0);
				ans = max(ans, tmp);
			}
		}

		vector<vector<char>>next(chars[0].size(), vector<char>(chars.size()));
		for (int i = 0; i < chars.size(); i++)
		{
			for (int j = 0; j < chars[0].size(); j++)
			{
				next[j][chars.size()-1 - i] = chars[i][j];
			}
		}
		chars = next;
	}
	cout << ans << endl;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t; cin >> t;
	while (t--)
	{
		solve();
	}
	return 0;
}