初学dfs深度优先搜索&洛谷【 八皇后 Checker Challenge】题解

我对深度优先搜索（DFS）的理解

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。这种算法会尽可能深地搜索一条通路，当搜索到某节点的所在边都己被探寻过时，搜索将回溯到发现该节点的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

简单的来说dfs就是一路走到黑，将走过的路标记为不可走，无路可走时才回退一步继续寻找可走的路。

我们总能通过这个算法找到一条通往终点的路（这条路很可能不是最短的），或者告诉自己根本没有哪条路能通往终点。

洛谷【 八皇后 Checker Challenge】题解

原题点这里-->P1219 [USACO1.5] 八皇后 Checker Challenge - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

?八皇后问题是一道十分经典的dfs求解题，写完这道题使我对dfs有了进一步的理解。

题目描述

一个如下的?6×66×6?的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

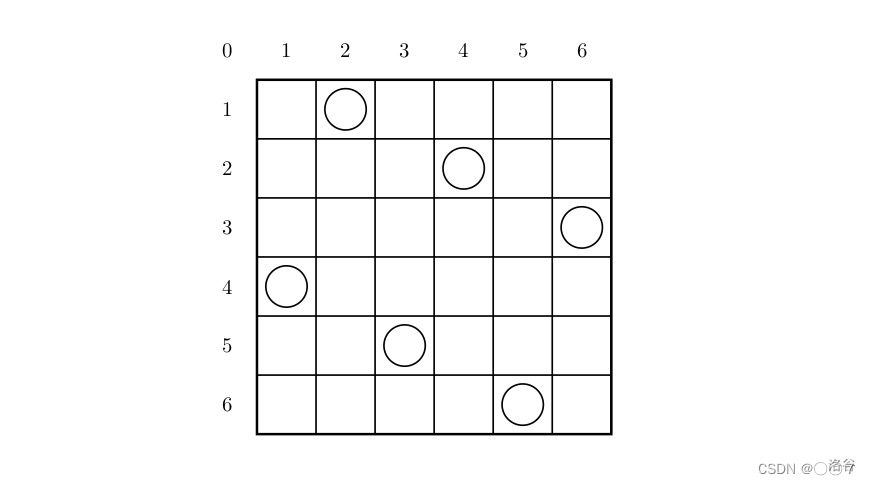
上面的布局可以用序列?2?4?6?1?3?52?4?6?1?3?5?来描述，第?i?个数字表示在第?i?行的相应位置有一个棋子，如下：

行号?1?2?3?4?5?61?2?3?4?5?6

列号?2?4?6?1?3?52?4?6?1?3?5

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前?33?个解。最后一行是解的总个数。

输入格式

一行一个正整数?n，表示棋盘是?n×n?大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例

输入 #1

6

输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

说明/提示

【数据范围】
对于?100%?的数据，6≤n≤13。

源代码

解题思路参考代码注释

#include<stdio.h>

int y[15],n,sum; 
//数组用于记录每一行棋子的纵坐标，n为棋盘大小，sum用于记录解的总数 

void dfs(int step)//深度优先搜索 
{
	if(step==n+1)//step为n+1表示n颗棋子已按要求摆放完
	{
		sum++;//总数+1 
		if(sum<=3)//输出前三种答案 
		{
			for(int i=1;i<=n;i++)
			printf("%d ",y[i]);
			printf("\n"); 
		}
		return;	
	} 
	
	for(int i=1;i<=n;i++)//for循环遍历，深度优先搜索主体 
	{
		int k=0;//用于判断位置是否可用  
		for(int j=1;j<step;j++)
		{
			if(i==y[j]||step-j==i-y[j]||step-j==y[j]-i)//若与step前第j个棋子同列或同斜线 
			{
				k=1;//该位置不可用 
				break;
			}
		}
		if(k)
		continue;
		
		y[step]=i;
		dfs(step+1);
	} 
	return;//该级结束，返回上一级 
}
  
int main()
{
	scanf("%d",&n);//由题输入n 
	dfs(1);//step从1开始 
	printf("%d",sum);
	return 0;
}

?在编写dfs（）函数时主要注意两个点，一是调用（进入下一级，即for循环部分），二是返回（返回上一级，即if部分和最后的return）。为防止出错，我们把if放在for循环前面，先判断是否满足返回条件再考虑下一级函数的调用。

总结

深度优先搜索中包含了对栈的运用，我们要特别注意函数的调用和回溯部分以及函数返回的条件。

如果你没有在这篇初学者写的文章里发现错误，请点个赞，

若你在浏览时发现了任何不当，请留言指出，并点个赞。

都看到这里了，点个赞再走咯。