[ACM算法学习] 诱导排序与 SA-IS算法

学习自诱导排序与SA-IS算法 - riteme.site

为了简化一些操作，定义 # 是字典序最小的字符，其字典序小于字母集里任意字符，并且将其默认作为每个字符串的最后一个字符，即作 S[|S|]

SA-IS 算法

SA-IS 算法是基于诱导排序这种思想。基本思想就是将问题的规模缩小，通过解决更小的问题，获取足够信息，就可以快速的解决原始问题。所以，这一过程需要递归处理子问题。

算法基本框架：

问题一个一个来解决

后缀类型

从后往前来看的话，如果当前字符 i 比后一个字符 i+1 字典序小，当前字符为S型；

如果当前字符 i 比后一个字符 i+1 字典序大，当前字符为L型；

如果当前字符 i 与后一个字符 i+1 字典序相同，则延续 i+1 的类型。

LMS子串

#单独作为一个平凡的 LMS 子串，一串S型最靠左的那个为*型，两个*型字符（包括这两具字符）之间的子串，就是LMS子串。

对于引理2.7，真前缀的前缀不是说是原字符的前缀，而是说SL串的类型的前缀。

对LMS子串进行排序

基数排序，参考字符串之————基数排序（LSD、MSD） - 就像空中月 - 博客园 (cnblogs.com)

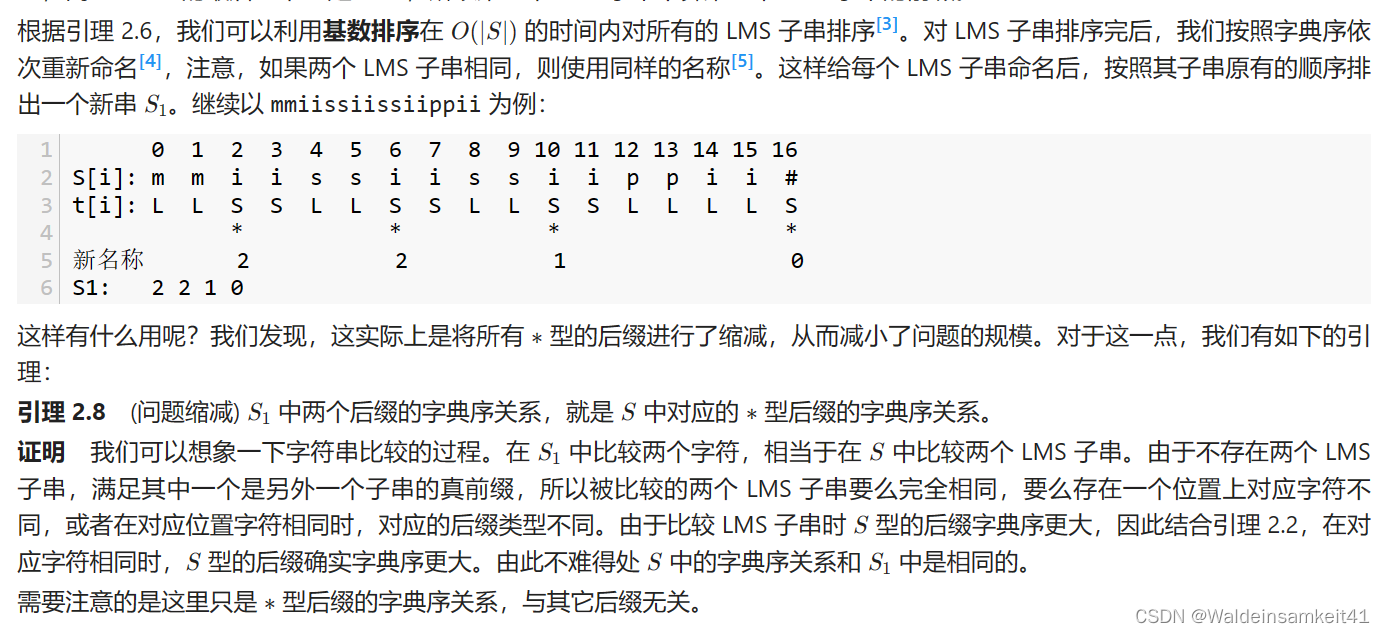
用基数排序对 LMS 子串进行排序后，再重新命名（相同的子串命相同名称），按照子串原有的顺序排出一个新串 S1 （内容是新命名）。

从SA1诱导至SA

可行性：S1的后缀数组SA1，可以得到所有*型后缀的字典顺序，如果利用*型后缀的字典顺序来对其它的L型和S型后缀进行排序，就可以完成后缀数组的计算。

可以发现：

• 首字母相同的后缀是连续排布的
• S?型或?L?型会连续分布，因为：如果后缀类型不同，则相对顺序是确定的。因此易知不会出现?S?型和?L?型交替出现的情况。更进一步，由于?L?型后缀更小，因此总是先排布?L?型后缀，再排布?S?型后缀。

我们可以利用桶排序的思想，为每一个出现过的字符建立一个桶，用?SA?数组来存储这些桶，每个桶之间按照字典序排列，这样就可以使后缀数组初步有序。因此每一个字符的桶可以分为两部分，一个用于放置?L?型后缀，另一个则用于?S?型后缀。为了方便确定每一个桶的起始位置，S?型后缀的桶的放置是倒序的。

但是如果首字母和后缀类型都一致，我们不能直接快速地判断大小关系。在这里就要利用到诱导排序了。