【教学类-43-17】4宫格数独、9宫格数独（2*2、3*3可算全部数字）

作品展示：

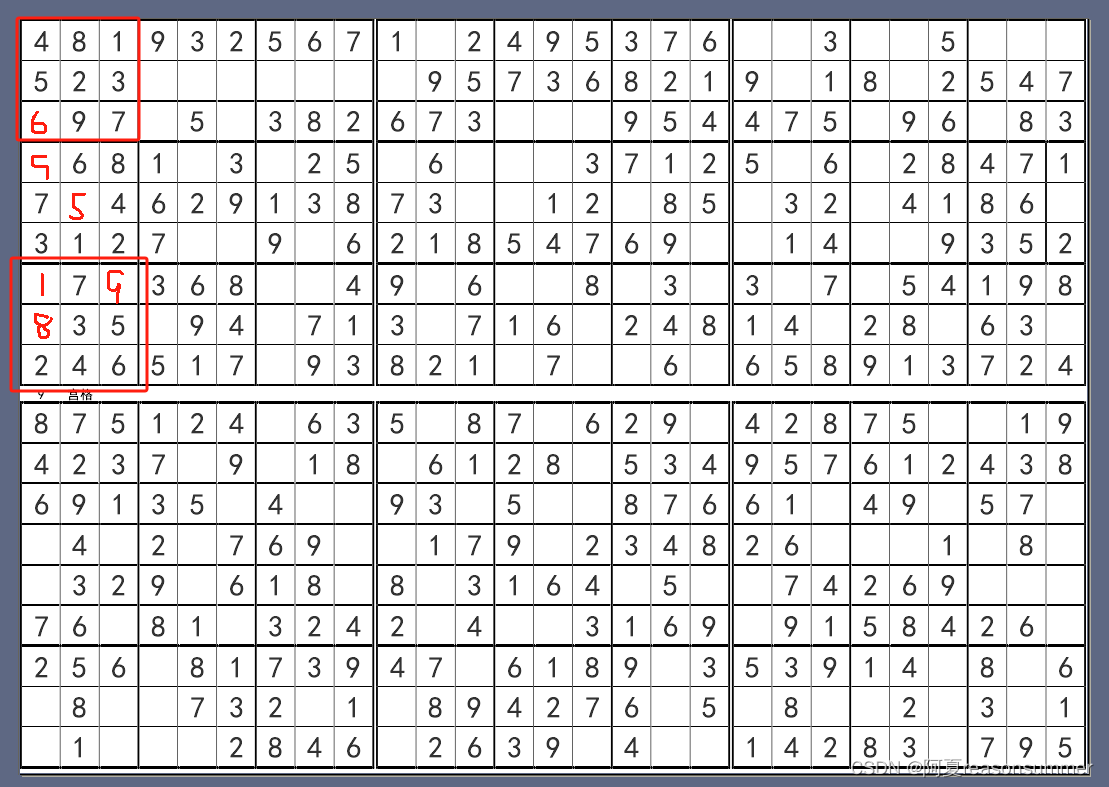
4宫格 2*2格子里包含1-4

9宫格3*3格子里包含1-9

?

?

背景需求：

大4班 一位男孩做9宫格数独题：提出质疑：“这个数独题有问题，！”

“不会有问题，这是电脑程序写出来的”

他没有申辩，又拿了几张5宫格，完成后再次做那张9宫格

?

然后我走到他身边拍照时，他再次提出：”这个题目有问题，算不出！“

”哪里有问题？“我问

他说不上来，再次强调：”我家里的数独题不是这个样子的！这个有问题的！“

我突然想起了九宫格”3*3“小格里必须填满1-9数字的1.0版规则，于是指着左上角的3*3格子问他

“你是不是说，”这里的9个格子应该是填满1-9的“

”嗯“他点头，”就是这样！这个没法填！”

“你说的对，其实九宫格数独除了横向 和纵向 推算数字，还有一个方法就是这种3*3格子里的填写，这个小格子里面都有2个1，肯定是不对的，没法凑满1-9，但是我这份里面只能横向和纵向推算。”

“那这个就不对了！”

“嗯，这是另一种9宫格数独题，你可以试试，只能横着、竖着算！9个小格子就别看了！”

最后结束时，这套只能横向、纵向推算的九宫格题还真被他完成了！

?

思考：

这位男孩有9宫格数独的经验，因此知道正确的9宫格是3*3格子9套组成的，最初我也是用生成样式的代码制作的9宫格，但是它不能通用3-8宫格，所以把代码修改成只能横纵判断的样式

而且我发现真正能够让小格子包含所有的数字的只有4宫格（2*2=4）和9宫格（3*3=9），数量很少。

今天大四班男孩的提问，让我发现9宫格样式需要包含小格子判断的元素。

结论：

因此投放4宫格、9宫格数独时，应该使用1.0的代码（考虑小格子包含所有数字、考虑横纵）

【教学类-43-01】20231226 九宫格数独1.0「作者：Vaeeeeeee」（每张基础位置都不同）-CSDN博客文章浏览阅读404次，点赞7次，收藏7次。【教学类-43-01】20231226 九宫格数独1.0「作者：Vaeeeeeee」（每张基础位置都不同）https://blog.csdn.net/reasonsummer/article/details/135231228

在3、5、6、7、8宫格时，采用10.0的样式（只考虑横纵，小格子无法包含所有数字）

【教学类-43-12】A4最终版 20231231 数独10.0 N宫格X*Y=Z套(n=3-9)，套用不同的A4横版模板-CSDN博客文章浏览阅读380次，点赞7次，收藏9次。【教学类-43-12】A4最终版 20231231 数独10.0 N宫格X*Y=Z套(n=3-9)，套用不同的A4横版模板https://blog.csdn.net/reasonsummer/article/details/135317922

素材准备：

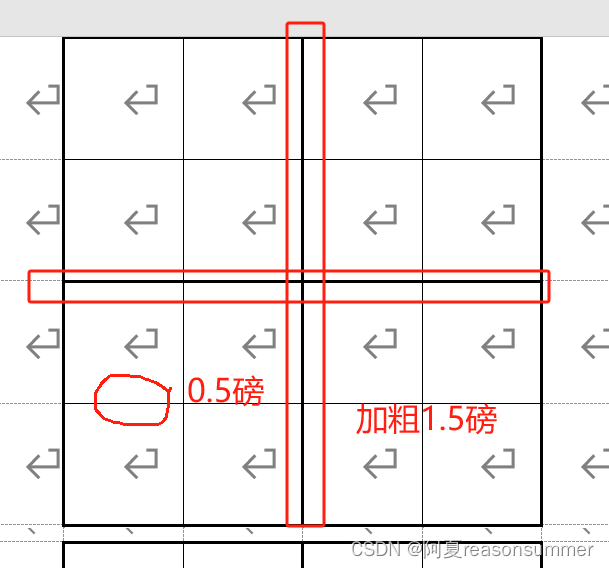
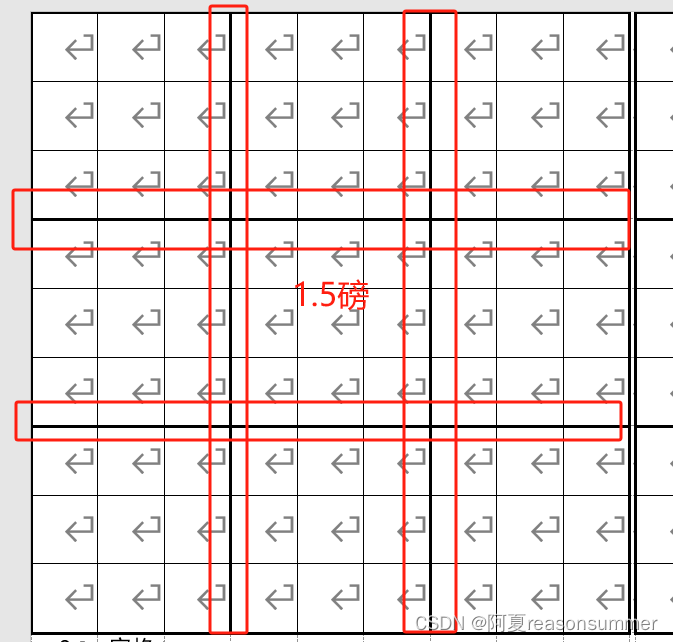
对A4的4宫格、9宫格模板进行修改，将它画成小格子

中线加粗

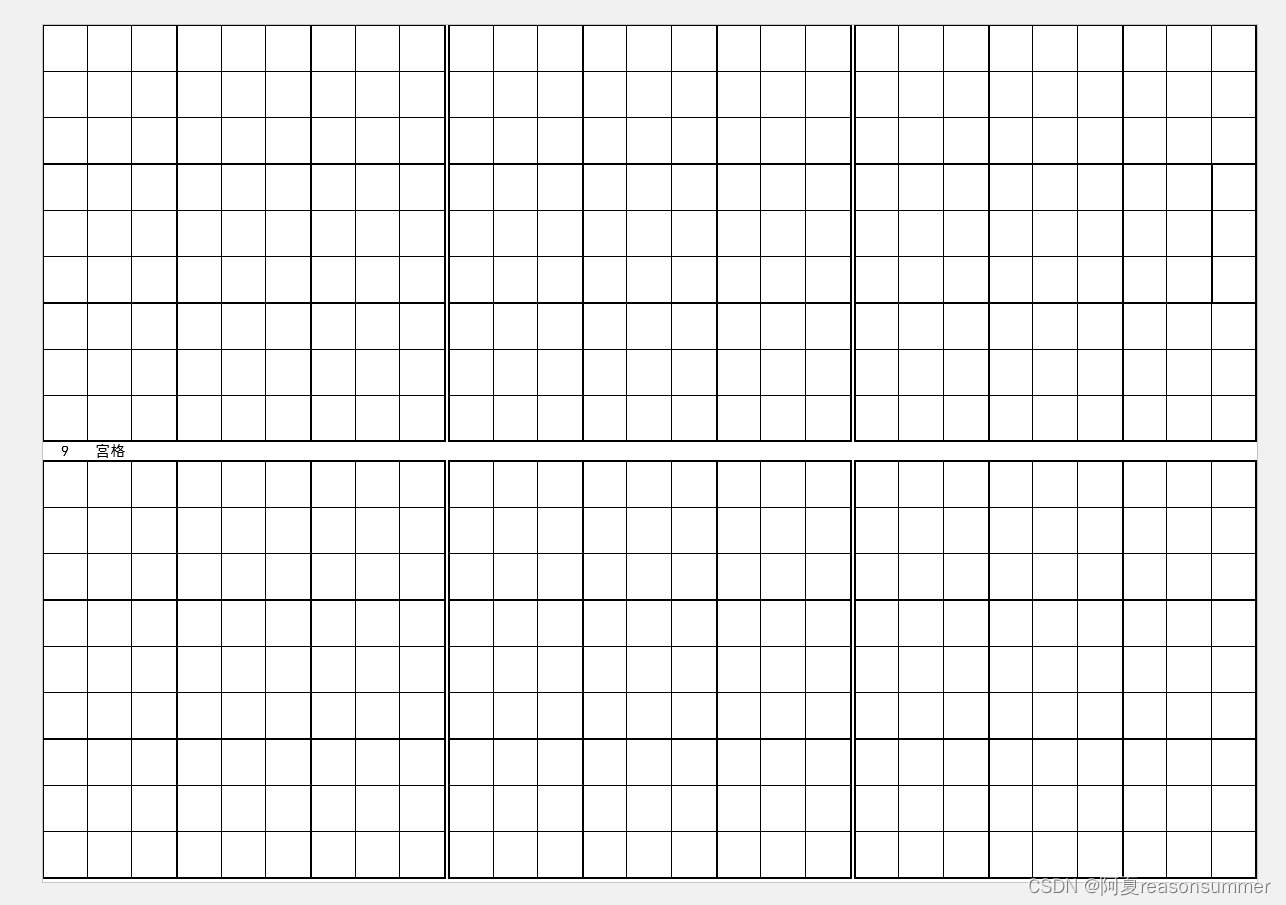
4宫格 一页12个

?

9宫格 一页6个

代码展示：

# 测试11*11格，2*2一共4套3*3 宫格
'''
目的：数独21 九宫格3小格正好等于1-9，4宫格2小格正好等于1-4，套用A4横版模板6套.控制空格数量
作者：阿夏（参考）
时间：2024年1月10日 13:35



'''

import random
from win32com.client import constants,gencache
from win32com.client.gencache import EnsureDispatch
from win32com.client import constants # 导入枚举常数模块
import os,time

import docx
from docx import Document
from docx.shared import Pt 
from docx.shared import RGBColor
from docx.enum.text import WD_PARAGRAPH_ALIGNMENT
from docx.oxml.ns import qn


from docxtpl import DocxTemplate
import pandas as pd
from docx2pdf import convert
from docx.shared import RGBColor


# 生成题库
import random
import copy

num=int(input('生成几份\n'))
# 制作"单元格"# 几宫格
hsall=int(input('请输入4或9\n'))
hs=hsall

kk=int(input('空格数量，输入5，就是50%，就是空一半）\n'))

# 因为有3-9的不同word模板，其中3-4模板一页生成9套，5-9模板一页生成6套，这里直接生成边长

ll=['4','9'] # 如果输入345
mm=['43','32']# 3对应的套数是4*3套
nn=['24','24']# 3对应的写入单元格的数字大小36磅 
for r in range(len(ll)):
    if hsall ==int(ll[r]):
        # 底边几套.底边看有2份
        db=int(mm[r][0])
        # int(input('底边几套? 3\n'))
        # 侧边几套 侧边看也是2份
        print(db )        
        cb=int(mm[r][1])
        # int(input('侧边几套? 2\n'))
        print(cb)
        size=int(nn[r])
        print(size)        # 写入单元格数字的大小（撑满格子）

# 新建一个”装N份word和PDF“的临时文件夹
imagePath1=r'C:\Users\jg2yXRZ\OneDrive\桌面\数独\零时Word'
if not os.path.exists(imagePath1):  # 判断存放图片的文件夹是否存在
    os.makedirs(imagePath1)  # 若图片文件夹不存在就创建

# 计算不同模板中的单元格坐标，放在bg里
# 棋盘格子数量，

# 如果正方形：底边2*侧边2，就是3*3宫格 2*2=4套，底边边格子数量就是3*2+1=7，侧边格子数量就是3*2+1=7，
# 如果长方形：底边3*侧边2，就是3*3宫格，3*2=6套 底边格子数量就是3*3+2=11，侧边格子数量就是3*2+1=7，
# if db==cb:
db_size = hs*db+db-1
cb_size=  hs*cb+cb-1
print('{}宫格排列底{}侧{}共{}套,底边格子数{}'.format(hs,db,cb,db*cb,db_size ))
print('{}宫格排列底{}侧{}共{}套,侧边格子数{}'.format(hs,db,cb,db*cb,cb_size ))

# 确定每个宫格的左上角坐标 00 04 40  44
bgszm=[]
for a in range(0,cb_size,hs+1):    # 0-11每隔4，写一个坐标  侧边y
    for b in range(0,db_size,hs+1):  # 0-11每隔4，写一个坐标  侧边x
        bgszm.append('{}{}'.format('%02d'%a,'%02d'%b))
print(bgszm)
# 3宫格排列底3侧2共6套,底边格子数11
# 3宫格排列底3侧2共6套,侧边格子数7
# ['0000', '0004', '0008', '0400', '0404', '0408']
    

# 转为元祖
start_coordinates = [(int(s[0:2]), int(s[2:4])) for s in bgszm]
cell_coordinates = []

# 推算每个起始格子后面的单元格数字
for start_coord in start_coordinates:
    i, j = start_coord
    subgrid_coordinates = []
    for x in range(hs):
        for y in range(hs):
            subgrid_coordinates.append((i + x, j + y))
    cell_coordinates.append(subgrid_coordinates)

# 打印结果（元祖样式）
bg=[]
for coordinates in cell_coordinates:
    # print(coordinates)     # [(4, 8), (4, 9), (4, 10), (5, 8), (5, 9), (5, 10), (6, 8), (6, 9), (6, 10)]
    for c in  coordinates:
        print(c)        # 元组 (1, 2) 样式
        s = ''.join(str(num).zfill(2) for num in c)   # zfill将元组 (1, 2) 转换为字符串 '0102' 特别是（5,10）这种必须转成2个数字0510
        print(str(s))        #  '12'
        bg.append(s)  #  '0102'
print(bg)


# 生成PDf
P=[] 
for z in range(num):  
    P.clear()
    #    制作4份数据
    for j in range(db*cb):    #  3宫格，4*3=12套
       
        # ————————————————
    # 版权声明：本文为CSDN博主「Vaeeeeeee」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
    # 原文链接：https://blog.csdn.net/m0_46366547/article/details/131334720
        def generate_sudoku_board():
            # 创建一个9x9的二维列表，表示数独棋盘
            board = [[0] * hs for _ in range(hs)]

            # 递归函数，用于填充数独棋盘的每个单元格
            def filling_board(row, col):
                # 检查是否填充完成整个数独棋盘
                if row == hs:
                    return True
                
                # 计算下一个单元格的行和列索引
                next_row = row if col < hs-1 else row + 1
                next_col = (col + 1) % hs

                import math

                r = int(math.sqrt(hs))
                print(r)

                # 获取当前单元格在小九宫格中的索引
                box_row = row // r
                box_col = col // r

                # 随机生成1到9的数字
                numbers = random.sample(range(1, hs+1), hs)

                for num in numbers:
                    # 检查行、列、小九宫格是否已经存在相同的数字
                    if num not in board[row] and all(board[i][col] != num for i in range(hs)) and all(num != board[i][j] for i in range(box_row*r, box_row*r+r) for j in range(box_col*r, box_col*r+r)):
                        board[row][col] = num

                        # 递归填充下一个单元格
                        if filling_board(next_row, next_col):
                            return True

                        # 回溯，将当前单元格重置为0
                        board[row][col] = 0

                return False

            # 填充数独棋盘
            filling_board(0, 0)
            return board
        
        # 这一块是按照等级随机产生空格，数量不稳定，    
        # def create_board(level): # level数字越大代表游戏难度越大,空白格子越多
        #         """
        #         生成一个随机的数独棋盘,空白格少
        #         """
        #         board = generate_sudoku_board()
        #         board1 =  copy.deepcopy(board)
        #         for i in range(hs*hs):
        #             row = i // hs
        #             col = i % hs
        #             if random.randint(0, hs) < level:   # 随机数量
        #                 board1[row][col] = 0                          # 格子填充为0
        #         return (board,board1)
        
        # if hs==9:
        #     v = create_board(5)[1]  
        #     print(v)
        # if hs==4:
        #     v = create_board(3)[1]  
        #     print(v)

        # 定量出现空白格子
        def create_board(): # level数字越大代表游戏难度越大
            """
            生成一个随机的数独棋盘,空白格少
            """
            board = generate_sudoku_board()
            board1 =  copy.deepcopy(board)

            blanks = random.sample(range(hs*hs), int(hs*hs*kk/10))
            for i in blanks:
                row = i // hs
                col = i % hs
                board[row][col] = 0

                    
                # if random.randint(0, hs) < level:
                #     board1[row][col] = 0
            return board

        v = create_board() 

        # 数字越小，空格少
        # 数字大，空格多
            
        # 这里无法控制空格的数量


                
        # 提取每个元素
        

        for a1  in v:         # 第一次读取，[a,b][c,d][e,f]的内容-列表
            for a2 in a1:    # 第二次读取，[a,b,c,d,e,f]的内容-元素
                if a2==0:                # 如果某个元素==0，就替换成空
                    P.append('')
                else:      # 如果某个元素非0，就写入本身的数字
                    P.append(a2)
        print(P)
        print(len(P))
        Q=P

    doc = Document(r'C:\Users\jg2yXRZ\OneDrive\桌面\数独\数独长方形({}宫格）小格.docx'.format(hs))     
#    
    table = doc.tables[0]          # 表0，表2 写标题用的
    # 标题写入3、5单元格  
    for t in range(0,len(bg)):             # 0-5是最下面一行，用来写卡片数字
        pp=int(bg[t][0:2])     # 
        qq=int(bg[t][2:4])
        k=str(Q[t])              # 提取list图案列表里面每个图形  t=索引数字
        print(pp,qq,k)

        # 图案符号的字体、大小参数
        run=table.cell(pp,qq).paragraphs[0].add_run(k)    # 在单元格0,0(第1行第1列)输入第0个图图案
        run.font.name = '黑体'#输入时默认华文彩云字体
        # run.font.size = Pt(46)  #输入字体大小默认30号 换行（一页一份大卡片
        run.font.size = Pt(size) #是否加粗
        # run.font.color.rgb = RGBColor(150,150,150) #数字小，颜色深0-255
        run.font.color.rgb = RGBColor(50,50,50) #数字小，颜色深0-255
        run.bold=True
        # paragraph.paragraph_format.line_spacing = Pt(180) #数字段间距
    
        r = run._element
        r.rPr.rFonts.set(qn('w:eastAsia'), '黑体')#将输入语句中的中文部分字体变为华文行楷
        table.cell(pp,qq).paragraphs[0].alignment = WD_PARAGRAPH_ALIGNMENT.CENTER#居中  

        
    doc.save(r'C:\Users\jg2yXRZ\OneDrive\桌面\数独\零时Word\{}.docx'.format('%02d'%(z+1)))#保存为XX学号的电话号码word     
    time.sleep(2)
    from docx2pdf import convert
    # docx 文件另存为PDF文件
    inputFile = r"C:/Users/jg2yXRZ/OneDrive/桌面/数独/零时Word/{}.docx".format('%02d'%(z+1))# 要转换的文件：已存在
    outputFile = r"C:/Users/jg2yXRZ/OneDrive/桌面/数独/零时Word/{}.pdf".format('%02d'%(z+1))  # 要生成的文件：不存在
    # 先创建 不存在的 文件
    f1 = open(outputFile, 'w')
    f1.close()
    # 再转换往PDF中写入内容
    convert(inputFile, outputFile)
        
    print('----------第4步：把都有PDF合并为一个打印用PDF------------')
        
# 多个PDF合并（CSDN博主「红色小小螃蟹」，https://blog.csdn.net/yangcunbiao/article/details/125248205）
import os
from PyPDF2 import PdfMerger
target_path =  'C:/Users/jg2yXRZ/OneDrive/桌面/数独/零时Word'
pdf_lst = [f for f in os.listdir(target_path) if f.endswith('.pdf')]
pdf_lst = [os.path.join(target_path, filename) for filename in pdf_lst]
pdf_lst.sort()
file_merger = PdfMerger()
for pdf in pdf_lst:
    print(pdf)
    file_merger.append(pdf)

file_merger.write("C:/Users/jg2yXRZ/OneDrive/桌面/数独/（打印合集）05长方形数独宫格21.0 {}宫格{}乘{}等于{}套（{}人{}份）.pdf" .format(hs,db,cb,db*cb,num,num))

file_merger.close()
# doc.Close()

# # print('----------第5步：删除临时文件夹------------')    
import shutil
shutil.rmtree('C:/Users/jg2yXRZ/OneDrive/桌面/数独/零时Word') #递归删除文件夹，即：删除非空文件夹

time.sleep(3)    # 防止转换时报错，预留生成时间





            
            

终端输入：

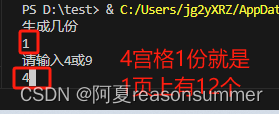
1份4宫格：1页上有12套题

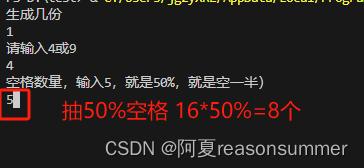
1份9宫格，1页上有6套题

、9宫格有难度，抽30%的空格

4宫格抽取一半空 8空

9宫格抽30%空，24空

结论：

4宫格 2*2格子里包含1-4

9宫格3*3格子里包含1-9

多了一种排除方法，能增加幼儿的计算效率

?