FP16数据格式详解

发布时间：2023年12月23日

1. 浮点格式说明

浮点数的格式通常由三部分组成：符号位(Sign bit)、指数部分(Exponent)和尾数部分(Significand/Fraction)。整个浮点数占用的位数取决于不同的浮点数格式。例如，IEEE 754标准的单精度浮点数（float）有32位，双精度浮点数（double）有64位。参考：Floating-point arithmetic

最终的浮点表示如下，s是significand；p是precision精度(significand中的数字的个数)；b是base，这里base用的是10或者2。
s b p ? 1 × b e \frac{s}{b^{p-1}} \times b^e bp?1s?×be

一个具体的示例如下：
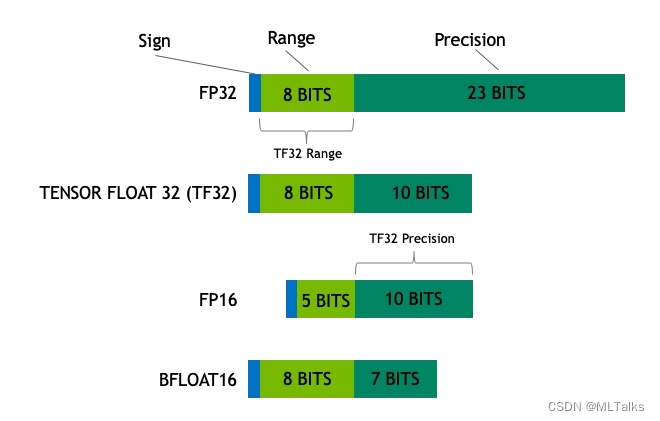
在这里插入图片描述

float32/bfloat16/float16/tf32三种格式的比较:
在这里插入图片描述

2. Normal number

最小的normal number用 b E m i n b^{E_{min}} bEmin? 表示，最大的normal number用
b E m a x ? ( b ? b 1 ? p ) b^{E_{max}} \cdot (b-b^{1-p}) bEmax??(b?b1?p) ，其中 E m i n = ( ? E m a x ) + 1 E_{min} = (-E_{max}) + 1 Emin?=(?Emax?)+1。常用的格式如下：
在这里插入图片描述

3. FP16 Subnormal number

低能数（Subnormal numbers）是指那些比通常能够表示的数字要小的数字。在浮点数的规格化表示中，如果一个数的指数部分全为0且尾数部分不为0，那么这个数就被称为低能数。

对于FP16来说，sign是1位，exponent是5位，fraction是10位。

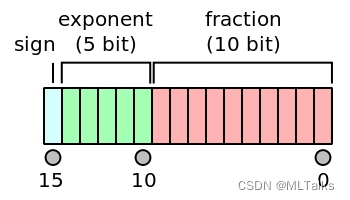
在这里插入图片描述

对于Exponent表示的范围如下：

  • E m i n = 0000 1 2 ? 0111 1 2 = ? 14 E_{min} = 00001_2 - 01111_2 = -14 Emin?=000012??011112?=?14
  • E m a x = 1111 0 2 ? 0111 1 2 = 15 E_{max} = 11110_2 - 01111_2 = 15 Emax?=111102??011112?=15
  • E x p o n e n t ? b i a s = 0111 1 2 = 15 Exponent\ bias = 01111_2 = 15 Exponent?bias=011112?=15

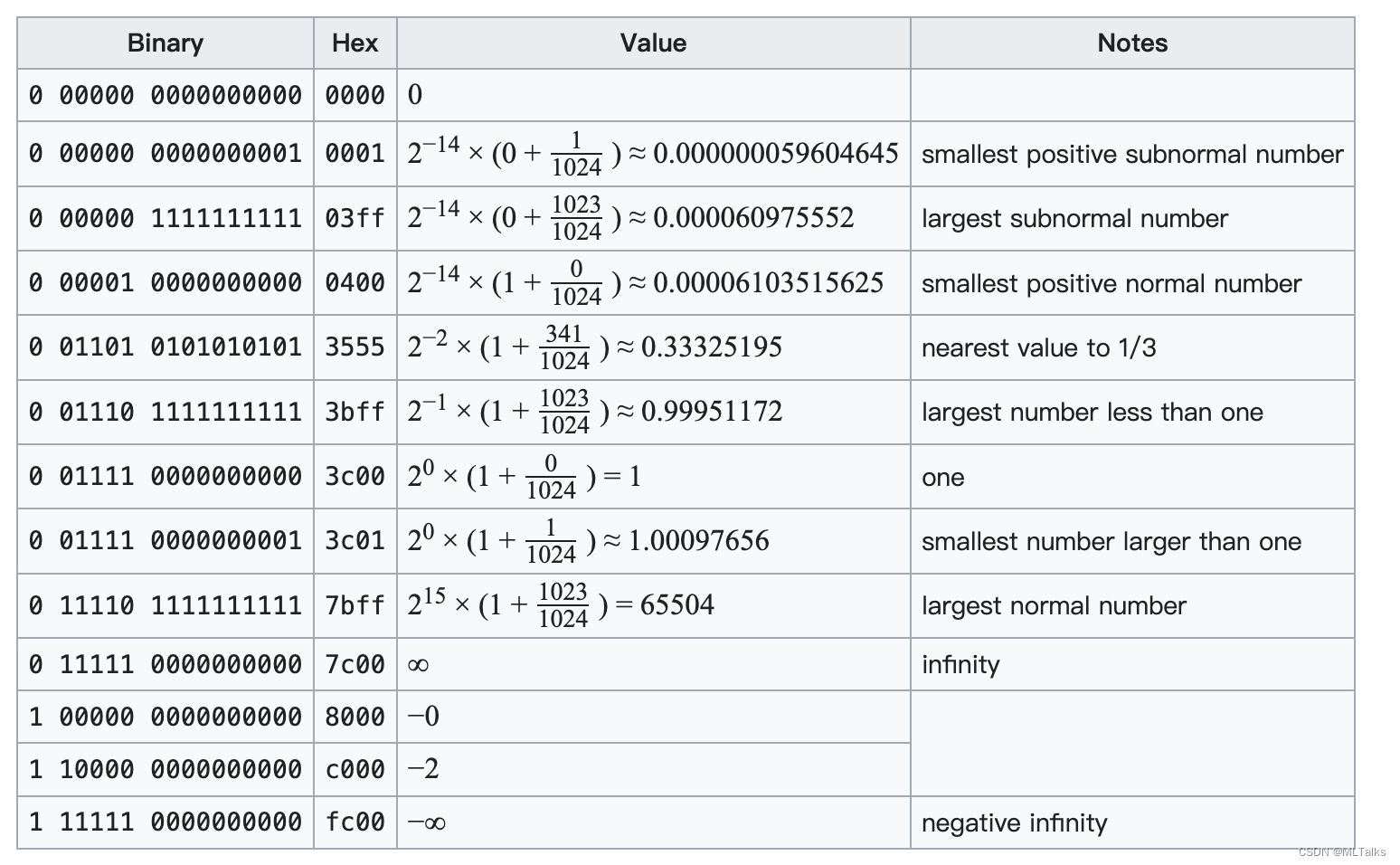
对于FP16表示的范围如下，当Exponent为0且Significand不为0时，对应就是subnormal number的范围，也就是 0.000000059604645 ～ 0.000060975552 0.000000059604645 \sim 0.000060975552 0.000000059604645～0.000060975552。

在这里插入图片描述
在这里插入图片描述

4. 参考

文章来源:https://blog.csdn.net/qinduohao333/article/details/135175163
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章