最优化考试之最速下降法

一、最速下降法

1.前置知识

雅克比矩阵 $?f(x)$的求法

2.问题条件

最速下降法的相关问题中的条件提炼出来如下，如果题目没有误差e，那就要求最后迭代出来的梯度值 $?f(x)$ 接近0或等于0，一般自行选取e。

1. 目标函数 $?f(x)$
2. 初始点 $x^0$
3. 误差 e

3.计算过程

1. 选取初始点$x^0$，$k=0$
2. 计算 $?f$($x^k$) ，若||$?f$($x^k$)||$<=e$，停止迭代，输出结果$x^k$
3. 计算梯度$d=?$$?f$($x^k$)
4. 下一个迭代点 $x^{k+1}$=$x^k$+$t_k$*$d$
5. 设函数$g(t)=f($$x^{k+1}$)，对$g(t)$求导，计算当$g^{\prime }(t)=0$时$t$的值；因此推导出$x^{k+1}$，k=k+1，迭代到第二步

4.例子

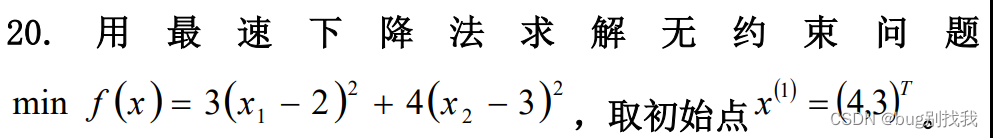
根据3的步骤开始，先求初始点的雅克比矩阵 $?f(x^1)=[6x_1?12,8x_2?24{]}^T$


梯度$d=?$$?f$($x^1$)，下一个迭代点 $x^2=x^1+d?t_1$


设函数$g(t_1)=f(x^2)=3?(?12?t+2{)}^2$


对$g(t_1)$求导，当$g^{\prime }(t_1)=0$时，$t_1=1/6$，代入求得$x^2=[2,3{]}^T$


计算得$?f(x^2)=0$，因此$x^2$为最优解点，最优解为$f(x^2)$