原码，补码的除法

目录

一.原码的除法

（1）恢复余数法

重点看这

（2）不恢复余数法（加减交替法）

重点看这

二. 补码除法运算

重点看这

---

我们已经学习了如何进行原码，补码的乘法：

http://t.csdnimg.cn/GjkIn

现在以同样的思路学习除法运算:

一.原码的除法

对于手算的10进制除法，我们是这样计算的

为什么这样计算呢，我们来看一下：

第一步得到的余数为0.2110,我们需要拼凑上小于等于这个数，且最接近这个数的值，即

0.985*0.2=0.1970，接下来继续以这个规则拼凑

0.985*0.01=0.00985

0.985*0.004=0.00394

最后得到商就是0.214

?那么同理，2进制的手算除法：

计算机如何实现除法：

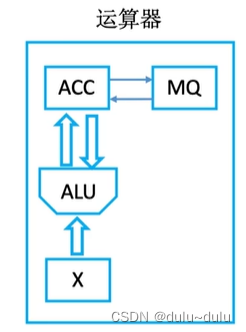
运算器结构如下：

ACC:累加器，用于存放操作数，或运算结果
MQ:乘商寄存器，在乘、除运算时，用于存放操作数或运算结果
X:通用的操作数寄存器，用于存放操作数

ALU:算术逻辑单元，通过内部复杂的电路实现算数运算、逻辑运算

ACC用于存储被除数、余数，MQ用于存储商，X用于存储除数。

（1）恢复余数法

实现方法：上商0/1，得到余数，余数末尾补0

符号位单独处理：符号位=

数值位取绝对值进行除法计算：

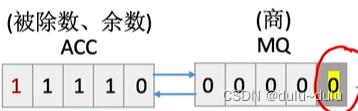
设机器字长为5位(含1位符号位，n=4)，X=0.1011，y=0.1101，采用原码恢复余数法求x/y

|x|=0.1011,|y|=0.1101,[|y|]补=0.1101，[-|y|]补=1.0011

这里注意计算机会默认上商1

?

手算时，每一位商取0/1 是通过判断当前余数和除数的大小确定的：

那么计算机就会将ACC(余数)-通用寄存器(除数)--->ACC

将余数-除数，就是将余数+除数的负值的补码（[-|y|]补），因为计算机中没有减法电路，所有减法都是通过补码的加法等价实现的，这里的加法是通过ALU中的加法电路实现的，不太理解可以先看：

http://t.csdnimg.cn/ZZybo

1.(ACC)+[-|y|]补-->ACC=01011+10011=11110

这里相减的结果是负数，所以说明被除数比除数更小，所以应该上商0，计算机检测到符号位为1，所以将MQ上商0

2.因为商0，而不是商1，所以保存在ACC中的数值是错误的，也就是说

不应该为(ACC)+[-[y]]补-->ACC，而是（ACC）-0-->ACC,为了恢复原来的数，我们再加上[|y|]补，就是

（ACC）+[|y|]补--->ACC

11110+01101=01011

恢复原来的ACC值，并且上商0

3.将ACC与MQ的数统一进行逻辑左移，MQ的最高位会移动到ACC的最低位，原本的ACC最高位被丢弃，低位补0

4.同理，右移后MQ还是会默认上商1：（ACC）-（除数）--->ACC

（ACC）+[-|y|]补--->ACC

? 10110+10011=01001

此时计算机识别当前符号位为正，那么这一步商1是对的

不需要恢复余数，直接进行左移

同理如此重复，可以得到5位商：0.1101

而最终得到的余数需要在0.0111的基础上*(这里的n就是数值位的个数，在这里就是4)

这一步注意，最后一步上商1，若余数为负也就是红色字体为1，那么也需要进行恢复余数并商0

5.最后符号位00=0

重点看这

以上是恢复余数法的所有过程：

1.默认商1，+[-|y|]补

2.余数为负，改为商0，并恢复余数（+[|y|]补），再进行左移

3.余数为正，直接商1，不用恢复余数，直接左移

4.最后的商位数为n+1（数值位+符号位），即上商n+1次，左移n次（最后一次上商不左移）

注：最后一步上商1，若余数为负也就是红色字体为1，那么也需要进行恢复余数并商0

5.异或判断符号位的正负

（2）不恢复余数法（加减交替法）

我们可以观察恢复余数这几部，当发现余数为负时，需要加上[|y|]补恢复余数，在进行左移，减去余数（[-|y|]补）,才能得到下一步的商，根据算式，就是将a--->2a+b的过程：也就是将余数左移一位（2a）+除数的绝对值（b）

所以得到不恢复余数法

重点看这

1.默认商1

2.若余数为负则可直接商0，让余数左移1位再加上|除数|（+[|y|]补）,得到下一个新余数

3.若余数为正，则商1，让余数左移1位再减去|除数| (+[-|y|]补)，得到下一个新余数

4.最后的商位数为n+1（数值位+符号位）

注：加/减n+1次，每次加减确定一位商;左移n次(最后一次加减完不移位)

最终可能还要再多一次加,这需要看余数的正负，下面有讲（所以加/减可能是n+1次，n+2次）

5.异或判断符号位的正负

注：余数的正负性与商相同，若最后一步得到的余数是一个负值，需商0，并且+[|y|]补得到正确的余数

注：这一篇讲的是定点小数的除法运算，被除数一定要小于除数，若被除数大于除数，最后商会为：1.几，而定点小数无法表示大于1的范围，那么机器就是通过第一步得到的商判断的：

第一步被除数-除数，一定为负，商要从默认的1，改为0，若第一步的商不为0，那么就会直接停止除法运算

二. 补码除法运算

补码的除法运算与原码的除法运算中的加减交替法有很多相似

原码中的加减交替法与补码的除法运算的区别：

1.补码除法中，符号位会参与运算

2.被除数/余数，除数都会采用双符号位

3.这里的除数不是原码中的|除数|的补码，而是除数的补码，因为符号位也会参与运算

4.在原码加减交替法中，第一步一定是-|除数|，而在补码的加减交替法中，是根据被除数与除数是否同号来判断+[y]补或+[-y]补

第一步：

被除数和除数同号，则被除数减去除数;

异号则被除数加上除数。

接下来的每一步：
余数和除数同号，商1，余数左移一位减去除数;

余数和除数异号，商0，余数左移一位加上除数。

重复n次

设机器字长为5位(含1位符号位，n=4)，x=+0.1000，y=-0.1011，采用补码加减交替除法求x/y

例如00.1000与11.0101,异号加上除数，得到11.1101,接下来看余数和除数，余数为11.1101，除数为11.0101，同号，商1，余数左移一位并且减除数。如此重复n次（n为数值位的个数）

注意：

在补码中，最后一步是异号的，应该商0，但是在补码加减交替法中，末尾商恒置1，这样做精度误差不超过

而在原码中，若最后一步得到的余数是一个负值，需商0，并且+[|y|]补得到正确的余数

重点看这

1.第一步：被除数和除数同号，则被除数减去除数;异号则被除数加上除数。

接下来的每一步：
余数和除数同号，商1，余数左移一位减去除数;

余数和除数异号，商0，余数左移一位加上除数。

2.最后商位数为n+1(数值位+符号位)，加/减次数n+1，左移次数为n

3.末位恒置1

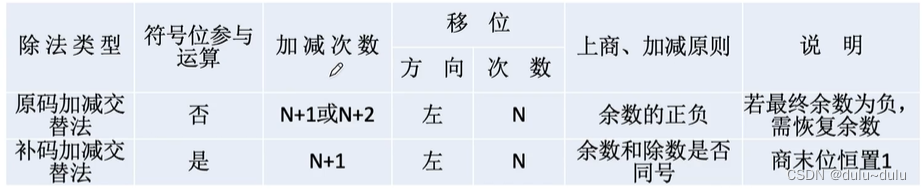
总结：

原码加减交替法与补码加减交替法的区别：