【深度学习】序列生成模型（二）：束搜索

序列生成

??在进行最大似然估计训练后的模型 $p_{\theta }(x|{\mathbf{x}}_{1:(t?1)})$，我们可以使用该模型进行序列生成。生成的过程是按照时间顺序逐步生成序列样本。假设在第 $t$ 步，我们已经生成了前 $t?1$ 步的序列前缀 ${\mathbf{x}}_{1:(t?1)}=x_1,\dots ,x_{t?1}$，我们希望在当前步生成下一个词 $x_t$。生成的过程可以用以下概率分布表示：

$$x_t～p_{\theta }(x|{\mathbf{x}}_{1:(t?1)})$$

其中，${\mathbf{x}}_{1:(t?1)}$ 是已经生成的前缀序列，$x_t$ 是在给定前缀序列的条件下，由模型生成的当前时刻的词。

??这个过程可以迭代进行，直到生成完整的序列样本。在每一步，模型根据已经生成的前缀序列生成当前时刻的词，然后将当前时刻的词添加到前缀序列中，用于生成下一个时刻的词。

生成的序列样本可以用如下方式表示：

$$\hat{\mathbf{x}}={\hat{x}}_1,{\hat{x}}_2,\dots ,{\hat{x}}_T$$

其中，${\hat{x}}_t$ 是在第 $t$ 步生成的词，$\hat{\mathbf{x}}$ 是完整的生成序列。这个过程是根据训练得到的模型对数据分布进行采样，从而生成新的符合训练数据分布的序列。

??自回归的方式可以生成一个无限长度的序列．为了避免这种情况，通常会设置一个特殊的符号?𝐸𝑂𝑆?（End-of-Sequence）来表示序列的结束．在训练时，每个序列样本的结尾都会加上结束符号 $?\text{EOS}?$。训练模型时，这有助于模型学习何时停止生成。在测试时，一旦生成了结束符号 $?\text{EOS}?$，模型就会中止生成过程。

束搜索

理论基础

??在每个时间步，自回归模型贪婪搜索选择当前条件概率分布中具有最高概率的词作为生成的词。具体而言，对于每个时间步 $t$，生成的词 ${\hat{x}}_t$是：

$${\hat{x}}_t=\arg \underset{x\in \mathcal{V}}{\max }{p}_{\theta }(x|{\mathbf{x}}_{1:(t?1)})$$

其中，$\mathcal{V}$ 是词表，${\mathbf{x}}_{1:(t?1)}={\hat{x}}_1,\dots ,{\hat{x}}_{t?1}$ 是前 $t?1$ 步中已经生成的前缀序列。

??这种贪婪搜索策略是一种简单且直观的方法，但它有一个主要的缺点，即可能导致生成的序列不是全局最优的。由于在每个时间步都选择了局部最大概率的词，生成的序列并不保证是整个序列的全局最大概率。这种策略可能导致生成的序列缺乏一致性或流畅性。
??为了改善这种情况，束搜索（Beam Search）是一种常用的启发式方法，特别在序列生成任务中应用广泛。在束搜索中，每个时间步生成多个备选序列，而不仅仅是一个。这样可以在每个时间步维持一个集合，称为束（beam），其中包含多个备选序列。束的大小由超参数 $K$ 决定，通常被称为束大小。

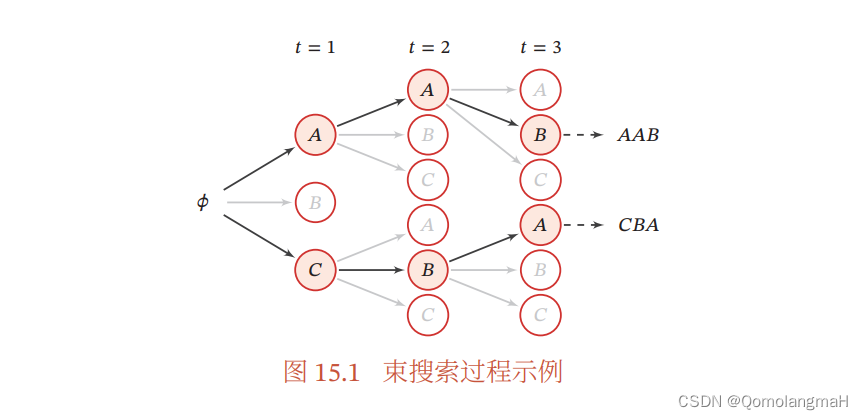
??在每个时间步，算法选择概率最高的 $K$ 个序列作为备选，并将它们作为下一个时间步的输入。这样，算法在整个生成过程中维持了 $K$ 条备选序列，允许更全面地探索可能的序列空间。
??束搜索有助于减少搜索空间，提高搜索的效率。然而，束大小 $K$ 的选择是一个权衡，较小的 $K$ 可能导致搜索空间不够广泛，而较大的 $K$ 则会增加计算开销。因此，束大小的选择通常需要根据具体任务和性能需求进行调整。

算法步骤

1. 初始化： 设置束大小 $K$，初始化一个束（beam）用于存储备选序列。初始时，束中包含一个空序列。

2. 逐步生成： 对于每个时间步 $t$，执行以下步骤：

   a. 对于束中的每个备选序列，生成下一个词的备选集合。计算条件概率 $p_{\theta }(x_t|\text{context})$。

   b. 对于所有的备选序列和它们的备选词，计算在当前时间步的累积概率。

   c. 从所有的备选序列中选择累积概率最高的 $K$个序列作为新的束。

   d. 如果生成了结束符号或达到了最大生成长度，则停止生成。

3. 输出： 选择束中最终累积概率最高的序列作为最终的生成结果。

python实现

def beam_search(model, initial_context, beam_size, max_length):
    # 初始化束，初始时包含一个空序列
    beam = [([], 1.0)]  # 初始序列和初始概率

    # 逐步生成
    for t in range(max_length):
        new_beam = []

        # 对于束中的每个备选序列
        for sequence, score in beam:
            # 生成备选词
            candidates = generate_candidates(model, sequence, initial_context)

            # 计算累积概率
            for candidate in candidates:
                new_sequence = sequence + [candidate]
                new_score = score * calculate_probability(model, new_sequence, initial_context)

                new_beam.append((new_sequence, new_score))

        # 选择累积概率最高的 K 个序列作为新的束
        beam = sorted(new_beam, key=lambda x: x[1], reverse=True)[:beam_size]

        # 判断是否生成了结束符号或达到最大生成长度
        if is_finished(beam):
            break

    # 选择最终累积概率最高的序列作为结果
    best_sequence = max(beam, key=lambda x: x[1])[0]
    return best_sequence