隐马尔可夫模型【维特比算法】

机器学习笔记

机器学习系列笔记，主要参考李航的《机器学习方法》，见参考资料。
第一章 机器学习简介
第二章 感知机
第三章 支持向量机
第四章 朴素贝叶斯分类器
第五章 Logistic回归
第六章 线性回归和岭回归
第七章 多层感知机与反向传播【Python实例】
第八章 主成分分析【PCA降维】
第九章 隐马尔可夫模型

---

---

维特比算法是一种动态规划算法用于寻找最有可能产生观测事件序列的隐含状态序列.

一、维特比算法核心思想

viterbi维特比算法解决的是篱笆型的图的最短路径问题，图的节点按列组织，每列的节点数量可以不一样，每一列的节点只能和相邻列的节点相连，不能跨列相连.

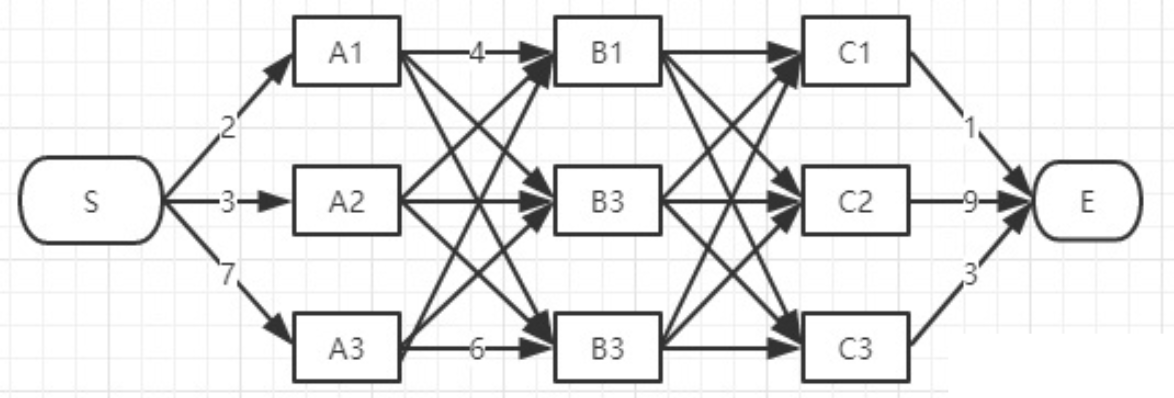
过程非常简单：

1. 为了找出S到E之间的最短路径，我们先从S开始从左到右一列一列地来看。

2. 首先起点是S，从S到A列的路径有三种可能：S-A1、S-A2、S-A3，如下图：

   

S-A1、S-A2、S-A3中的哪一段都有可能是全局最短路径的备选项，我们继续往右看，到了B列。按B列的B1、B2、B3逐个分析：

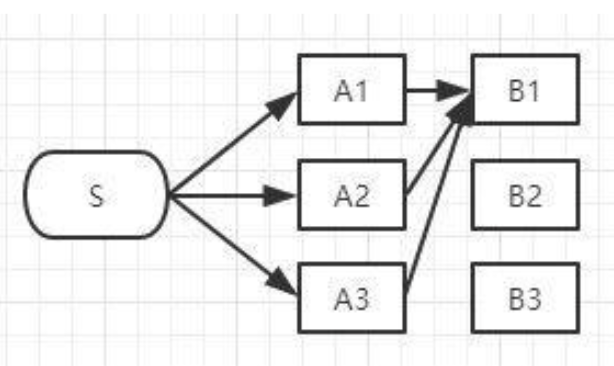
如上图，经过B1的所有路径只有3条：

1. S-A1-B1
2. S-A2-B1
3. S-A3-B1

以上这三条路径，各节点距离加起来对比一下，我们就可以知道其中哪一条是最短的。假设S-A3-B1是最短的，那么我们就知道了经过B1的所有路径当中S-A3-B1是最短的，其它两条路径路径S-A1-B1和S-A2-B1都比S-A3-B1长，绝对不是目标答案，可以删掉了，删掉了不可能是答案的路径，就是viterbi算法（维特比算法）的重点，因为后面我们再也不用考虑这些被删掉的路径了，现在经过B1的所有路径只剩一条路径了，如下图：

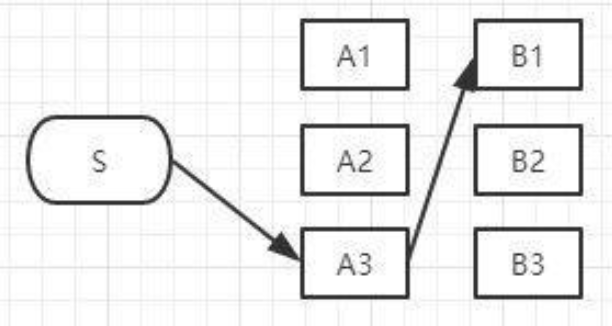
以此类推后面的结点……

二、viterbi算法

viterbi算法的核心主要是：

1. 定义时刻t每个状态$s_i$的路径概率${\delta }_t(i)$.
2. ${\delta }_t(i)$的递推公式.
3. 回溯每个时刻的最优状态.

给定$\lambda =(A,B,\pi )$和长度为$T$的观测序列

0 = { O 1 , O 2 , ? ? , O T } , \mathbf{0}=\{O_1,O_2,\cdots,O_T\}, 0={O1?,O2?,?,OT?},

求与观测序列O最匹配的状态序列

X = { X 1 , X 2 , ? ? , X T } . \mathbf{X}=\{X_1,X_2,\cdots,X_T\}. X={X1?,X2?,?,XT?}.

相当于找到使得$P(X|0,\lambda )$最大的状态序列$X^{?}$, 即

$${\mathbf{X}}^{?}=\underset{\mathbf{X}}{\mathrm{argmax}}P(\mathbf{X}|\mathbf{O},\lambda ),$$所求的最优状态序列$ X^*$也可以定义为
$${\mathbf{X}}^{?}=\underset{\mathbf{X}}{\mathrm{argmax}}P(\mathbf{X},\mathbf{O}|\lambda ).$$考虑时刻 $t\le N$ 状态为 $s_i(1\le i\le N)$ 的所有单个路径
$$(X_1,X_2,?,X_{t?1},X_t=s_i).$$所对应的概率的最大值为（也就是每个时刻每个状态对应观察序列的概率，可以递推）：

$${\delta }_t(i)=\underset{X_1,X_2,...,X_{t?1}}{\max }P(X_t=s_i,X_1,X_2,?,X_{t?1},O_1,O_2,?,O_t),$$
显然对最优路径$X^{?}$而言，
$$P(X^{?},O|\lambda )=\underset{1\le i\le N}{\max }{\delta }_T(i),$$而且
$$X_T^{?}=\arg \underset{s_i,1\le i\le N}{\max }{\delta }_T(i).$$

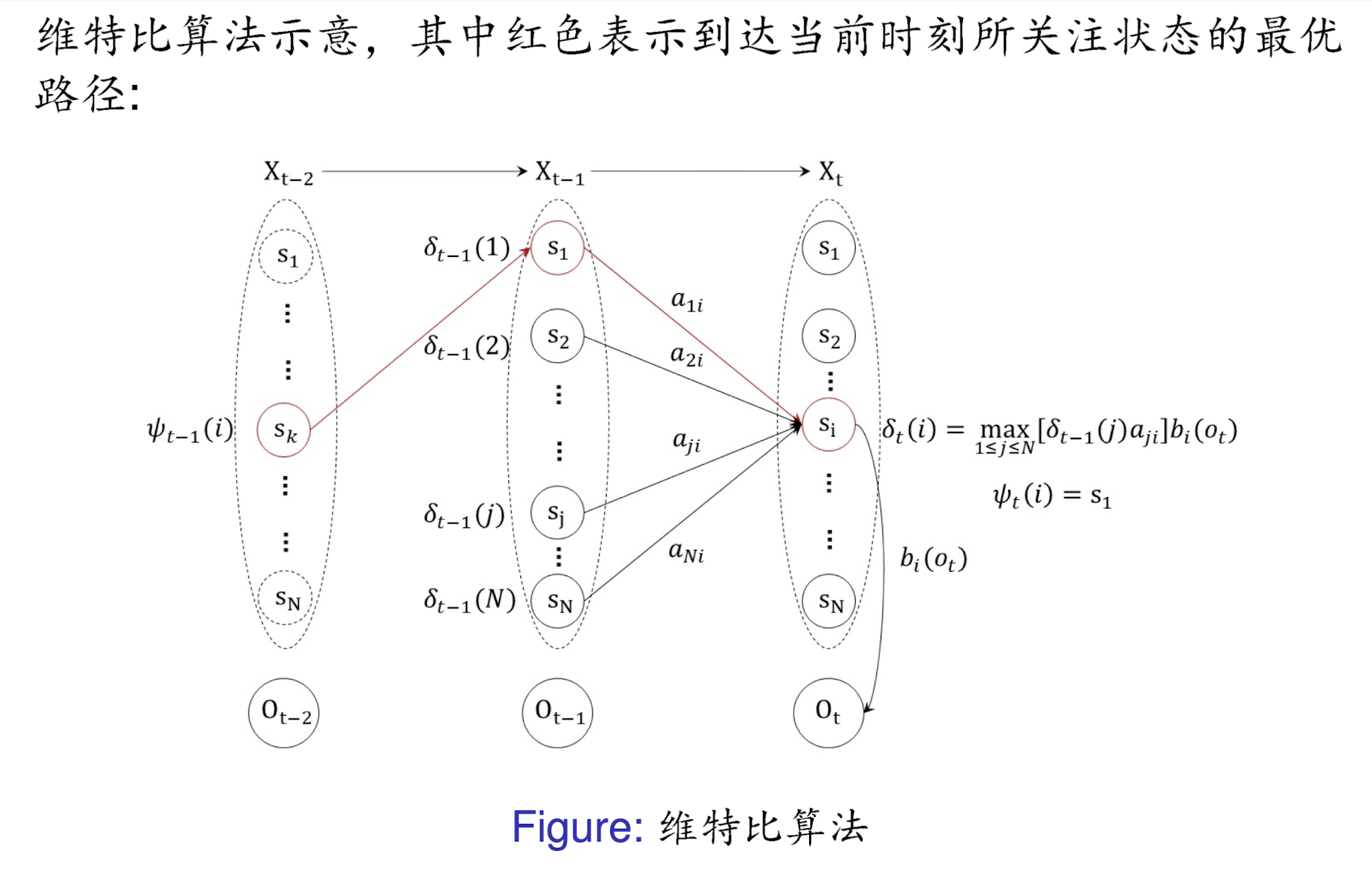
结合第一部分的动态规划思想，路径最大概率${\delta }_t(i)(2\le t\le T)$的递推公式如下：
$${\delta }_t(i)=\underset{1\le j\le N}{\max }[{\delta }_{t?1}(j)a_{ji}]b_i(O_t),i=1,2,?,N.$$由此我们可以递推计算出${\delta }_T(i),i=1,2,?,N.$完整算法框架如下：

参考资料

1. 如何通俗的理解维特比算法
2. 李航. 机器学习方法. 清华大学出版社, 2022.