排序算法之插入排序c++

介绍

插入排序：将数组分成“已排序”和“未排序”两部分。初始时，已排序的部分
包含一个元素，然后从未排序的部分中取出元素，并在已排序的部分中找
到合适的位置进行插入，并保持已排序的部分一直有序。
重复这个过程，直到未排序的部分为空，算法才结束。
最差时间复杂度：O(n^2)
最优时间复杂度：O(n)
平均时间复杂度：O(n^2)
稳定性：稳定

将插入排序比喻为打扑克牌从牌堆中抓牌非常形象和生动。在插入排序中，数组就像是扑克牌的牌堆，而每一次插入操作则像是从牌堆中抓取一张扑克牌，并将其插入到正确的位置。
在插入排序的过程中，初始时，已排序部分只有一张牌（或一个元素），然后从未排序部分（牌堆）中取出一张牌，并在已排序部分找到合适的插入位置插入。这个过程会重复进行，直到未排序部分的牌为空，算法结束。
通过这样的比喻，我们可以更好地理解插入排序的基本思想和工作原理，即通过逐步构建有序序列，最终得到完全有序的数组。

插入排序具体步骤如下：

1. 从第一个元素开始，该元素可以认为已被排序；
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
3. 如果该元素（已排序）大于新元素，将该元素移到下一个位置；
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
5. 将新元素插入到该位置后，重复2~5

算法演示示意图：

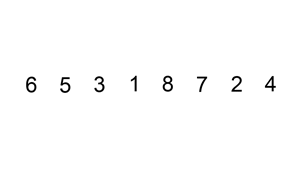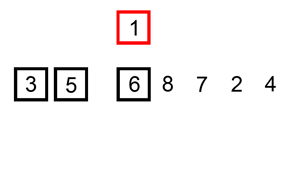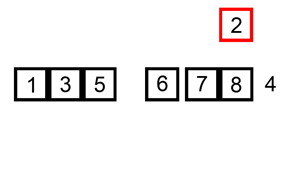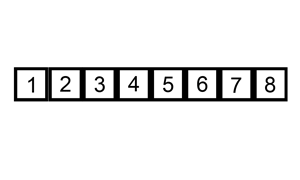
实现代码

#include <iostream>
using namespace std;

void InsertSort(int arr[], int length)
{
	int temp;
	for (int i = 1; i < length; ++i) // 从数组中的第二个元素开始
	{
		temp = arr[i]; // 记录当前的元素
		int j = i - 1;
		while (j >= 0 && temp < arr[j]) // 将当前元素与之前的已经排序好的序列元素进行挨个比较
		{
			arr[j + 1] = arr[j]; // 已经排序好的序列整体向后移动
			--j;
		}
		arr[j + 1] = temp; // 插入当前的元素
	}
}

int main()
{

	int arr[10] = { 9, 2, 8, 2, 3, 2, 4, 10, 34, 5 };
	InsertSort(arr, 10);
	for (int i = 0; i < 10; ++i)
	{
		cout << arr[i] << " ";
	}
	cout << endl;

	return 0;
}

这段代码实现的是插入排序算法，这是一种简单的排序算法。具体解释如下：

首先，代码中定义了一个InsertSort函数，该函数接收一个整数数组arr和它的长度length作为参数。

在InsertSort函数中，使用了两个循环：

1. 外层循环（以i为循环变量）从数组的第二个元素开始，遍历整个数组。
2. 内层循环（以j为循环变量）用于将当前元素arr[i]与前面的已排序好的序列进行比较，并移动元素，为arr[i]腾出位置。

具体过程如下：

• 初始化一个临时变量temp为当前元素arr[i]。
• 使用j从i-1开始向前遍历已排序好的序列。
• 如果temp小于已排序好的序列中的某个元素arr[j]，则将该元素移动到其后面的位置（即arr[j+1] = arr[j]），然后减小j。
• 当找到合适的位置或到达已排序序列的起始位置时，将temp插入到正确的位置（即arr[j+1] = temp）。

主函数main中：

1. 定义了一个包含10个整数的数组arr。
2. 调用InsertSort函数对该数组进行排序。
3. 使用循环输出排序后的数组。

最终，输出结果是：2 2 2 3 4 5 8 9 10 34

这是一个从小到大排序的结果。