代码随想录算法训练营第五十七天|647. 回文子串、516.最长回文子序列、动态规划总结篇

代码随想录 (programmercarl.com)

647. 回文子串

1.dp数组及下标含义

我们在判断字符串S是否是回文，那么如果我们知道 s[1]，s[2]，s[3] 这个子串是回文的，那么只需要比较 s[0]和s[4]这两个元素是否相同，如果相同的话，这个字符串s 就是回文串。

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

2.递推公式

当s[i]与s[j]不相等，dp[i][j]一定是false；

当s[i]与s[j]相等时，有如下三种情况：

• 情况一：下标 i 与? j 相同，同一个字符例如a，当然是回文子串
• 情况二：下标 i 与 j 相差为1，例如aa，也是回文子串
• 情况三：下标：i 与 j 相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看 i 到 j 区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i + 1 与?j - 1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

3.初始化

dp[i][j]初始化为false。

4.遍历顺序

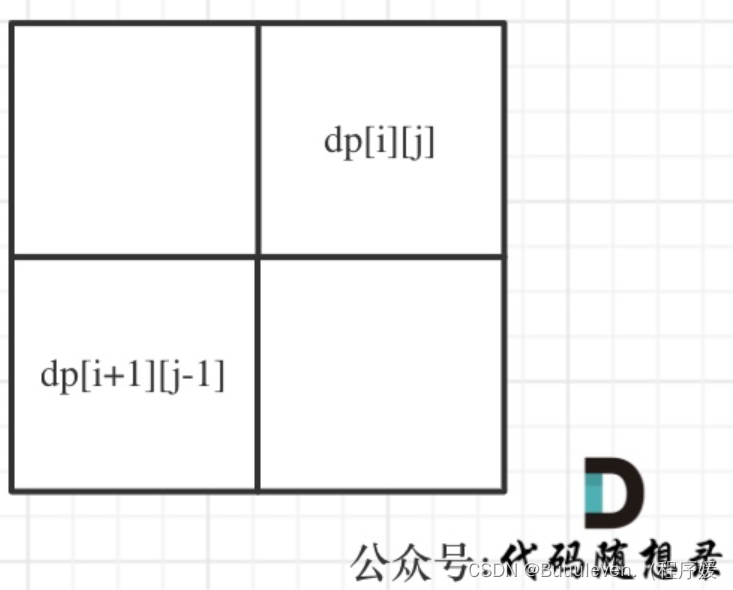
所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

class Solution {
    public int countSubstrings(String s) {
        int len = s.length();
        int res = 0;
        boolean[][] dp = new boolean[len][len];
        for (int i = len - 1; i >= 0; i--) {
            for (int j = i; j < len; j++) {
                if (s.charAt(i) != s.charAt(j)){
                    dp[i][j] = false;
                }else {
                    if (j - i <= 1){
                        res++;
                        dp[i][j] = true;
                    }else {
                        if (dp[i + 1][j - 1]){
                            res++;
                            dp[i][j] = true;
                        }
                    }
                }
            }
        }
        return res;
    }
}

注意：j的遍历开始于i

516.最长回文子序列

LC.617字串==必须连续；LC.516回文子序列===可不连续

1.dp数组及下标含义

dp[i][j]：表示[i, j]范围内的回文子序列长度

2.递推公式

1）当s[i]与s[j]相等时，dp[i][j] =?dp[i + 1][j - 1] + 2

2）当s[i]与s[j]不相等时，

不要s[i]，要s[j]的回文子序列长度为dp[i + 1][j]；

不要s[j]，要s[i]的回文子序列长度为dp[i][j - 1]。

那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

3.初始化

初始化的是递推公式的根基，即i + 1 == j - 1的时候，需要初始化才能够进行递推。

dp[i][i] = 1; 表示同一个字符，其最长回文子序列大小为1

4.遍历顺序

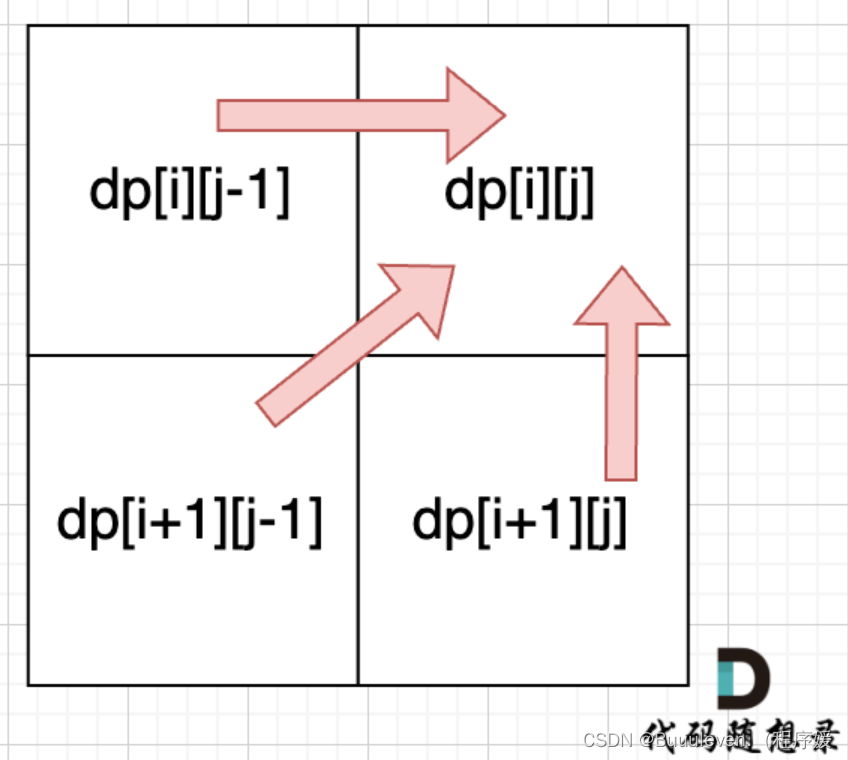
从左往右，从下往上

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len + 1][len + 1];
        for (int i = len - 1; i >= 0; i--) {
            dp[i][i] = 1;
            for (int j = i + 1; j < len; j++) {
            //j = i + 1是因为在i = 0的时候，如果j = i的话，j - 1就越界了
               if (s.charAt(i) == s.charAt(j)){
                   dp[i][j] = dp[i + 1][j - 1] + 2;
               }else{
                   dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][len - 1];
    }
}

动态规划总结篇