列表解析与快速排序

排序是在对文本、数值等数据进行操作时常用的功能，本文介绍两种常用的排序方式，借此学习列表解析，并巩固递归算法。

1 选择排序

说到排序，以数值为例，肯定涉及到值大小的对比，选择排序即通过依次在子集中发现最大或最小值从而实现排序的需求。
首先，我们需要有一个发现最值（以最小值为例）的函数：

def find_min(arr):
	min_val = arr[0]
	min_ind = 0
	for i in range(1, len(arr)):
		if arr[i] < min_val:
			min_val = arr[i]
			min_ind = i
	return min_ind

函数中，我们通过依次对列表的值进行比较，而发现列表中最小的值及其索引。
然后，我们就可以调用find_min()实现选择排序：

def selection_sort(arr):
	arr_sorted = []
	for i in range(len(arr)):
		min_ind = find_min(arr)
		arr_sorted.append(arr.pop(min_ind))
	return arr_sorted

由于每次对比都需要对列表进行操作一次，在排序时又操作一次，因此，算法的时间复杂度是$O_{(n^2)}$，而快速排序是一种更快的排序算法，其平均时间复杂度为$O_{(nlogn)}$！

2 快速排序

不同于选择排序，快速排序采用了D&C的思想，递归的完成排序操作：

def quicksort(arr):
	if len(arr) < 2:
		return arr
	else:
		pivot = arr[0]
		less = []
		greater = []
		for i in arr[1:]:
			if i < pivot:
				less.append(i)
			else:
				greater.append(i)
	return quicksort(less) + [pivot] + quicksort(greater)

在函数中，设置了基准值pivot，通过基准值拆分目标列表，再通过递归不断缩小子集的长度，从而满足基线条件len(arr) < 2。

3 列表解析

通过观察快速排序的代码结构可以发现，创建子集的部分可以使用列表解析的形式来代替，那什么是列表解析呢？列表解析是指根据已有列表，高效创建新列表的方式。先上例子：
在上述代码中创建子集的代码是：

less = []
greater = []
for i in arr[1:]:
	if i < pivot:
		less.append(i)
	else:
		greater.append(i)

实际上可以将这样的代码看成是详细的文字描述：

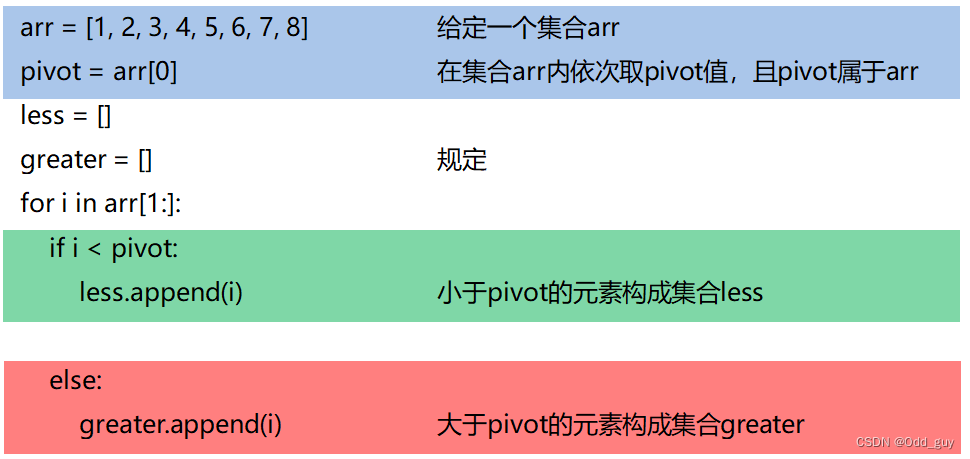
现在我们以数学描述的形式来实现功能：
l e s s = { i ∣ i ∈ a r r , i < p v i o t } less = \lbrace i | i \in arr, i < pviot \rbrace less={i∣i∈arr,i<pviot}

g r e a t e r = { i ∣ i ∈ a r r , i > p v i o t } greater = \lbrace i | i \in arr, i > pviot \rbrace greater={i∣i∈arr,i>pviot}

less = [i for i in arr[1:] if i <= pivot]
greater = [i for i in arr[1:] if i > pivot]

以集合less为例图解：

完整代码：

def quicksort(arr):

    if len(arr) < 2:
        return arr
    else:
    	pivot = arr[0]
    	less = [i for i in arr[1:] if i < pivot]
    	greater = [i for i in arr[1:] if i > pivot]
    	return quicksort(less) + [pivot] + quicksort(greater)

END