时间序列系列02-时间序列分析
1. 时间序列的特点
- 时间依赖性:时间序列数据的不同观测值之间存在时间上的依赖性。过去的数据点可能会对未来的数据产生影响,因此时间序列分析需要考虑这种依赖性。
趋势性:趋势是时间序列数据在长期内表现出的总体变化方向。趋势可以是上升、下降或保持稳定,揭示了数据在长时间范围内的整体趋势变化。 - 季节性:季节性是时间序列数据在短期内(通常是一年内)出现的周期性模式。它可能由特定季节、月份或时间段的影响引起,例如假日销售、季节性天气变化等。
- 周期性:周期性是时间序列数据在长期内出现的重复模式,其周期可能超过一年。周期性通常由经济、社会或其他结构性因素引起。
- 噪声:噪声是随机因素导致的数据波动,使得时间序列数据呈现出一定的不规则性。噪声可能掩盖真实的模式,时间序列分析需要区分噪声和真实信号。
- 季节性变动:季节性变动是数据在短期内出现的周期性波动,其周期通常为一年。这种波动可能与自然季节、假日、特定事件等有关。
- 自相关性:自相关性指的是时间序列数据中不同时间点之间的相关性。自相关性分析有助于了解数据点与其过去时间点之间的关系,为建立预测模型提供信息。
- 平稳性:时间序列的平稳性意味着其统计性质在时间内保持不变。平稳性对于许多时间序列模型的假设是重要的,可以通过差分等方法来实现。
时序分析的任务: 时间序列分析的目标是从数据中提取出这些特点和模式,进行未来趋势预测、异常检测、决策制定等。
2.时间序列的相关检验
2.1 平稳性检验
1. 平稳性检验的意义
- 可靠的统计性质: 平稳性确保了时间序列在不同时间点上的统计性质(如均值、方差、自相关性等)是稳定的。这使得我们可以更可靠地计算和解释这些统计性质,而不受时间的影响。
- 时间序列分析方法的有效性: 许多时间序列分析方法,例如自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)等,要求时间序列是平稳的。只有在序列平稳的情况下,我们才能应用这些方法来进行模型的建立和预测。
- 模型假设的满足: 在许多统计模型中,平稳性是一个重要的假设。如果时间序列不是平稳的,那么模型的估计和预测可能会受到非平稳性的影响,导致结果不可靠。
- 避免伪回归: 在非平稳的时间序列中,即使没有真正的关系,自变量和因变量之间可能出现看似显著的关联。这被称为伪回归(spurious regression)问题。平稳性有助于避免这种问题,确保我们在建模时关注真实的关系。
- 更好的预测性能: 平稳性有助于提高时间序列模型的预测性能。通过保持统计性质的稳定性,模型更容易捕捉和预测未来的趋势和模式。
2. 平稳性检验的方法
进行平稳性检验的方法之一是使用单位根检验(Unit Root Test)。谓单位根,是指一种非平稳性的表现形式,如果一个序列存在单位根,那么这个序列就被认为是非平稳的。
常用的单位根检验包括 Augmented Dickey-Fuller 测试(ADF 测试)和 Kwiatkowski-Phillips-Schmidt-Shin 测试(KPSS 测试)。
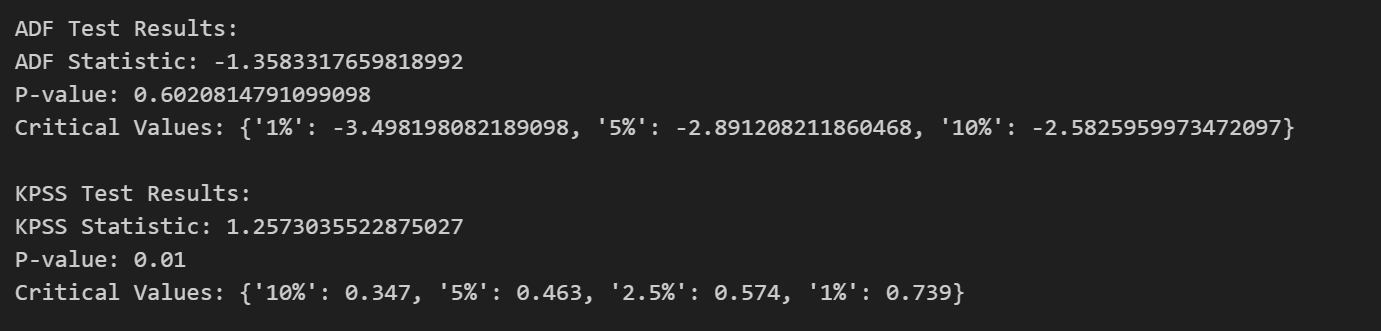
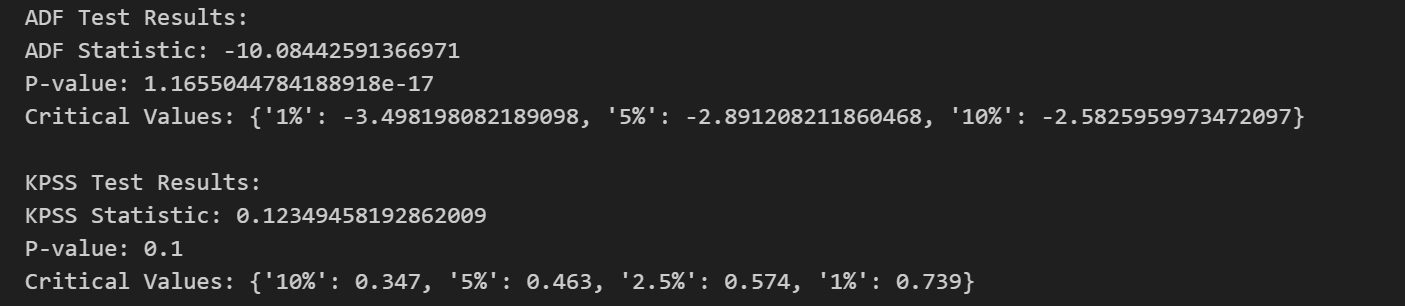
对于 ADF 测试,零假设是该时间序列具有单位根,即是非平稳的。而备择假设则是该时间序列不具有单位根,也就是平稳的。若p-value小于显著性水平(0.05),则可以认为拒绝原假设,数据不存在单位根,序列平稳;若大于或等于显著性水平(0.05),则不能显著拒绝原假设,需要进行下一步判断。
如果得到的显著性检验统计量小于三个置信度(10%,5%,1%),则对应有(90%,95,99%)的把握来拒绝原假设,即为平稳序列。
对于 KPSS 测试,在KPSS检验中,零假设是该时间序列是平稳的,而备择假设则是该时间序列存在单位根,即是非平稳的。如果 p-value 大于显著性水平,我们可以接受原假设,即序列是平稳的。
def adf_checkout(time_series):
"""
进行ADF检验,判断时间序列是否平稳。
参数:
time_series (np.array): 要检验的时间序列数据。
返回:
tuple: 包含ADF统计量、p值、临界值等信息的元组。
"""
result_adf = adfuller(time_series)
print("ADF Test Results:")
print(f"ADF Statistic: {result_adf[0]}")
print(f"P-value: {result_adf[1]}")
print(f"Critical Values: {result_adf[4]}")
return result_adf
def kpss_checkout(time_series, regression='c', nlags='auto', store=False):
"""
进行KPSS平稳性检验,判断时间序列是否平稳。
参数:
time_series (np.array): 要检验的时间序列数据。
regression (str): 回归类型,可选'c'、'ct'、'ctt'。默认为'c'。
nlags (int or str): 滞后阶数。默认为'auto'。
store (bool): 是否存储结果。默认为False。
返回:
tuple: 包含KPSS统计量、p值、临界值等信息的元组。
"""
result_kpss = kpss(time_series, regression=regression, nlags=nlags, store=store)
print("\nKPSS Test Results:")
print(f"KPSS Statistic: {result_kpss[0]}")
print(f"P-value: {result_kpss[1]}")
print(f"Critical Values: {result_kpss[3]}")
return result_kpss
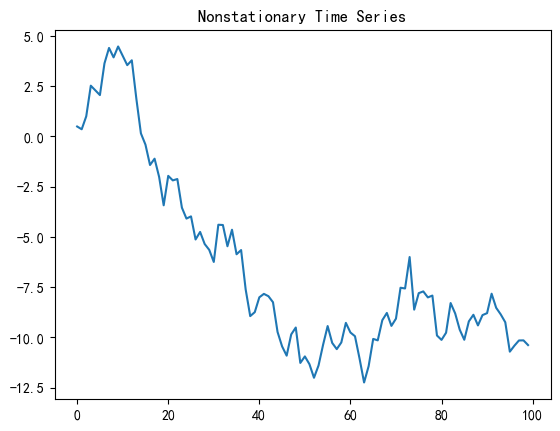
非平稳测试:
# 生成一个非平稳时间序列的示例数据
np.random.seed(42)
nonstationary_data = np.cumsum(np.random.normal(size=100))
# 绘制非平稳时间序列的时序图
plt.plot(nonstationary_data)
plt.title("Nonstationary Time Series")
plt.show()
平稳测试
3. 转化为平稳序列的方法
将非平稳时间序列转化为平稳时间序列的常见方法包括差分(Differencing)和对数转换。这些方法有助于消除序列中的趋势和季节性,从而使其更平稳。
以下是两种常用的转化方法:
差分(Differencing): 通过计算序列的差分,即当前时刻的观测值与上一个时刻的观测值之差,可以移除趋势和季节性。一般情况下,一阶差分(first-order differencing)足以使序列平稳,但在某些情况下可能需要使用更高阶的差分。
import numpy as np
import matplotlib.pyplot as plt
# 生成一个有趋势和季节性的非平稳时间序列
np.random.seed(42)
t = np.arange(100)
nonstationary_series = 0.5 * t + 10 * np.sin(0.1 * t) + np.random.normal(0, 1, 100)
# 绘制非平稳时间序列的时序图
plt.plot(nonstationary_series)
plt.title("Nonstationary Time Series")
plt.show()
# 一阶差分,移除趋势和季节性
stationary_series = np.diff(nonstationary_series, n=1)
# 绘制平稳时间序列的时序图
plt.plot(stationary_series)
plt.title("Stationary Time Series")
plt.show()
对数转换: 如果时间序列的波动性与均值相关,可以考虑对数转换。对数转换有助于缩小大值和小值之间的差距,使序列更加稳定。
import numpy as np
import matplotlib.pyplot as plt
# 生成一个有趋势和季节性的非平稳时间序列
np.random.seed(42)
t = np.arange(100)
nonstationary_series = 0.5 * t + 10 * np.sin(0.1 * t) + np.random.normal(0, 1, 100)
# 绘制非平稳时间序列的时序图
plt.plot(nonstationary_series)
plt.title("Nonstationary Time Series")
plt.show()
# 对数转换
log_transformed_series = np.log1p(nonstationary_series)
# 绘制平稳时间序列的时序图
plt.plot(log_transformed_series)
plt.title("Log-Transformed Time Series")
plt.show()
2.2 白噪声检验
1. 白噪声检验的意义
时间序列的白噪声检验主要是为了确定时间序列数据是否具有随机性,也就是说,数据的未来时间序列的白噪声检验主要是为了确定时间序列数据是否具有随机性,即数据的未来值是否可以被其过去值和现在值所预测。
如果一个序列是平稳的,那么我们需要判断数据是否为白噪声。一个纯白噪声的时间序列没有研究的意义,因为从一个纯随机的东西中我们无法找出任何有价值的规律。
白噪声检验除了可以用于在预测前判断平稳序列是否随机外,还能用于检验残差是否为白噪声,从而判断模型拟合的是否足够好,是否还存在有价值的信息待提取。如果残差为白噪声,说明模型拟合得很好,残差部分为无法捕捉的纯随机数据;如果残差非白噪声,则说明模型可能存在问题,需要进行调整或优化。
2.白噪声检验的方法
纯随机性检验原理:Barlett定理
如果一个时间序列是纯随机的,得到一个观察期数为n的观察序列,那么该序列的延迟非零期的样本自相关系数将近似服从均值为0,方差为序列观察期数倒数的正态分布。根据Barlett定理,我们可以构造检验统计量来检查序列的纯随机性。

Box E PG和Pierce D A(1970)提出了Q检验统计量,如式(5)所示,其中,n为时间长度,m为滞后阶参数(Q检验统计量的参数)。Q检验统计量渐近服从自由度为m-k的卡方分布,k为估计参数的个数。严格地讲,Q统计只有在大样本下才渐进服从卡方分布,因此,Ljung G M和E P Box G(1978)对Q进行了修改,提出了适合小样本的Q统计量,如式(6)所示,该统计量也渐进服从自由度为m-k的卡方分布。
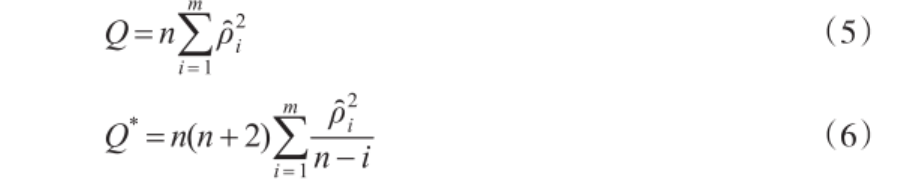
Box-Pierce检验:即Q检验,其只有在大样本下才渐进服从卡方分布,如式(5)所示
Ljung-Box(LB)检验:即修正Q检验,如式(6)所示。是一种用于检验时间序列数据是否存在自相关性的统计方法。它是基于时间序列的自相关函数(ACF)的平方和进行的检验,用于判断序列是否表现出显著的自相关。其基本思想是检验序列在不同滞后阶数上的自相关是否显著地不等于零。其零假设是序列在所有滞后阶数上都不存在自相关,即序列是白噪声。如果 p 值小于显著性水平(例如 0.05),则可以拒绝零假设,认为序列在给定滞后阶数上存在自相关,不是白噪声。否则,不能拒绝零假设,序列可能表现为白噪声。
自相关性图和偏自相关性图检验:
自相关性是指时间序列中一个时刻的观测值与该序列中过去某个时刻的观测值之间的关系。具体而言,自相关函数(Autocorrelation Function,ACF)衡量了一个时刻与不同滞后阶数的过去时刻之间的相关性。ACF通常在滞后阶数(lag)为不同值时计算,形成自相关图。
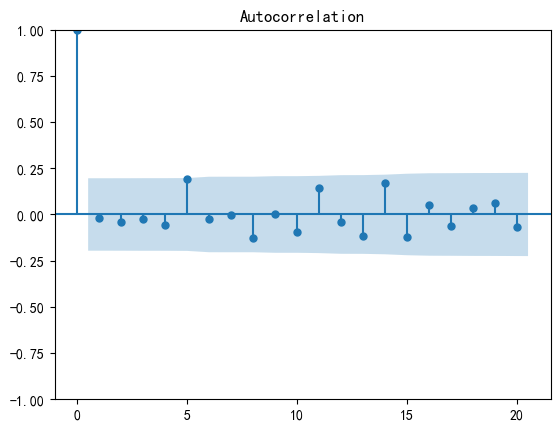
如果生成的随机数是真正的白噪声,那么自相关函数应该只在零延迟处有一个峰值,其他地方的值都接近零。
偏自相关性是一种控制其他滞后值的影响,专注于描述一个时刻与特定滞后阶数的过去时刻之间的关系。偏自相关函数(Partial Autocorrelation Function,PACF)在滞后阶数为不同值时计算,形成偏自相关图。
如果生成的随机数是真正的白噪声,那么偏自相关函数(Partial Autocorrelation Function,PACF)在滞后阶数超过其截尾滞后阶数后应该快速趋近于零
ps:
自相关系数的解释:
自相关系数是衡量时间序列中一个变量与其自身在不同时间点上的相关性的指标。
具体来说,自相关系数衡量的是时间序列中当前观测值与先前观测值之间的相关性。自相关系数的计算通常使用公式:这里,lag表示滞后阶数,Covariance表示协方差,Var表示方差。
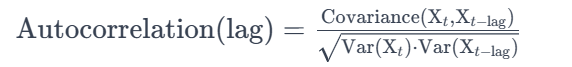
滞后阶数的解释:滞后阶数表示在时间序列分析中考虑的滞后期数,即在计算自相关系数时,要考虑多少期的观测值。例如0阶滞后项代表没有位移的原始时序,一阶滞后项代表时序数据向左移动一位,多阶滞后项以此类推。在时间序列分析中,如果我们设定了最大滞后阶数为5,那么就表示我们将考虑当前时刻的因变量和过去5个时刻的自变量纳入模型中。
代码:
#加载包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# import pmdarima as pm
from statsmodels.tsa.stattools import adfuller,kpss
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
#中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
import warnings
warnings.filterwarnings('ignore')
def lb_checkout(time_series, lags=[2,4,6,8,10]):
"""
实施Ljung-Box检验/ Box-Pierce和自相关函数(ACF)/偏自相关(PACF)来检验
参数:
time_series (np.array): 要检验的时间序列数据。为一列数据
lags (int): 要考虑的滞后数。
boxpierce: 默认为 True。如果为 True,则同时开启 Box-Pierce 检验,否则只进行 Ljung-Box 检验。
return_df: 默认为 True。如果为 True,则返回一个包含 Ljung-Box 检验统计量和相关统计量的 Pandas DataFrame。
返回:
lb_stat: QLB检验统计量(Ljung-Box检验)
lb_pvalue: QLB检验统计量下对应的P值(Ljung-Box检验) p 值大于显著性水平(0.05)则认为为白噪声
bp_stat: QBP检验统计量,boxpierce为False时不返回(Box-Pierce检验)
bp_pvalue: QBP检验统计量下对应的P值,boxpierce为False时不返回(Box-Pierce检验) p 值大于显著性水平(0.05)则认为为白噪声
"""
res = acorr_ljungbox(time_series, lags=lags,boxpierce=True,return_df=True)
# 如果生成的随机数是真正的白噪声,那么自相关函数应该只在零延迟处有一个峰值,其他地方的值都接近零。
plot_acf(time_series) #自相关分析图
# 如果生成的随机数是真正的白噪声,那么偏自相关函数(PACF)在滞后阶数超过其截尾滞后阶数后应该快速趋近于零
plot_pacf(time_series)#偏相关分析图
plt.show()
return res
# 生成随机时间序列
np.random.seed(42)
random_series = np.random.normal(size=100)
# 绘制时间序列图
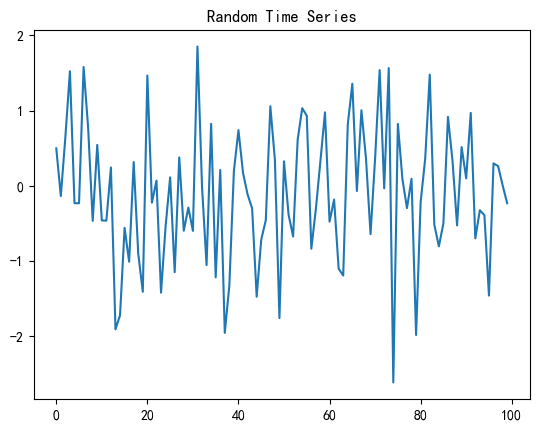
plt.plot(random_series)
plt.title("Random Time Series")
plt.show()
res = lb_checkout(random_series)
res
结果: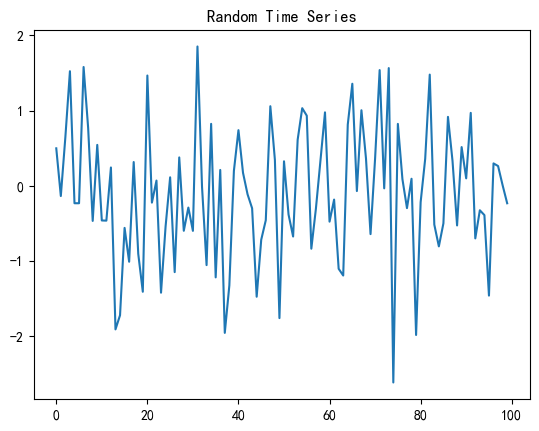
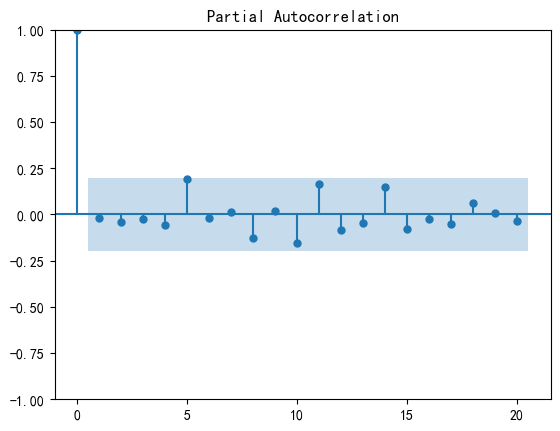
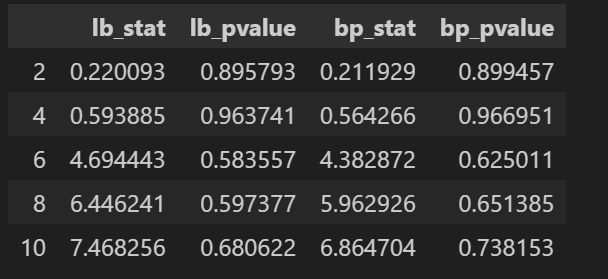
3.时间序列分解
时间序列分解是时间序列分析中的一个重要步骤,用于识别和分离时间序列数据中的不同成分,如趋势、季节性和周期性波动等。这些成分可以独立地对原始时间序列进行建模和分析,以更深入地理解数据的内在结构和动态。
一个时间通常由长期趋势,季节变动,循环波动,不规则波动几部分组成
长期趋势指现象在较长时期内持续发展变化的一种趋向或状态。
季节波动时间序列在特定时间段内出现的周期性波动
循环波动指在某段时间内,不具严格规则的周期性连续变动
不规则波动指由于众多偶然因素对时间序列造成的影响
分解模型又分为加法模型和乘法模型。加法指的是时间序列的组成是相互独立的,四个成分都有相同的量纲。乘法模型输出部分和趋势项有相同的量纲,季节项和循环项是比例数,不规则变动项为独立随机变量序列,服从正态分布。
Y
[
t
]
Y[t]
Y[t]是时间序列在时刻 t 的观测值
T
[
t
]
T[t]
T[t]是趋势组成部分
S
[
t
]
S[t]
S[t]是季节性组成部分
C
[
t
]
C[t]
C[t]是循环项
I
[
t
]
I[t]
I[t]是不规则变动项(残差项)

时间序列分解的方法可以根据具体的数据特性和分析目的而有所不同,但以下是一种常见的时间序列分解方法:
经典分解法:将时间序列分解为趋势、季节性和残差三个部分,有加法模型和乘法模型两种
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
# 生成一个有趋势和季节性的时间序列
np.random.seed(42)
t = np.arange(100)
time_series = 0.5 * t + 10 * np.sin(0.1 * t) + np.random.normal(0, 1, 100)
# 经典分解 multiplicative/additive
result = seasonal_decompose(time_series, model='additive', period=12)
# 绘制分解结果
plt.figure(figsize=(12, 8))
plt.subplot(4, 1, 1)
plt.plot(time_series, label='Original')
plt.legend()
plt.subplot(4, 1, 2)
plt.plot(result.trend, label='Trend')
plt.legend()
plt.subplot(4, 1, 3)
plt.plot(result.seasonal, label='Seasonal')
plt.legend()
plt.subplot(4, 1, 4)
plt.plot(result.resid, label='Residuals')
plt.legend()
plt.tight_layout()
plt.show()
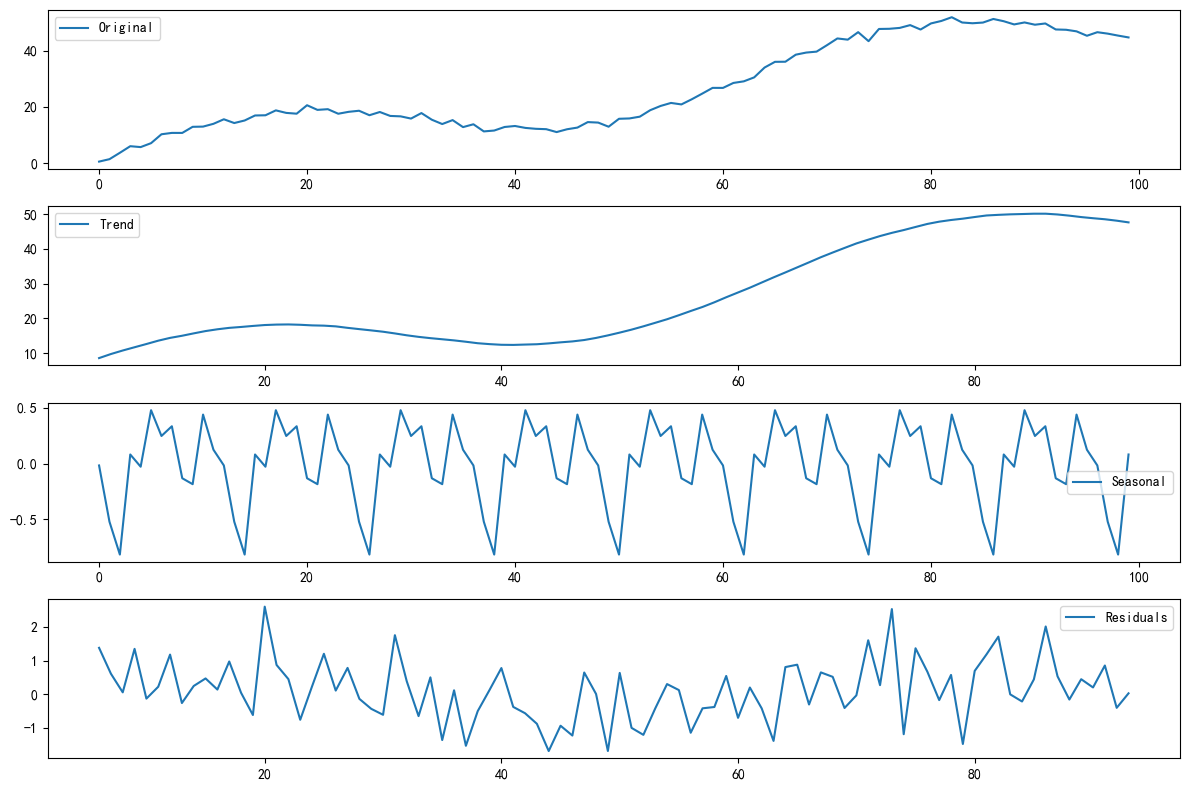
STL 分解法:STL(Seasonal and Trend decomposition using Loess)是一种更灵活的分解方法,通过局部加权散点平滑法(Loess smoothing)对时间序列进行分解。STL 分解法还允许处理非固定周期的季节性,对异常值的影响较小。( statsmodels.tsa.seasonal.STL Season-Trend decomposition using LOESS.)
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import STL
# 生成一个有趋势和季节性的时间序列
np.random.seed(42)
t = np.arange(100)
time_series = 0.5 * t + 10 * np.sin(0.1 * t) + np.random.normal(0, 1, 100)
# STL 分解
result = STL(time_series, period=12).fit()
# 绘制分解结果
plt.figure(figsize=(12, 8))
plt.subplot(4, 1, 1)
plt.plot(time_series, label='Original')
plt.legend()
plt.subplot(4, 1, 2)
plt.plot(result.trend, label='Trend')
plt.legend()
plt.subplot(4, 1, 3)
plt.plot(result.seasonal, label='Seasonal')
plt.legend()
plt.subplot(4, 1, 4)
plt.plot(result.resid, label='Residuals')
plt.legend()
plt.tight_layout()
plt.show()
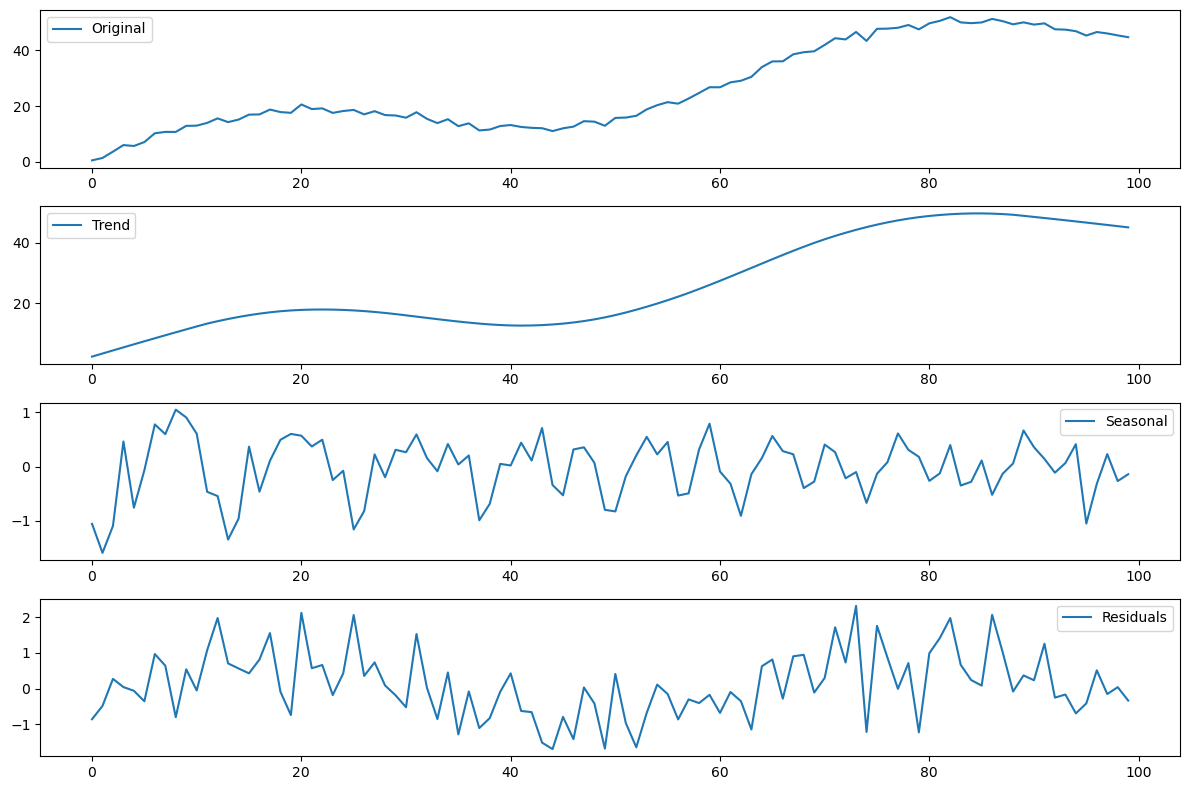
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- HW01—SY系列单点测厚仪 应用于轧钢橡胶、金属、塑料…
- locust快速入门--使用locust-plugins保存类似jmeter的csv数据
- pg,postgres 数据库设置自增主键,自定义设置自增主键的值
- DSP定时器0笔记
- 基于遗传算法的药品配送,遗传算法原理
- C语言小游戏——3、寻找大公约和小公倍的多种求法
- 基于STM32的水质在线监测系统(论文+源码)
- 项目实操四-性能测试过程实时监控分析
- drf之路由
- 内网环境安装python3版本,以及一些python的包遇到的坑