【K12】练习使用Python数学函数解物理中的电功率变化的问题

练习使用Python数学函数解物理问题

在现代教育中，电路与电子学是理工科学生必修的基础课程。通过学习和实践电路知识，学生们能够深入理解电流、电压、电阻等基本概念，以及它们在电子设备中的应用。本文旨在通过一个具体案例，探讨在电路分析过程中如何应用数学知识，特别是方程组的建立与求解，来得到电路中各元件的参数值，并进一步计算电路的电功率变化范围。希望读者通过本文，不仅能够加深对电路知识的理解，还能体会到数学在解决实际问题中的重要作用，激发对数学和电路学的兴趣。

注意：
1、未知变量的表示方法，sy.symbols()直接赋值给字符本身。
2、电压方程sp.Eq(),使用2次列出二个方程，然后用函数sp.solve()，解方程，参数1方程存储变量，参数2，未知数，参数3：词典为True,得到保存未知数结果的字典。
3、从词典中提取结果，这样完成求未知量过程。

import sympy as sp

# 定义变量
R1, U = sp.symbols('R1 U')

# 已知条件
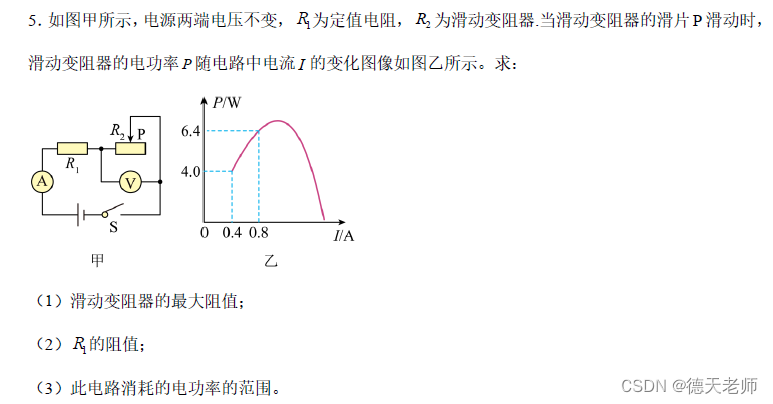
I1 = 0.4  # 第一次测量的电流
P1 = 4.0  # 第一次测量时滑动变阻器的功率
R2_1 = P1 / I1 ** 2  # 第一次测量时滑动变阻器的电阻（也是R2的最大值）

I2 = 0.8  # 第二次测量的电流
P2 = 6.4  # 第二次测量时滑动变阻器的功率
R2_2 = P2 / I2 ** 2  # 第二次测量时滑动变阻器的电阻

# 建立方程组
# 第一次测量时的电压方程
equation1 = sp.Eq(U, I1 * (R1 + R2_1))
# 第二次测量时的电压方程
equation2 = sp.Eq(U, I2 * (R1 + R2_2))

# 使用solve解方程组
solutions = sp.solve((equation1, equation2), (R1, U), dict=True)
R1_value = solutions[0][R1]
U_value = solutions[0][U]

# 计算整个电路电功率的变化范围
# 当滑动变阻器接入电路中的电阻为0时，电路中的电流最大，电功率最大
I_max = U_value / R1_value
P_max = U_value * I_max

# 当滑动变阻器接入电路中的电阻最大时（R2_1），电路中的电流最小
# 但此时的总功率不是最小的，因为滑动变阻器上也有功率消耗
# 我们已经知道此时滑动变阻器上的功率是P1
# 所以需要计算R1上的功率，然后相加得到总功率
I_min = I1  # 因为这是第一次测量时的电流
P_R1_min = I_min ** 2 * R1_value
P_min = P1 + P_R1_min
#用round有时达不到保留小数位效果，用格式化方法反而更有效果。
print(f"计算结果为：R1 = {R1_value:.1f}Ω, U = {U_value:.1f}V")
print(f"滑动变阻器R2的最大值为：{round(R2_1,1)}Ω")  # 添加这一行来显示R2的最大值
print(f"整个电路电功率的变化范围为：{round(P_min,1)}W 到 {round(P_max,1)}W")

通过本文的探讨，我们了解了如何利用数学方法分析电路，并得到电路中各元件的参数以及电功率的变化范围。电路作为电子设备的基础，其重要性不言而喻。掌握电路分析的方法不仅有助于学生理解电子设备的工作原理，还能为他们在将来设计和开发新的电子设备时提供宝贵的理论支持和实践经验。

数学在电路分析中的应用，再次证明了数学作为一门基础学科的普遍性和实用性。无论是在学术研究中，还是在工程实践中，数学都发挥着不可替代的作用。希望通过本文的学习，读者们能够更加重视数学的学习与应用，将其作为分析和解决问题的有力工具。同时，也期待读者们在实际操作中不断探索和创新，将理论知识与实践相结合，为电子技术的发展贡献自己的力量。