【数据结构】快速排序(4种方式实现)
前言:前面我们学习了几种相对比较简单的排序,今天我们要一起学习的是快速排序,我们将通过四种方式来模拟实现快排。
💖 博主CSDN主页:卫卫卫的个人主页 💞
👉 专栏分类:数据结构 👈
💯代码仓库:卫卫周大胖的学习日记💫
💪关注博主和博主一起学习!一起努力!
C语言算法-快速排序
什么是快速排序
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
快速排序之hoare版
hoare思想
1.首先我们选定一个基准值,通常是数组中的第一个元素。
2. 定义俩个指针,一个left一个right分别在数组的最左边和最右边。
3. 我们让右指针先走,如果比我们定义的基准值小就停下来。
4. 右指针走完我们在让左指针走,如果比我们定义的基准值小也停下来。
5. 在俩个指针都停下来的时候把它们的值进行交换,以此反复循环直到俩个指针相遇,我们把基准值和它们的值进行交换。
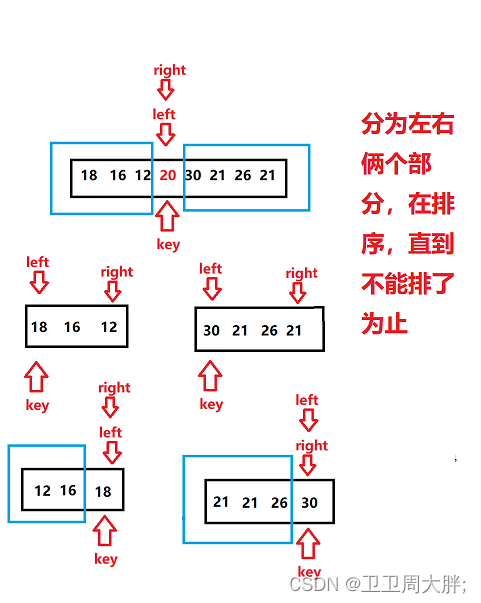
6. 最终这一趟下来我们会得到如下图一样的数据,基准值左边的都比基准值小,右边的都比基准值大。
7. 我们把这一趟走完后在重新分为左右俩个部分的数据,在用此方法以此往复即可实现一个有序数组。

代码思路:刚刚我们用那个思想可以实现一次的排序过程,可是排完一次那剩下的怎么排呢?我们可以把这个问题拆成许多个小问题(如下图所示),因此我们可以采用递归的思想来实现它。
代码实现:
void QuickSort1(int* a,int begin, int end)//快速排序 -- hoare
{
int right = end;
int left = begin;
int key = begin;
if (begin >= end)
{
return;
}
while (left < right)
{
while (a[right] >= a[key] && right >left)
{
right--;
}
while (a[left] <= a[key] && right > left)
{
left++;
}
Swap(&a[right], &a[left]);
}
Swap(&a[key], &a[left]);
key = left;
QuickSort1(a, begin, left - 1);//左边
QuickSort1(a, key+1, end);//右边
}
测试函数:
void Test_QuickSort1()
{
int a[] = { 20,16,30,18,12,21,26,21 };
QuickSort1(a, 0, sizeof(a) / sizeof(a[0]) - 1);
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
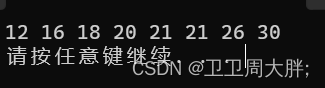
运行结果:
快速排序之挖坑法
挖坑思想:
- 首先我们和前面的hoare法一样,我们选定一个基准值,通常是数组中的第一个元素。
- 我们定义一个坑位(hole)放在基准值的位置的下面。
- 我们同理定义俩个指针left和right一个在数组的最左边一个在最右边。
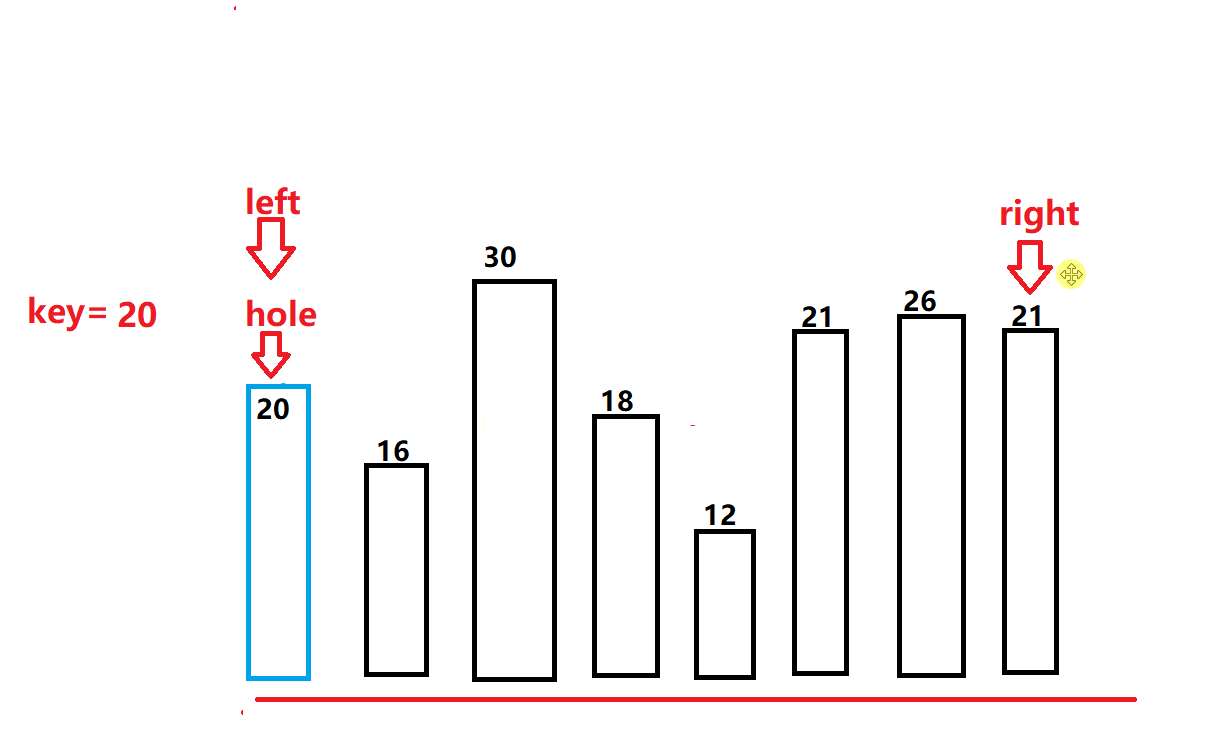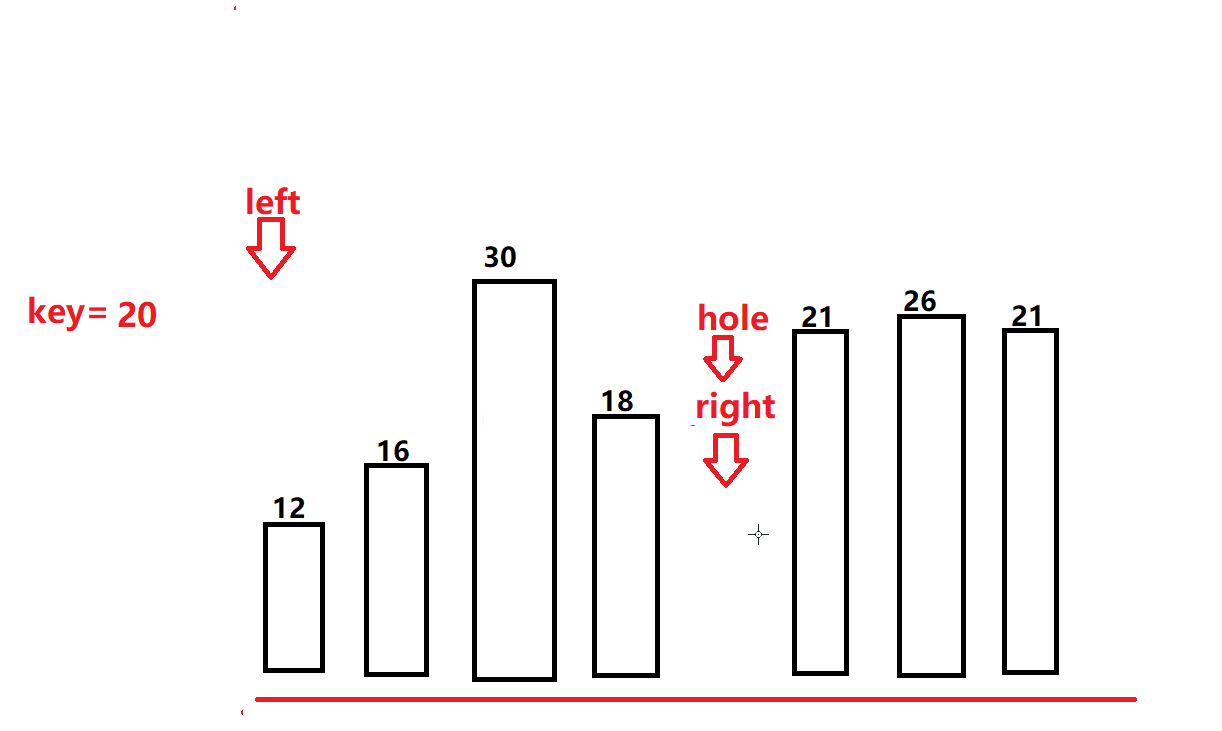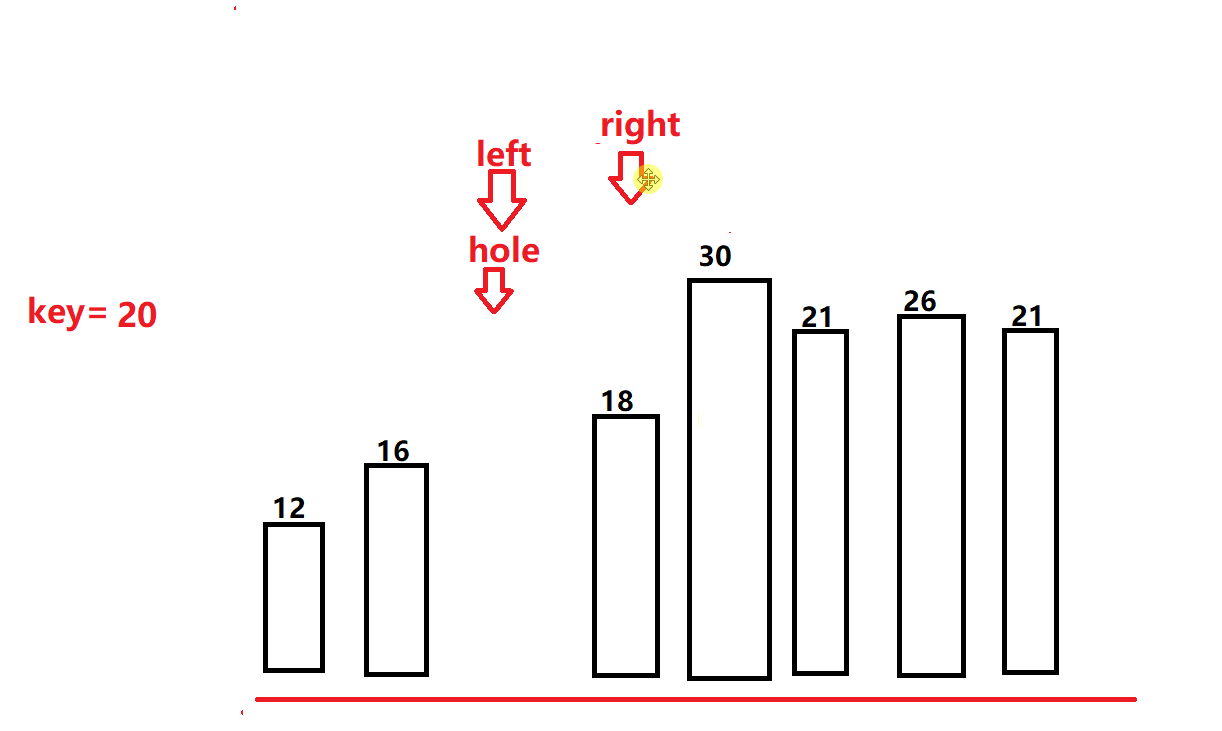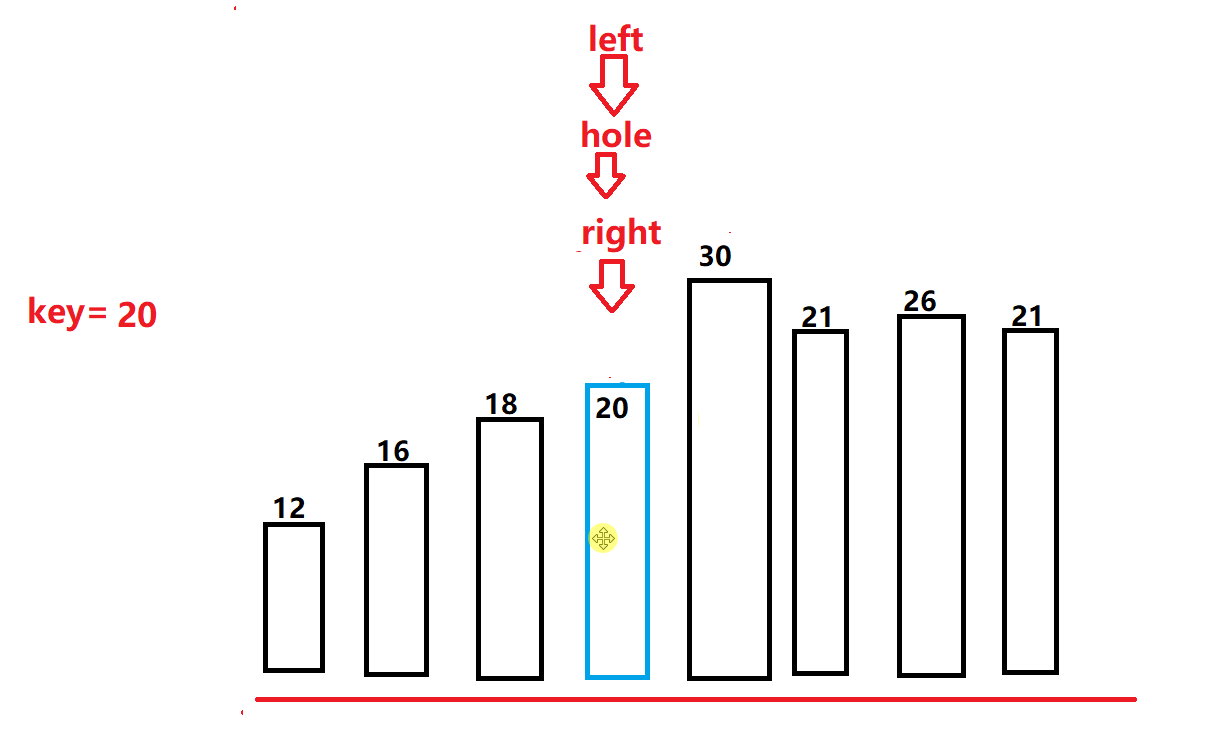
- 不同的是,我们right指针找到比基准值小的值的时候,就直接和坑位所对应的值交换,并把right此时的位置置为hole。
- 同理left也行动开始找值补坑,找到比基准值大的值将其放入坑位,置为新的坑。
- 以此往复,当left和right相遇的时候,在将基准值放入坑位。此时我们也会发现和hoare一样的排序结果,右边的值都比基准小,左边的都比其大。(如下图所示)
代码实现:
void PartSort2(int* a,int begin ,int end)//快速排序 -- 挖坑法
{
int right = end;
int left = begin;
int hole = left;
int key = a[begin];
if (begin >= end)
{
return;
}
while(left < right)
{
while(a[right] >= key && right > left)
{
right--;
}
a[hole] = a[right];
hole = right;
while (a[left] <= key && right > left)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
QuickSort1(a, begin, hole - 1);//左边
QuickSort1(a, hole + 1, end);//右边
}
测试函数:
void Test_PartSort2()
{
int a[] = { 20,16,30,18,12,21,26,21 };
PartSort2(a, 0, sizeof(a) / sizeof(a[0]) - 1);
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
运行结果:

快速排序之前后指针法
双指针思想
双指针法相较于前面俩种方式,是目前主流的一种写法,这里我们依然来看看单趟的走法。
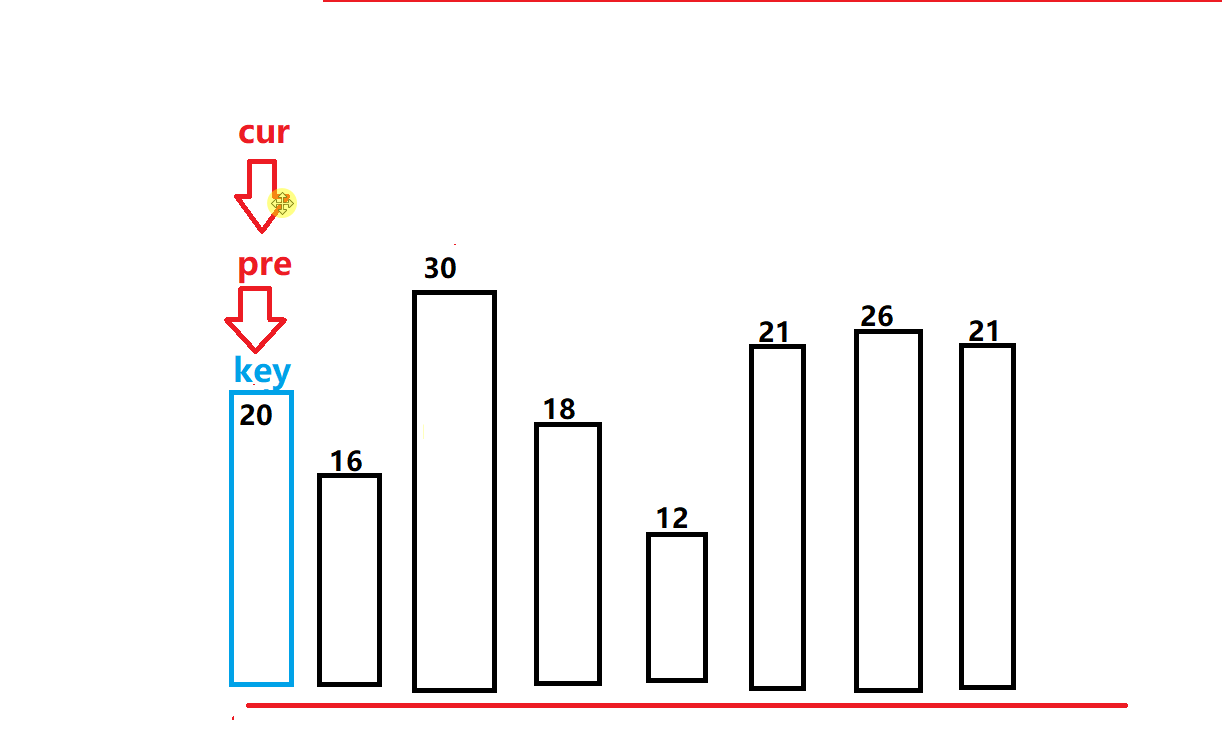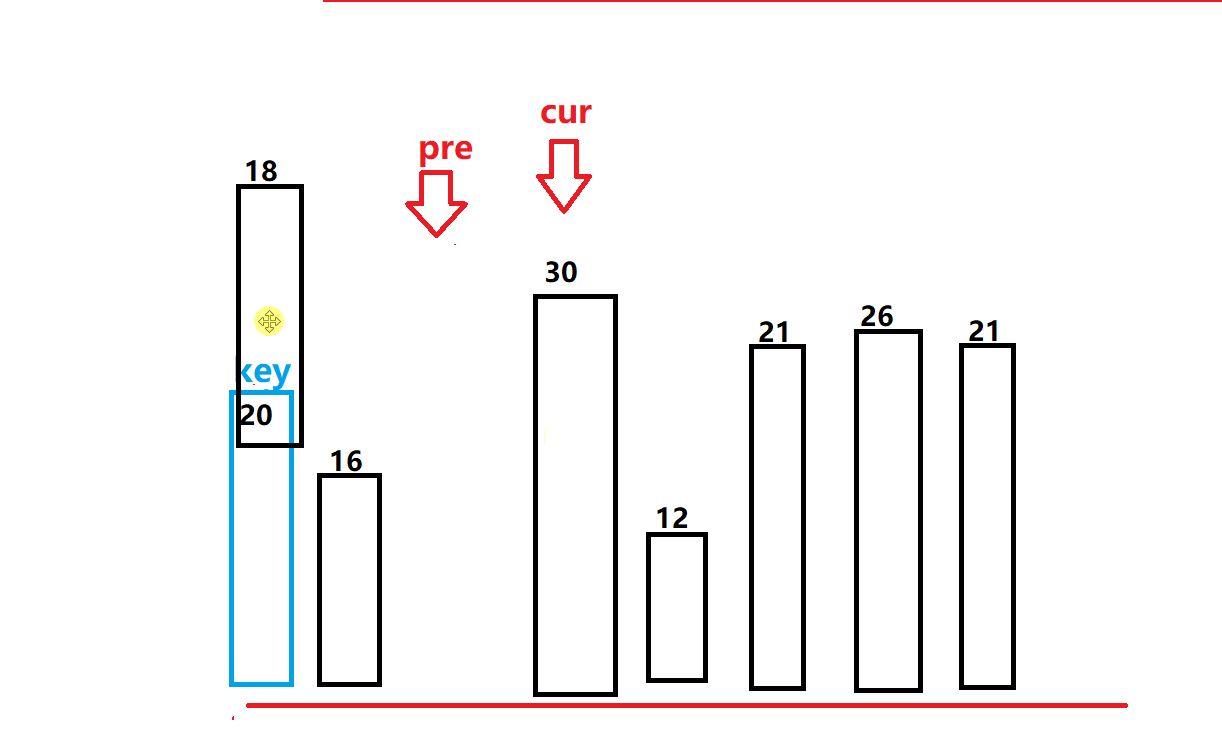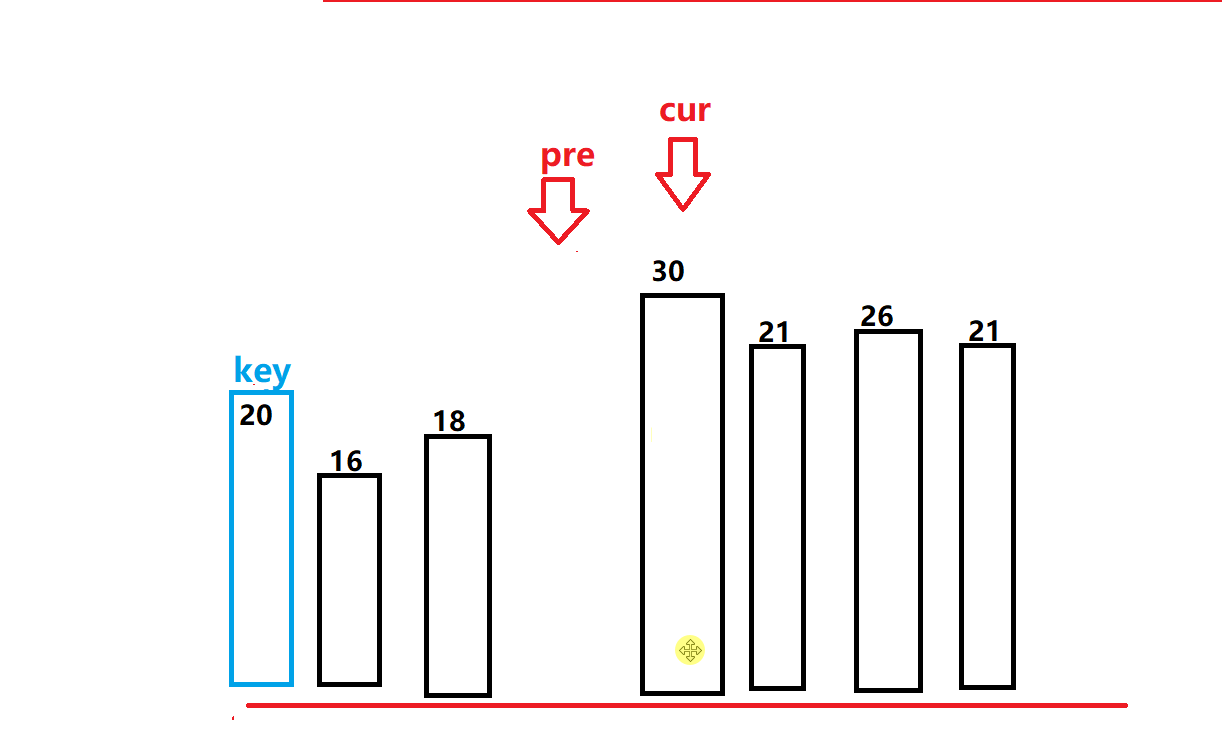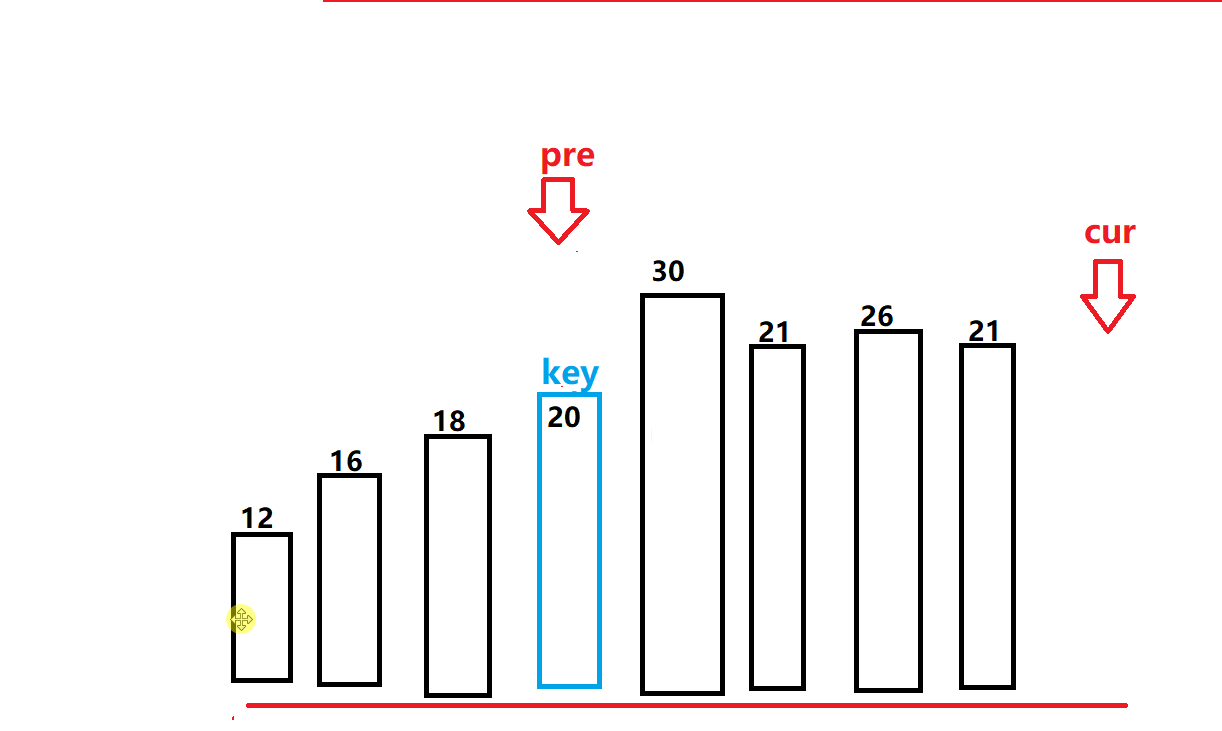
- 这里我们依然和前面的俩种法一样,我们选定一个基准值,通常是数组中的第一个元素。
- 定义一个pre和一个cur指针,同理,我们让cur指针先走,如果遇到比基准值小的值我们就停下来,然后让pre指针往前走一步,我们再对其进行交换。
- 注意,在交换的时候我们pre指针和cur指针不能是处于同一位置。
- 当pre指针和cur指针相遇的时候,我们就让此次循环终止,在将基准值和此时的pre值进行交换即可(cur值可能已经走出边界所以不能是cur)。此时我们也会发现和hoare和挖坑法一样的排序结果,右边的值都比基准小,左边的都比其大。(如下图所示)
代码实现:
void PartSort3(int* a, int begin, int end)//双指针法 //cur遇到比key大的++cur cur遇到比key小的值,++prev,交换pre和cur的位置的值, ++cur
{
int pre = begin;
int cur = pre+1;
int key = begin;
while (cur <= end && pre <= end)
{
if(a[cur] < a[key] && cur != ++pre)
{
Swap(&a[cur], &a[pre]);
}
++cur;
}
Swap(&a[key], &a[pre]);
QuickSort1(a, begin, pre - 1);//左边
QuickSort1(a, pre + 1, end);//右边
}
函数测试
void Test_PartSort3()
{
int a[] = { 20,16,30,18,12,21,26,21 };
PartSort3(a, 0, sizeof(a) / sizeof(a[0]) - 1);
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
运行结果:

快速排序之非递归排序
非递归思想
因为递归是在函数栈帧是在栈上开辟的,十分容易出现溢出的现象,为了防止这个问题,我们有一种非栈帧的方式来实现排序,就是通过非递归的方式来实现,即用栈(前面所学的数据结构中的栈)来模拟实现。
- 入栈一定得保证先左再右即我们先进去的是左区间,再进去的是右区间。
- 将每次入栈的数据进行单趟排序。
- 再将剩余的部分划分成 [left,key-1] 与 [key+1,right]
- 循环此操作直到栈中的数据全部为空即可(如果不理解可以看下图)。
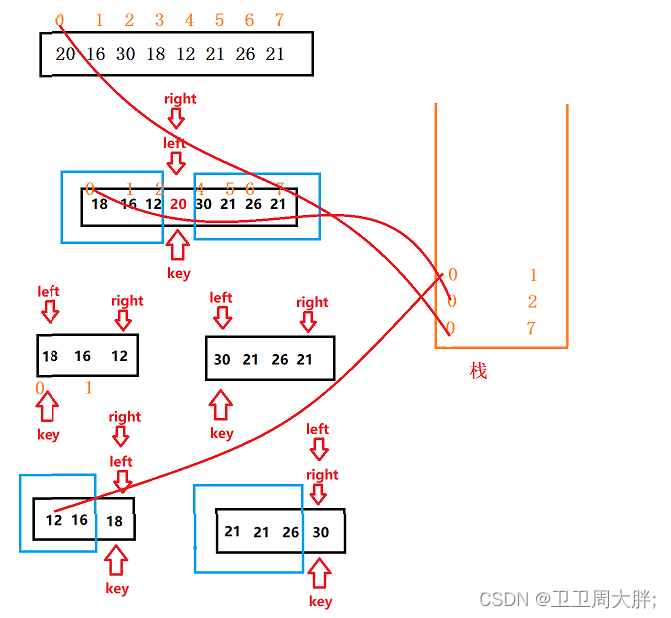
代码实现:
int PartSort4(int* a, int begin, int end)//双指针法 //cur遇到比key大的++cur cur遇到比key小的值,++prev,交换pre和cur的位置的值, ++cur
{
int pre = begin;
int cur = pre + 1;
int key = begin;
while (cur <= end && pre <= end)
{
if (a[cur] < a[key] && cur != ++pre)
{
Swap(&a[cur], &a[pre]);
}
++cur;
}
Swap(&a[key], &a[pre]);
key = pre;
return key;
}
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, left);
STPush(&st, right);
while (!STEmpty(&st))
{
int end = STTop(&st);//右边
STPop(&st);
int begin = STTop(&st);//左边
STPop(&st);
int key = PartSort4(a, begin,end);//第一趟排序的区间
//[left, key - 1] key [key + 1, right];
if (key + 1 < end)//判断此时是左区间还是右区间
{
STPush(&st, key + 1);
STPush(&st, end);
}
if (begin < key - 1)
{
STPush(&st, begin);
STPush(&st, key - 1);
}
}
STDestroy(&st);
}
测试函数:
void Test_QuickSortNonR()
{
int a[] = { 20,16,30,18,12,21,26,21 };
QuickSortNonR(a,0, sizeof(a) / sizeof(a[0]) - 1);
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
运行结果:

结语:今天的内容就到这里吧,谢谢各位的观看,如果有讲的不好的地方也请各位多多指出,作者每一条评论都会读的,谢谢各位。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
