牛客周赛 Round 28 F
发布时间:2024年01月15日
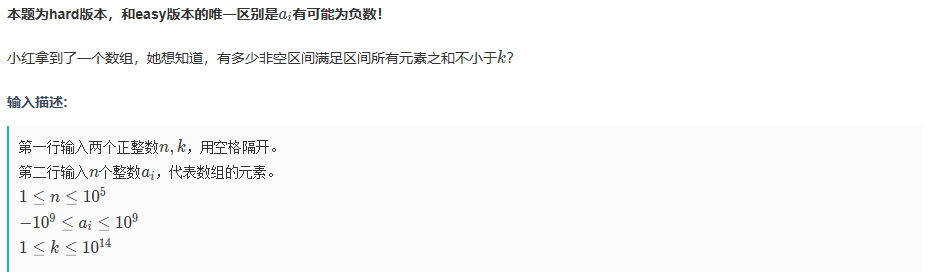
以后需要使用map,set进行二分,并且需要知道二分位置的信息时,不妨考虑使用树状数组进行维护
因为简单版本保证了每个数都为正整数,所以前缀和保证了一定的递增的,即有序的,那么考虑固定左端点,去枚举右端点,用二分去找到第一个合法的位置,那么从该位置到数组结尾,一直为合法的,或者使用双指针进行维护也行。
基于简单版本的思想,那么对于区间问题,我们同样考虑去固定一个端点,去维护另外一个,又因为
a
i
a_i
ai?可能为负数,所以前缀和不保证单调性了,不能采用二分的方法,此时想到,我们对于每个右端点,我去计算其对应左端点的贡献即可,那么我每遍历一个位置,我就把该位置的前缀和放入一个数据结构中,该结构必须保证有序,这样对于当前位置,我一样可以使用二分该数据结构,然后找到合法的位置,一开始在考虑map,set之类,但这种虽说支持二分,但是不支持下标访问,即我无法知道对于合法位置之前有多少个数,这时候就该树状数组登场了,因为这题数据范围过大,所以需要先进行离散化,树状数组中插入该前缀和所在的位置即可,树状数组的查询同样是log级别,至此此题结束。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+ 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<int, 4> ar;
int mod = 998244353;
const int maxv = 4e6 + 5;
// #define endl "\n"
struct MIT
{
ll tr[N];
int lowbit(int x) {
return x & (-x);
}
void add(int u, int v) {
for (int i = u; i < N; i += lowbit(i)) {
tr[i] += v;
}
}
ll query(int x) {
ll res = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
res += tr[i];
}
return res;
}
};
MIT tr;
void solve()
{
ll n,k;
cin>>n>>k;
vector<ll> a(n+5),s(n+5);
for(int i=1;i<=n;i++) cin>>a[i];
vector<ll> p;
for(int i=1;i<=n;i++) {
s[i]=s[i-1]+a[i];
p.push_back(s[i]);
p.push_back(s[i]-k);
}
p.push_back(0);
ll ans=0;
sort(p.begin(),p.end());
p.erase(unique(p.begin(),p.end()),p.end());
int t=lower_bound(p.begin(),p.end(),0)-p.begin()+1;
tr.add(t,1);
for(int i=1;i<=n;i++){
ll tar=s[i];
int t=lower_bound(p.begin(),p.end(),tar)-p.begin()+1;
tr.add(t,1);
int pos=lower_bound(p.begin(),p.end(),s[i]-k)-p.begin()+1;
// cout<<tr.query(pos)<<endl;
ans+=tr.query(pos);
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t=1;
// cin>>t;
while(t--){
solve();
}
system("pause");
return 0;
}
文章来源:https://blog.csdn.net/Unlimited_ci/article/details/135608762
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章