5.3 WARPS AND SIMD HARDWARE

我们现在把注意力转向线程执行中可能限制性能的方面。回想一下，启动CUDA内核会生成一个线程网格，该网格被组织为两级层次结构。在顶层，网格由一维、二维或三维块阵列组成。在底层，每个块依次由一维、二维或三维线程阵列组成。在第3章，可扩展并行执行中，我们看到块可以以任何相对的顺序执行，这允许跨不同设备的透明可扩展性。然而，我们没有过多说明每个块内线程的执行时间。

从概念上讲，人们应该假设块中的线程可以相互之间以任何顺序执行。在具有相位的算法中，每当我们想确保所有线程在开始下一阶段之前都已完成执行的通用阶段时，就应该使用屏障同步。我们在tile矩阵乘法内核中看到了这样一个例子。执行内核的正确性不应取决于某些线程将相互同步执行的事实。话虽如此，我们还想指出，由于各种硬件成本考虑，当前的CUDA设备实际上捆绑了多个线程进行执行。这种实现策略导致某些类型的内核代码构建的性能限制。对于应用程序开发人员来说，将这些类型的构造更改为其他性能更好的等效形式是有利的。

正如我们在第3章“可扩展并行执行”中所讨论的，每个线程块都被划分为warps。warp的执行由SIMD硬件实现（请参阅“warp和SIMD硬件”边栏）。这种实施技术有助于降低硬件制造成本，降低运行时操作电力成本，并实现内存访问的合并。在可预见的未来，我们预计warp分区仍将作为一种流行的实现技术。然而，warp的大小很容易因实现而异。到目前为止，所有CUDA设备都使用了类似的warp配置，每个warp由32个线程组成。

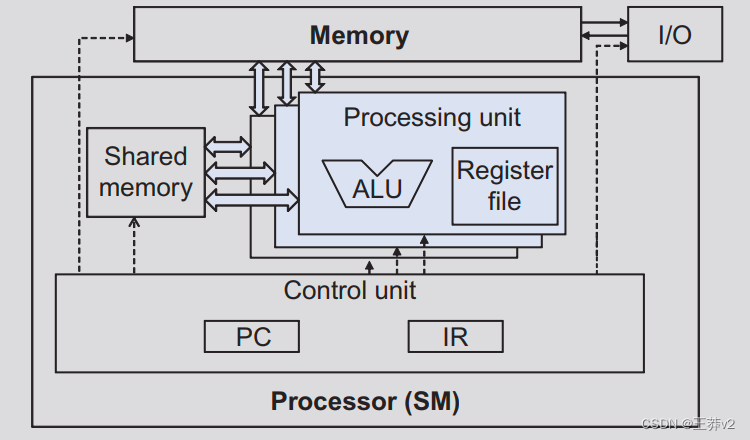
WARPS和SIMD硬件
下图说明了将线程作为warp执行的动机（与图4.8相同）。处理器只有一个控制单元来获取和解码指令。相同的控制信号传递到多个处理单元，每个处理单元在warp中执行一个线程。由于所有处理单元都由相同的指令控制，因此它们的执行差异是由于寄存器文件中的数据操作数值不同。在处理器设计中，这被称为单指令多数据（SIMD）。例如，尽管所有处理单元都由指令控制：r2和r3值在不同的处理单元中是不同的。
add r1, r2, r3

现代处理器中的控制单元相当复杂，包括用于获取指令的复杂逻辑和指令内存的访问端口。它们包括片上指令缓存，以减少指令获取的延迟。拥有多个处理单元来共享一个控制单元可以显著降低硬件制造成本和功耗。
随着处理器的功率越来越有限，新处理器可能会使用SIMD设计。事实上，未来我们可能会看到更多的处理单元共享一个控制单元。

线程块根据线程索引划分为warp。如果线程块被组织成一维数组，即只使用threadldx.x，则分区是直截了当的。ThreadIdx. warp中的x值是连续的，并且在增加。对于32的warp大小，warp 0 以线程0开始，以线程31结束，warp 1以线程32开始，以线程63结束。一般来说，warp n以线程32*n开始，以线程32（n+1）-1结束。对于大小不是32倍数的块，最后一个warp将用额外的线程填充，以填充32线程的位置。例如，如果一个块有48个线程，它将被分割成两个经线，其warp 1将用16个额外的线程填充。

对于由线程的多个维度组成的块，在划分为 warp 之前，维度将被投影到线性化的行大序中。线性顺序是通过将y和z坐标较大的行放在较低坐标的行之后确定的。也就是说，如果一个块由两个维度的线程组成，则通过将threadIdx.y为1的所有线程放在threadldx.y为0的线程之后，形成线性顺序。threadldx.y为2的线程将放在threadldx.y为1的线程之后，以此类推。

图5.12显示了将二维块的线程按线性顺序排列的示例。上部显示了块的二维视图。读者应该认识到与二维数组的行主要布局的相似性。每个线程显示为Tyx， x是threadldx.x，y是threadldx.y。图5.12的下半部分显示了块的线性化视图。前四个线程是那些threadldx.y值为0的线程；它们按增加的threadldx.x值排序。接下来的四个线程是线程Idx.y值为1的线程。它们也与增加的threadldx.x值一起放置。在这个例子中，所有16个线程都形成半个warp。warp将用另外16个线程填充，以完成32线程的warp。想象一个带有8x8线程的二维块。64个线程将形成两个warp。第一个warp以T0.0开头，以T3.7结束。第二个warp以T4.0开始，以T7.7结束。画出画面将是一个有用的练习。

对于三维块，我们首先将threadldx.z值为0的所有线程放入线性顺序。在这些线程中，它们被视为二维块，如图5.12.所示。然后，所有threadldx.z值为1的线程将被放入线性顺序，以此等。对于尺寸为2×8×4的三维螺纹块（x维度为4个，y维度为8个，z维度为2个），64个螺纹将分为两个warp，第一个经由T000到T0.7.3，第二个经由T1.0.0到T1.7.3在第二个warp。

SIMD硬件将warp的所有线程作为bundle执行。为同一warp中的所有线程运行指令。当warp中的所有线程在处理数据时遵循相同的执行路径，或者更正式地称为控制流时，它运行良好。例如，对于if-else构造，当所有线程执行if部分或全部执行其他部分时，执行效果良好。当warp中的线程采取不同的控制流路径时，SIMD硬件将多次通过这些发散路径。一个通道执行那些跟随if部分的线程，另一个通道执行那些跟随其他部分的线程。在每次通过期间，遵循其他路径的线程不允许生效。这些传递是相互连续的，因此会增加执行时间。

发散warp执行的多通道方法扩展了SIMD硬件实现CUDA线程完整语义的能力。虽然硬件对warp中的所有线程执行相同的指令，但它有选择地让线程仅在每个通道中生效，允许每个线程采取自己的控制流路径。这保留了线程的独立性，同时利用了SIMD硬件成本的降低。

当同一warp中的线程遵循不同的执行路径时，我们说这些线程在执行中会发散。在if-else示例中，如果warp中的一些线程采取if路径，而一些线程采取else路径，就会出现分歧。发散的成本是硬件需要采取的额外通道，以便允许warp中的线程做出自己的决定。

发散也可能出现在其他结构中，例如，如果warp中的线程执行for-loop，可以为不同的线程进行六次、七次或八次遍。所有线程将一起完成前六次迭代。两个通道将用于执行第七次迭代，一个用于那些接受迭代的人，一个用于那些不接受迭代的人。将使用两个通道来执行第八次的迭代，一个用于那些接受迭代的人，一个用于那些不接受迭代的人。

人们可以通过检查其决策条件来确定控制结构是否会导致线程发散。如果决策条件基于threadIdx值，则控制语句可能会导致线程发散。例如，语句如果（threadldx.x > 2）{}导致线程遵循两个不同的控制流路径。线程0、1和2遵循的路径与线程3、4、5等不同。同样，如果循环条件基于线程索引值，则循环可能会导致线程发散。

使用具有线程发散的控件结构的一个常见原因是在将线程映射到数据时处理边界条件。这通常是因为线程总数需要是块大小的倍数，而数据的大小可以是任意数字。从图2.12中的矢量加法内核开始。我们在addVecKernel中有一个if（i<n）语句。这是因为并非所有向量长度都可以表示为块大小的倍数。例如，假设矢量长度为1003。假设我们选择了64作为块大小。需要启动16个线程块来处理所有1003个矢量元素。然而，这16个线程块将有1024个线程。我们需要禁用线程块15中的最后21个线程，使其无法进行原始程序预期/不允许的工作。请记住，这16个块被划分为32个翘曲。只有最后的warp才会有控制分歧。

请注意，控制发散的性能影响随着正在处理的向量的大小而减少。对于矢量长度为100，四个warp中的一个将具有控制发散，这可能会对性能产生重大影响。对于1000的矢量大小，32个warp中只有一个会有控制发散。也就是说，控制分歧只会影响约3%的执行时间。即使它使warp的执行时间增加一倍，对总执行时间的净影响约为3%。显然，如果矢量长度为10,000或更多，313个翘曲中只有一个会有控制发散。控制分歧的影响将远低于1%！

对于二维数据，例如颜色到灰度转换示例，if-语句也用于处理在数据边缘运行的线程的边界条件。在图3.2中，为了处理76×62的图片，我们使用了20 = 5*4个二维块，每个块由16×16个线程组成。每个块将被分割成8个warp，每个块由两行块组成。总共涉及160个warp（每块8个warp）。

要分析控制分歧的影响，请参阅图3.5.。1区12个区块的warp都不会有控制分歧。区域1有12*8=96个warp。对于区域2，所有24个翘曲都有控制发散。对于区域3，请注意，所有底部warp都映射到完全在图片之外的数据。因此，他们中没有人会通过if条件。读者应该验证，如果图片在垂直尺寸中具有奇数像素，这些warp会有控制发散。由于它们都遵循相同的控制流路径，这32个warp都不会有控制发散！在第4区，前七个warp将有控制分歧，但最后一个warp不会。总而言之，160个warp中有31个将具有控制分歧。

控制分歧的性能影响再次随着水平维度像素数量的增加而减少。例如，如果我们处理一张带有16x16块的200×150图片，总共会有130=1310个线程块或1040个warp。区域1至4的warp数量为864（1298）、72（98）、96（128）和8（18）。这些warp中只有80个会有控制分歧。因此，控制分歧的性能影响将小于8%。显然，如果我们处理水平尺寸超过1000像素的真实图片，控制发散的性能影响将小于2%。

控制分歧也自然出现在一些重要的并行算法中，其中参与计算的线程数量会随着时间的推移而变化。我们将使用reduction算法来说明这种行为。

还原算法从值数组中导出单个值。单个值可以是所有元素中的总和、最大值、最小值等。所有这些类型的还原都具有相同的计算结构。通过按顺序检查数组的每个元素，可以很容易地完成还原。当访问一个元素时，要采取的行动取决于正在执行的还原类型。对于总和减少，在当前步骤中访问的元素的值或当前值被添加到运行的总和中。对于最大还原，将当前值与迄今为止访问的所有元素的运行最大值进行比较。如果当前值大于运行的最大值，则当前元素值将成为运行的最大值。为了最小的减少，将当前正在访问的元素的值与运行的最小值进行比较。如果当前值小于运行最小值，则当前元素值变为运行最小值。当所有元素都被访问时，顺序的gorithm就结束了。

顺序还原算法是高效的，因为每个元素只访问一次，并且在访问每个元素时只执行最少的工作量。它的执行时间与所涉及的元素数量成正比。也就是说，算法的计算复杂度是O（N），其中N是参与约简的元素数量。

访问大数组中所有元素所需的时间激发了并行执行。并行还原算法通常类似于足球锦标赛的结构。事实上，世界杯的淘汰过程是减少“最大值，其中最大值被定义为“击败”所有其他球队的球队。锦标赛“减少”分多轮完成。团队是成对的。在第一轮比赛中，所有配对都并行比赛。第一轮的获胜者晋级第二轮，其获胜者晋级第三轮等。随着16支球队参加锦标赛，第一轮将选出八支获胜者，第二轮将选出四支队伍，第三轮将选出两支获胜者，第四轮将选出一名最终获胜者。

应该很容易看出，即使有1024支球队，也只需要10轮就能确定最终的获胜者。诀窍是有足够的足球场，在第一轮中并行举行512场比赛，第二轮举行256场比赛，第三轮举行128场比赛，以此类。有足够的场地，即使有6万支球队，我们也可以在短短16轮内确定最终获胜者。当然，一个人需要有足够的足球场和足够的官员来容纳第一轮的三万场比赛等。

图5.13显示了一个执行并行求和还原的内核函数。原始数组在全局内存中。每个线程块通过将该部分的元素加载到共享内存中并对这些元素执行并行减少来减少数组的一个部分。代码将输入数组X的元素从global内存加载到共享内存中。减少是原地完成的，这意味着共享内存中的一些元素将被部分和所取代。内核函数中for-loop的每次迭代都会实现一轮还原。

For-loop中的__syncthreads（）语句（第5行）确保在允许任何线程开始当前迭代之前，已生成之前生成所有部分总和。这样，所有进入第二次迭代的线程都将使用第一次迭代中生成的值。第一轮后，偶数元素将被第一轮生成的部分和所取代。第二轮后，指数为四倍数的元素将替换为部分和。最后一轮结束后，整个部分的总和将在partialSum[0]。
在图5.13中，第3行将步长变量初始化为1。在第一次迭代中，第6行中的if-statement用于仅选择偶数线程，以在两个相邻元素之间执行加法。内核的执行如图5.14.所示。线程和数组元素值以水平方向显示。线程的迭代以垂直方向显示，时间从上到下。每行图5.14在for-loop迭代后显示数组元素的内容。

如图5.16所示，数组的偶数元素在迭代1后保存成对的部分和。在第二次迭代之前，步幅变量的值翻倍为2。在第二次迭代中，只有索引为四倍数的线程才会在第7行中执行添加状态。每个线程生成四个元素的部分总和，如第2行所示。每个部分有512个元素，内核函数将在9次迭代后生成整个部分的总和。通过使用blockDim.x作为第4行中绑定的循环，内核假设其启动的线程数量与该部分中的元素数量相同。也就是说，对于512个部分大小，内核需要使用512个线程启动。

让我们分析一下内核完成的总工作量。假设要减少的元素总数为N。第一轮需要N/2的添加。第二轮需要N/4的添加。最后一轮只有一个补充。有logz（N）回合。内核执行的加法总数为N/2 + N/4+ N/8 + …+ 1 = N-1。因此，还原算法的计算复杂度是O（N）。该算法工作效率高。然而，我们还需要确保在执行内核时有效利用硬件。

图5.13中的内核显然有线程分歧。在循环的第一次迭代中，只有那些线程ldx.x均匀的线程才会执行addstatement。执行这些线程需要一个通道，需要一个额外的通道来执行那些不执行第7行的线程。在每次连续的迭代中，将更少的线程将执行第7行，但在每次迭代期间仍然需要两个通道来执行所有线程。这种发散可以通过对a.gorithm的轻微改变来减少。

图5.15显示了一个修改后的内核，其总和减少算法略有不同。它没有在第一轮中添加邻居元素，而是添加彼此相距半部分的元素。它通过将步幅初始化为截面的一半大小来做到这一点。第一轮添加的所有对都是部分尺寸的一半。第一次迭代后，所有成对的和都存储在数组的前半部分，如图5.16.所示。在进入下一个迭代之前，循环将步幅除以2。因此，对于第二次迭代，步幅变量值是截面尺寸的四分之一。也就是说，在第二次迭代期间，线程会添加彼此相隔四分之一的元素。
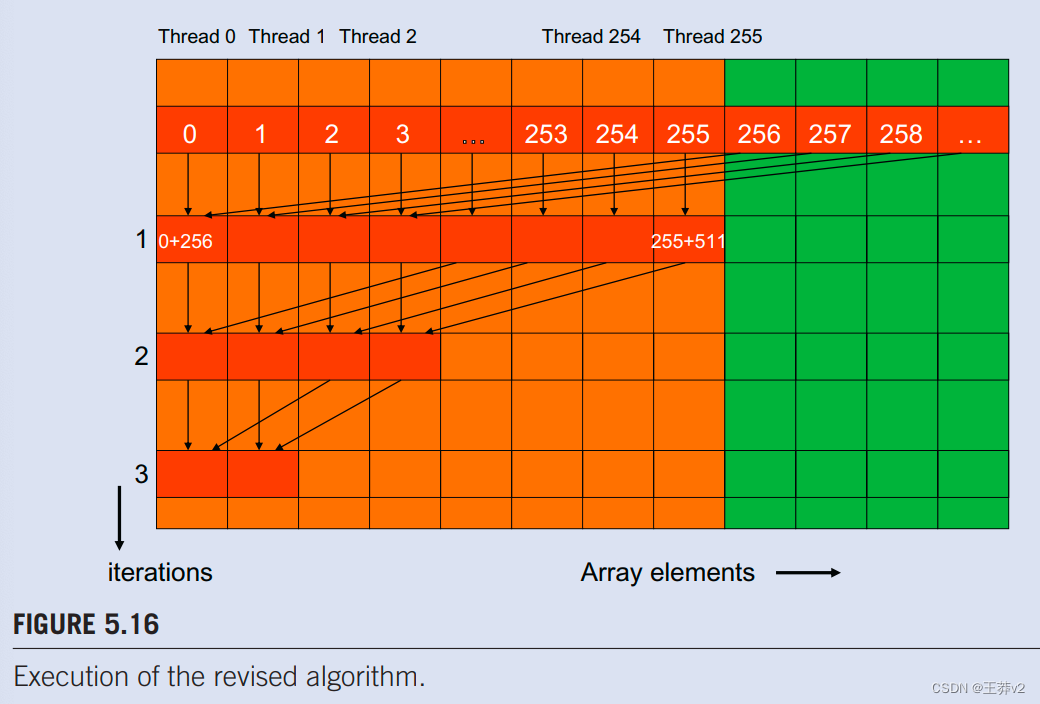请注意，图5.15中的内核。仍然有一个if-statement（循环中的第6行）。每次迭代中执行第7行的线程数量与图5.13.中相同。那么，为什么两个内核之间会有性能差异呢？答案在于执行第7行的线程相对于不执行的线程的位置。

图5.16说明了图5.15.中修订内核的执行情况。在第一次迭代中，所有线程ldx.x值小于节大小一半的线程都会执行第7行。对于512个元素的部分，线程0到255在第一次迭代中执行添加状态，而线程256到511不执行。配对总和在第一次迭代后存储在元素0到255中。由于warp由32个具有连续threadldx.x值的线程组成，因此从warp到warp7的所有线程都执行添加状态，而warp8到warp15都跳过添加状态。由于每个warp中的所有线程都走相同的路径，因此没有线程发散！

图5.15中的内核。并不能完全消除由if-statement引起的分歧。读者应验证，从第5次迭代开始，执行第7行的线程数将低于32。也就是说，最后五次迭代将只有16、8、4、2和1个线程（s）执行加法。这意味着内核执行在这些迭代中仍将存在差异。然而，有发散的循环迭代次数从十次减少到五次。

图5.13和5.15之间的区别很小，但对性能有非常显著的影响。它需要对设备SIMD硬件上的线程执行有明确了解的人能够自信地进行此类调整。

---

在CUDA编程中，warp是执行指令的基本单位，由一组（通常是32个）线程组成。当这些线程执行相同的指令时，GPU的效率最高。然而，如果线程在同一个warp中需要执行不同的指令路径（即发生分支），这就会导致warp分歧（warp divergence）。当warp分歧发生时，GPU必须串行执行每个不同的分支路径，这降低了执行效率。

减少warp分歧的一种常见方法是重构代码，以减少条件分支或确保同一warp中的所有线程都遵循相同的执行路径。在某些算法中，如归约求和（reduction sum），可以通过特定的设计模式来减少分歧。

归约求和是将所有元素的值加在一起以得到单个总和的过程。在GPU上执行归约求和时，可以采用以下策略来减少warp分歧：

1. 使用循环展开和步进减少：
通过循环展开，可以减少循环迭代次数，并且每次迭代处理更多的数据。步进减少意味着在每个迭代中，线程读取的元素索引之间的距离逐渐增加。这可以确保更多的线程在每次迭代中执行相同的操作，从而减少分歧。

2. 利用共享内存：
在归约求和过程中，使用共享内存可以减少全局内存访问，因为共享内存的访问速度比全局内存快得多。通过让warp中的线程先将数据加载到共享内存，然后在共享内存上执行归约操作，可以减少不必要的分歧。

3. 使用内建函数：
CUDA提供了一些内建函数（如__shfl_down_sync），这些函数可以在warp内部线程之间进行高效的数据交换，而不需要显式的共享内存访问。这些函数有助于减少不同线程间的控制流分歧。

4. 尽量避免跨warp的同步：
在归约求和中，如果需要跨warp的同步，尽量设计算法使得同步操作次数最小化。例如，可以在每个block内部完成尽可能多的工作，然后只在block之间进行最终的同步和求和。

5. 优化线程分配：
确保每个warp处理的数据量是均匀的，这样可以避免一些warp提前完成任务而其他warp还在执行计算，从而减少分歧。

下面是一个简化的归约求和的例子，展示了如何使用共享内存和循环展开来减少warp分歧：

__global__ void reduceSum(float *input, float *output, int n) {
    extern __shared__ float sdata[];

    // 每个线程加载一个元素到共享内存
    unsigned int tid = threadIdx.x;
    unsigned int i = blockIdx.x * blockDim.x + threadIdx.x;
    sdata[tid] = (i < n) ? input[i] : 0;
    __syncthreads();

    // 归约求和，每次迭代步长翻倍
    for (unsigned int s = blockDim.x / 2; s > 0; s >>= 1) {
        if (tid < s) {
            sdata[tid] += sdata[tid + s];
        }
        __syncthreads();
    }

    // 将结果写回全局内存
    if (tid == 0) output[blockIdx.x] = sdata[0];
}

在这个例子中，首先将数据加载到共享内存，然后使用循环展开来减少迭代次数，并在每次迭代中减少步长，这样每个warp中的线程都在执行相同的操作，减少了warp分歧。最后，每个block的归约结果被写入全局内存中。