Codeforces Good Bye 2023 题解 | JorbanS
A - 2023
void solve() {
cin >> n >> k;
ll res = 1;
while (n --) {
int x; cin >> x;
res *= x;
}
if (2023 % res) {
cout << no << endl;
return;
}
cout << yes << endl;
cout << 2023 / res << ' ';
k --;
while (k --) cout << 1 << ' ';
cout << endl;
}
B - Two Divisors
题解 先尝试让 l c m ( a , b ) lcm(a, b) lcm(a,b) 作为 x x x。若 x = l c m ( a , b ) x=lcm(a, b) x=lcm(a,b),此时 b = a × p b=a\times p b=a×p, p p p 为 x x x 的最小素因子,因此 x = b × p = b × b a x=b\times p=b\times\frac b a x=b×p=b×ab?
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
int solve() {
int a, b; cin >> a >> b;
if (a > b) swap(a, b);
int d = gcd(a, b);
int res = a / gcd(a, b) * b;
return res == b ? res / a * b : res;
}
C - Training Before the Olympiad
题意 A A A 先取要使得最后剩下的数最大, B B B 后取要使得数最小
题解 B B B 每次优先取一奇一偶
若 A A A 优先取两偶,进行操作后加上去的永远是偶数,因此每一轮多两个偶数,偶数的数量永远不能穷尽,则 B B B 的取法不受 A A A 的限制,故不是最优的
故 A A A 优先取奇数,每轮少三个奇数多两个偶数,奇数能够穷尽,故看最后有几个奇数
- 若还剩 0 0 0 个,不需要考虑
- 若还剩 1 1 1 个,则一定会取一奇一偶
- 若还剩 2 2 2 个,则 A A A 取两个奇数使得奇数清零
int n, a[N], odd[N], even[N];
void solve() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= n; i ++) odd[i] = even[i] = 0;
for (int i = 1; i <= n; i ++) {
odd[i] = odd[i - 1];
even[i] = even[i - 1];
if (a[i] & 1) odd[i] ++;
else even[i] ++;
}
ll sum = a[1];
cout << a[1] << ' ';
for (int i = 2; i <= n; i ++) {
sum += a[i];
int res = odd[i] / 3;
odd[i] %= 3;
res += odd[i] & 1;
cout << sum - res << ' ';
}
cout << endl;
}
D - Mathematical Problem
题解 打表找规律
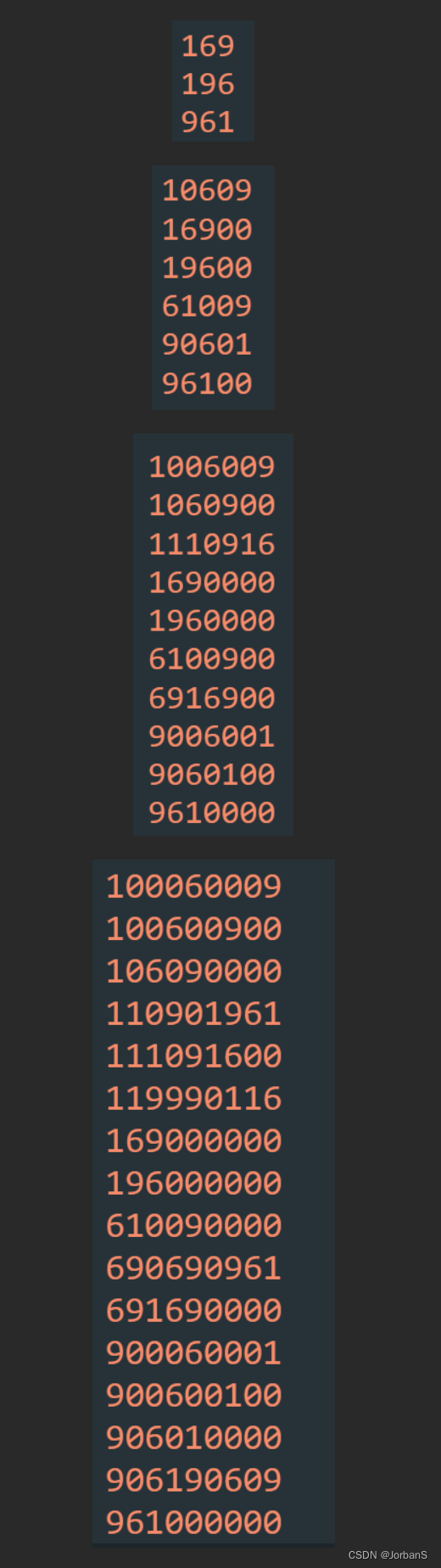
打表 c o d e code code
#define int long long
void solve() {
auto digit = [](int x) {
vector<int> a;
set<int> s;
while (x) {
int t = x % 10;
if (!s.count(t)) a.push_back(t), s.insert(t);
x /= 10;
}
sort(a.begin(), a.end());
return a;
};
int n; cin >> n;
map<vector<int>, vector<int>> mp;
for (int i = sqrt(pow(10, n - 1)); i <= sqrt(pow(10, n)); i ++)
if (to_string(i * i).size() == n)
mp[digit(i * i)].push_back(i * i);
for (auto [x, c] : mp)
if (c.size() >= n) {
for (auto i : c)
cout << i << endl;
cout << endl;
}
}
题目 c o d e code code
int n;
int a[2][3] = {
{1, 6, 9},
{9, 6, 1},
};
#define loop(x) for (int _ = 0; _ < x; _ ++) cout << 0;
void solve() {
cin >> n;
if (n == 1) {
cout << 1 << endl;
return;
}
cout << 196;
loop(n - 3);
cout << endl;
int cnt = 1;
for (int j = 0; j <= (n - 1) / 2 - 1; j ++) {
for (int i = 0; i < 2; i ++) {
if (cnt == n) return;
cout << a[i][0];
loop(j);
cout << a[i][1];
loop(j);
cout << a[i][2];
loop(n - j * 2 - 3);
cout << endl;
cnt ++;
}
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 中国社科院-新加坡新跃社科大学工商管理博士(DBA)项目课程设置
- HashMap的五种遍历方式
- C语言学习笔记 : 无符号类型 unsigned 与 unsigned int 是否一样
- 基于Java校园考试信息系统
- issue queue的实现方式
- 【Frontiers】“神仙期刊”,JCR1区,发文量3000+,录用率75%,1-2个月录用!
- 大象机器人发布万元级水星Mercury人形机器人产品系列,联结未来,一触即达!
- 编程笔记 html5&css&js 019 HTML实体
- RequestMapping注解的使用和常见的GET和POST请求方式
- 021-信息打点-公众号服务&Github监控&供应链&网盘泄漏&证书图标邮箱资产