深度学习记录--学习率衰减(learning rate decay)

发布时间：2024年01月21日

学习率衰减

mini-batch梯度下降最终会在最小值附近的区间摆动(噪声很大)，不会精确收敛

为了更加近似最小值，采用学习率衰减的方法

随着学习率的衰减，步长会逐渐变小，因此最终摆动的区间会很小，更加近似最小值

如下图，蓝色曲线表示mini-batch梯度下降，绿色曲线表示采用学习率衰减的梯度下降

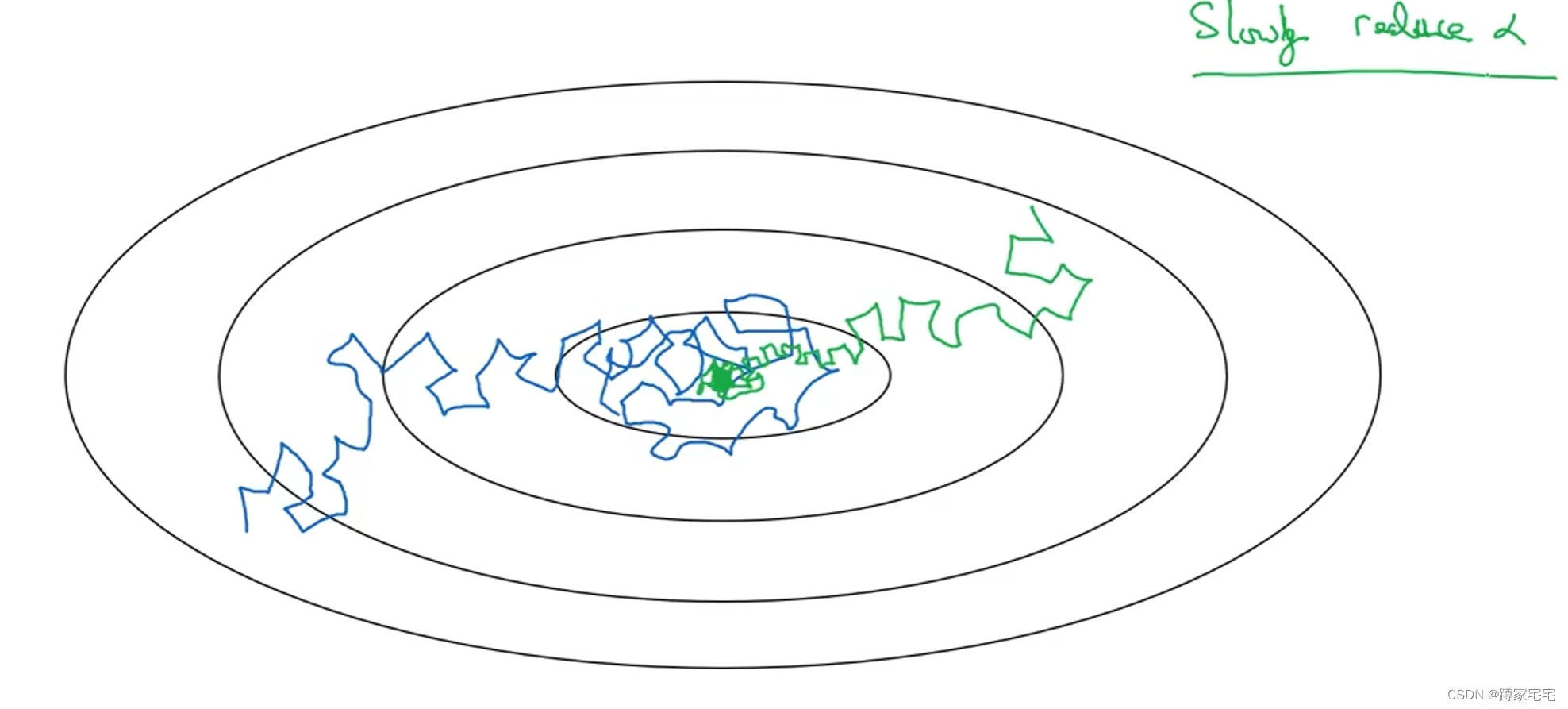
学习率衰减的实现

1 epoch = 遍历数据1次

$\alpha = \frac{1}{1+rate_{decay}*num_{epoch}} *\alpha_{0}$

$rate_{decay}$ 是学习率衰减的超参数， $\alpha_{0}$ 是初始学习率， $num_{epoch}$ 是遍历次数

其他衰减方案

$\alpha = \varepsilon ^{num_{epoch}}*\alpha_{0}$

$\alpha_{0}$ 是初始学习率， $\varepsilon$ 是衰减常量，一般设置 $\varepsilon=0.95$ ， $num_{epoch}$ 是遍历次数

$\alpha = \frac{k}{\sqrt{num_{epoch}}} *\alpha_{0}$

$\alpha_{0}$ 是初始学习率， $k$ 是衰减常量， $num_{epoch}$ 是遍历次数

分段衰减函数

文章来源:https://blog.csdn.net/Xudong_12345/article/details/135731758
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！