AI嵌入式K210项目（17）-快速傅里叶变换加速器 (FFT)

---

前言

K210内置了丰富的加速器，包括神经网络处理器 (KPU)，AES(高级加密加速器)，APU 麦克风阵列语音数据加速计算处理器，现场可编程 IO 阵列 (FPIOA)，数字摄像头接口 (DVP)，相对于软件可以极大的提高 AES 运算速度，快速傅里叶变换加速器 (FFT)，安全散列算法加速器 (SHA256)。
本文介绍内置的快速傅里叶变换加速器 (FFT)；

一、什么是傅里叶变换？

傅里叶变换（Fourier Transform）可以将一个在时间（或空间）域内的信号转换成频率域内的信号。其物理意义是将一个信号分解为不同频率的正弦波组成的谱，从而揭示了信号的频率特性。它的物理意义在于将信号从时间域转换到频率域，帮助我们理解信号的频率特性。
物理意义
傅里叶变换可以将一个信号分解为不同频率的正弦波组成的谱，从而揭示信号的频率特性。通过傅里叶变换，我们能够更好地理解声音、图像等信号的组成和特性。例如，在声音处理中，傅里叶变换可以将声音信号转换为频域信号，进而分析不同音调所对应的频率成分。这对于音频质量改善、音乐合成和语音识别等方面有着重要作用。

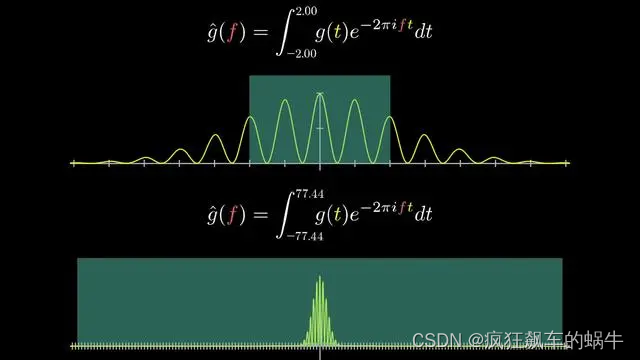
在物理学、工程和科学领域，许多信号都可以表示为不同频率的正弦波的叠加。傅里叶变换能够帮助我们理解这些信号的频率特性，并提供有效的信号处理和分析方法。例如，在图像处理中，傅里叶变换可用于图像压缩、边缘检测等处理，为数字图像处理提供重要支持。

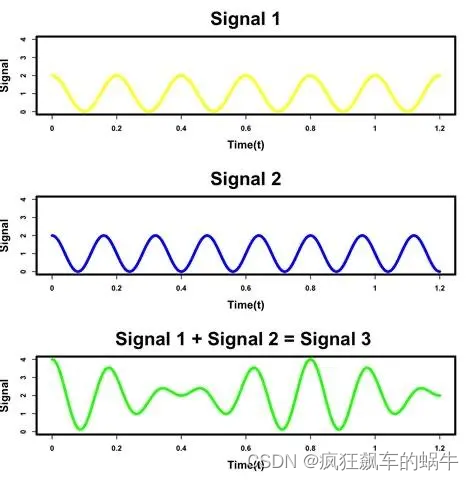
傅里叶变换非常重要，在音视频处理，通讯等领域有着重要的应用，大家可以通过其他方式好好学习一下，

快速傅里叶变换(FFT)即利用计算机计算离散傅里叶变换（DFT）的高效、快速计算方法的统称,快速傅里叶变换在运算速度和适用范围方面具有优势，而傅里叶变换在精度和计算方式方面更优。

二、K210的快速傅里叶变换加速器

K210内置快速傅立叶变换加速器FFT Accelerater。该模块可以支持64 点、128 点、256 点以及512 点的FFT 以及IFFT。在FFT 内部有两块大小为512*32bit 的SRAM，在配置完成后FFT 会向DMA 发送TX 请求，将DMA 送来的送据放到其中的一块SRAM 中去，直到满足当前FFT 运算所需要的数据量并开始FFT 运算，蝶形运算单元从包含有有效数据的SRAM 中读出数据，运算结束后将数据写到另外一块SRAM 中去，下次蝶形运算再从刚写入的SRAM 中读出数据，运算结束后并写入另外一块SRAM，如此反复交替进行直到完成整个FFT 运算。

FFT 加速器是用硬件的方式来实现FFT 的基2 时分运算。

? 支持多种运算长度，即支持64 点、128 点、256 点以及512 点运算

? 支持两种运算模式，即FFT 以及IFFT 运算

? 支持可配的输入数据位宽，即支持32 位及64 位输入

? 支持可配的输入数据排列方式，即支持虚部、实部交替，纯实部以及实部、虚部分离三种数据排

列方式

? 支持DMA 传输

对应的头文件 aes.h

为用户提供以下接口：

? fft_complex_uint16_dma：FFT运算。

实验过程

本实验使用K210自带的FFT加速器和开源软FFT做对比，看一下加速效果。使用的fft开源库，大家可以网上下载，或者到我gitee上下载，这里只贴man.c部分内容了；

#include <math.h>
#include <stdlib.h>
#include <stdio.h>
#include "encoding.h"
#include "dmac.h"
#include "fft.h"
#include "encoding.h"
#include "sysctl.h"
#include "fft_soft.h"

#define FFT_N               512U
#define FFT_FORWARD_SHIFT   0x0U
#define FFT_BACKWARD_SHIFT  0x1ffU
#define PI                  3.14159265358979323846

typedef enum _complex_mode
{
    FFT_HARD = 0,
    FFT_SOFT = 1,
    FFT_COMPLEX_MAX,
} complex_mode_t;

int16_t real[FFT_N];
int16_t imag[FFT_N];
float hard_power[FFT_N];
float soft_power[FFT_N];
float hard_angel[FFT_N];
float soft_angel[FFT_N];
uint64_t fft_out_data[FFT_N / 2];
uint64_t buffer_input[FFT_N];
uint64_t buffer_output[FFT_N];
uint64_t cycle[FFT_COMPLEX_MAX][FFT_DIR_MAX];

uint16_t get_bit1_num(uint32_t data)
{
    uint16_t num;
    for (num = 0; data; num++)
        data &= data - 1;
    return num;
}

int main(void)
{
    int32_t i;
    float tempf1[3];
    fft_data_t *output_data;
    fft_data_t *input_data;
    uint16_t bit1_num = get_bit1_num(FFT_FORWARD_SHIFT);
    complex_hard_t data_hard[FFT_N] = {0};
    complex data_soft[FFT_N] = {0};
    /* 取得一组复数 */
    for (i = 0; i < FFT_N; i++)
    {
        tempf1[0] = 0.3 * cosf(2 * PI * i / FFT_N + PI / 3) * 256;
        tempf1[1] = 0.1 * cosf(16 * 2 * PI * i / FFT_N - PI / 9) * 256;
        tempf1[2] = 0.5 * cosf((19 * 2 * PI * i / FFT_N) + PI / 6) * 256;
        data_hard[i].real = (int16_t)(tempf1[0] + tempf1[1] + tempf1[2] + 10);
        data_hard[i].imag = (int16_t)0;
        data_soft[i].real = data_hard[i].real;
        data_soft[i].imag = data_hard[i].imag;
    }

    /* 复数转化成傅里叶数据结构RIRI */
    for (int i = 0; i < FFT_N / 2; ++i)
    {
        input_data = (fft_data_t *)&buffer_input[i];
        input_data->R1 = data_hard[2 * i].real;
        input_data->I1 = data_hard[2 * i].imag;
        input_data->R2 = data_hard[2 * i + 1].real;
        input_data->I2 = data_hard[2 * i + 1].imag;
    }
    
    /* 硬件处理FFT数据，并记录时间 */
    cycle[FFT_HARD][FFT_DIR_FORWARD] = read_cycle();
    fft_complex_uint16_dma(DMAC_CHANNEL0, DMAC_CHANNEL1, FFT_FORWARD_SHIFT, FFT_DIR_FORWARD, buffer_input, FFT_N, buffer_output);
    cycle[FFT_HARD][FFT_DIR_FORWARD] = read_cycle() - cycle[FFT_HARD][FFT_DIR_FORWARD];

    /* 软件处理FFT数据，并记录时间 */
    cycle[FFT_SOFT][FFT_DIR_FORWARD] = read_cycle();
    fft_soft(data_soft, FFT_N);
    cycle[FFT_SOFT][FFT_DIR_FORWARD] = read_cycle() - cycle[FFT_SOFT][FFT_DIR_FORWARD];
    
    /* 解析计算输出的数据 */
    for (i = 0; i < FFT_N / 2; i++)
    {
        output_data = (fft_data_t*)&buffer_output[i];
        data_hard[2 * i].imag = output_data->I1 ;
        data_hard[2 * i].real = output_data->R1 ;
        data_hard[2 * i + 1].imag = output_data->I2 ;
        data_hard[2 * i + 1].real = output_data->R2 ;
    }

    /* 复数取模 */
    for (i = 0; i < FFT_N; i++)
    {
        hard_power[i] = sqrt(data_hard[i].real * data_hard[i].real + data_hard[i].imag * data_hard[i].imag) * 2;
        soft_power[i] = sqrt(data_soft[i].real * data_soft[i].real + data_soft[i].imag * data_soft[i].imag) * 2;
    }

    /* 打印软件和硬件复数的实部和虚部 */
    printf("\n[hard fft real][soft fft real][hard fft imag][soft fft imag]\n");
    for (i = 0; i < FFT_N / 2; i++)
        printf("%3d:%7d %7d %7d %7d\n",
                i, data_hard[i].real, (int32_t)data_soft[i].real, data_hard[i].imag, (int32_t)data_soft[i].imag);

    printf("\nhard power  soft power:\n");
    printf("%3d : %f  %f\n", 0, hard_power[0] / 2 / FFT_N * (1 << bit1_num), soft_power[0] / 2 / FFT_N);
    for (i = 1; i < FFT_N / 2; i++)
        printf("%3d : %f  %f\n", i, hard_power[i] / FFT_N * (1 << bit1_num), soft_power[i] / FFT_N);

    /* 打印相位 */
    printf("\nhard phase  soft phase:\n");
    for (i = 0; i < FFT_N / 2; i++)
    {
        hard_angel[i] = atan2(data_hard[i].imag, data_hard[i].real);
        soft_angel[i] = atan2(data_soft[i].imag, data_soft[i].real);
        printf("%3d : %f  %f\n", i, hard_angel[i] * 180 / PI, soft_angel[i] * 180 / PI);
    }

    /* 快速傅里叶变换逆运算 */
    for (int i = 0; i < FFT_N / 2; ++i)
    {
        input_data = (fft_data_t *)&buffer_input[i];
        input_data->R1 = data_hard[2 * i].real;
        input_data->I1 = data_hard[2 * i].imag;
        input_data->R2 = data_hard[2 * i + 1].real;
        input_data->I2 = data_hard[2 * i + 1].imag;
    }

    /* 硬件和软件快速傅里叶变换运算 */
    cycle[FFT_HARD][FFT_DIR_BACKWARD] = read_cycle();
    fft_complex_uint16_dma(DMAC_CHANNEL0, DMAC_CHANNEL1, FFT_BACKWARD_SHIFT, FFT_DIR_BACKWARD, buffer_input, FFT_N, buffer_output);
    cycle[FFT_HARD][FFT_DIR_BACKWARD] = read_cycle() - cycle[FFT_HARD][FFT_DIR_BACKWARD];
    cycle[FFT_SOFT][FFT_DIR_BACKWARD] = read_cycle();
    ifft_soft(data_soft, FFT_N);
    cycle[FFT_SOFT][FFT_DIR_BACKWARD] = read_cycle() - cycle[FFT_SOFT][FFT_DIR_BACKWARD];
    
    for (i = 0; i < FFT_N / 2; i++)
    {
        output_data = (fft_data_t*)&buffer_output[i];
        data_hard[2 * i].imag = output_data->I1 ;
        data_hard[2 * i].real = output_data->R1 ;
        data_hard[2 * i + 1].imag = output_data->I2 ;
        data_hard[2 * i + 1].real = output_data->R2 ;
    }

    printf("\n[hard ifft real][soft ifft real][hard ifft imag][soft ifft imag]\n");
    for (i = 0; i < FFT_N / 2; i++)
        printf("%3d:%7d  %7d %7d %7d\n",
                i, data_hard[i].real, (int32_t)data_soft[i].real, data_hard[i].imag, (int32_t)data_soft[i].imag);

    printf("[hard fft test] [%d bytes] forward time = %ld us, backward time = %ld us\n",
            FFT_N,
            cycle[FFT_HARD][FFT_DIR_FORWARD]/(sysctl_clock_get_freq(SYSCTL_CLOCK_CPU)/1000000),
            cycle[FFT_HARD][FFT_DIR_BACKWARD]/(sysctl_clock_get_freq(SYSCTL_CLOCK_CPU)/1000000));

    printf("[soft fft test] [%d bytes] forward time = %ld us, backward time = %ld us\n",
            FFT_N,
            cycle[FFT_SOFT][FFT_DIR_FORWARD]/(sysctl_clock_get_freq(SYSCTL_CLOCK_CPU)/1000000),
            cycle[FFT_SOFT][FFT_DIR_BACKWARD]/(sysctl_clock_get_freq(SYSCTL_CLOCK_CPU)/1000000));
    while (1)
        ;
    return 0;
}

代码完成后，进行编译

cd build

cmake .. -DPROJ=fft -G "MinGW Makefiles"

make

编译完成后，在build文件夹下会生成fft.bin文件。

使用type-C数据线连接电脑与K210开发板，打开kflash，选择对应的设备，再将程序固件烧录到K210开发板上。

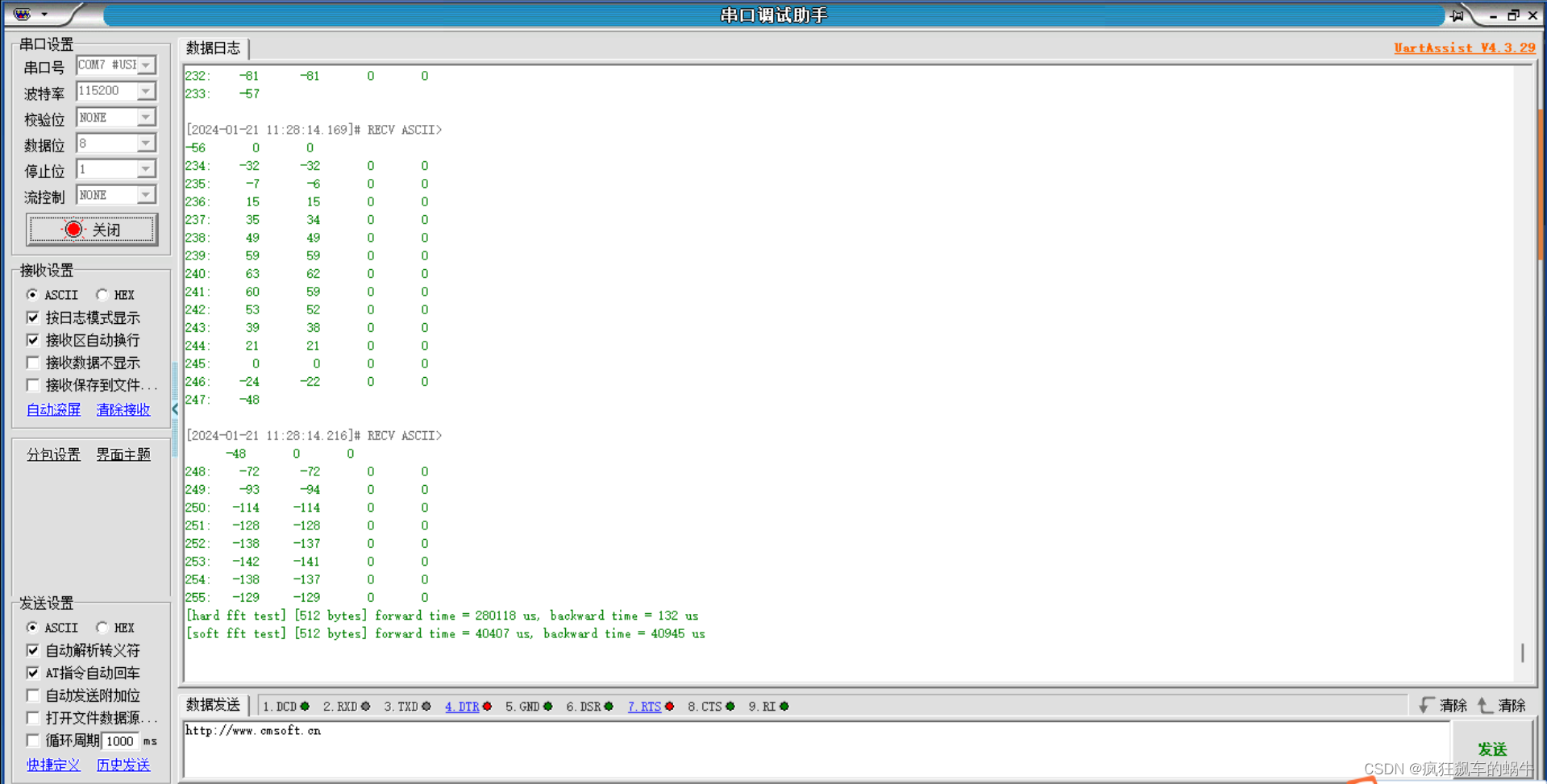
烧录后重启开发板，实验结果如下：

---

总结

从实验结果来看内置的快速傅里叶变换加速器 (FFT)速度是软FFT的300多倍，加速效果非常明显。