1.3进制，码（8421），化简规则、卡诺图化简、性质，触发器（转换与设计、应用），电路图，电路设计

十进制与原码、反码、补码之间的转换

正数的原码、反码、补码相同，符号位为0

负数的原码为、符号位+1，+二进制数

反码，符号位不变、其它取反，

补码为：反码最低有效位+1?

运算

卡诺图化简

奇偶校验码

检查1的个数，如果是奇数个，就在头部填充0，是偶数个就填充1

总之就是奇偶校验码就要检验其中的1的个数是奇数还是偶数，并维持不变，奇数校验码就要保持奇数个，偶数就要保持偶数个

8421码

8421码就是用4位二进制表示1位10进制，相当于16进制，但不是16进制，因为高于10的部分都会直接废掉不用

触发器

触发器基本的是要建立次态与现态之间的关系，就是Qn+1与Qn之间的关系?

触发器转换??

JK到RS?

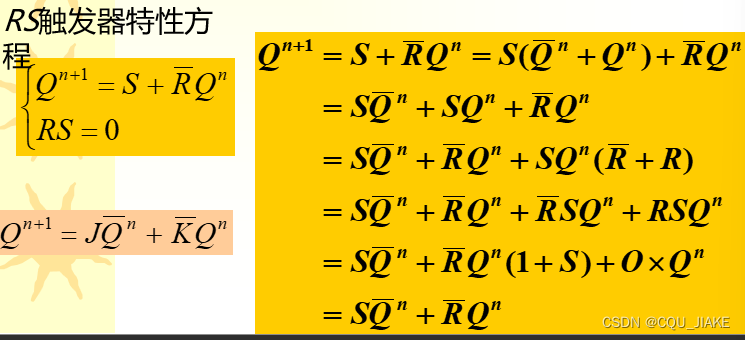
展开S，再利用特征约束，RS=0，即完成化简?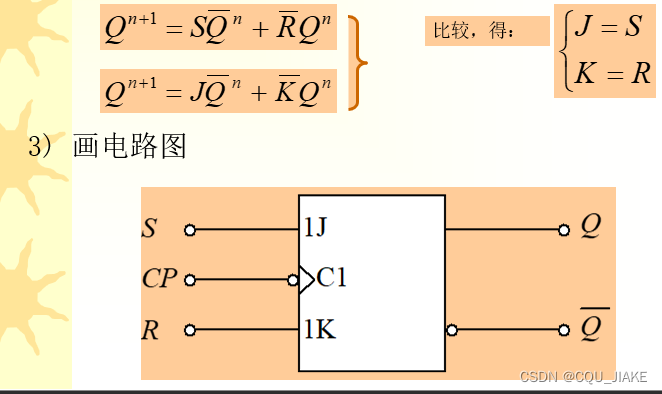

JK到D

?改到D，就是说，外部输入的信号就只有一个D输入端口，然后这个输入的信号通过内部的改造，即实现内部的JK，实现其功能，用D信号接到JK触发器的接口上，来实现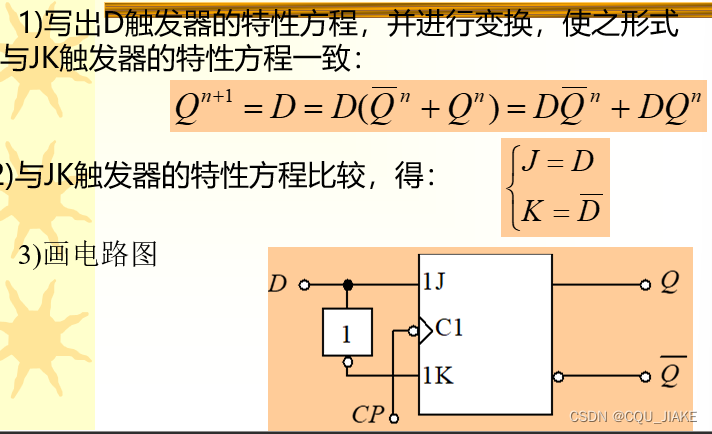

JK到T?

就是说外部只有一个T信号，然后方程是当前现态的一个反转，为1则反转，不为1则保持，就是T异或上现在的信号，那就是T信号直接输入到JK信号上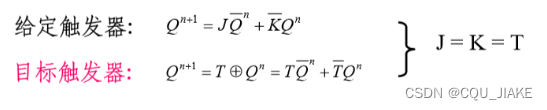

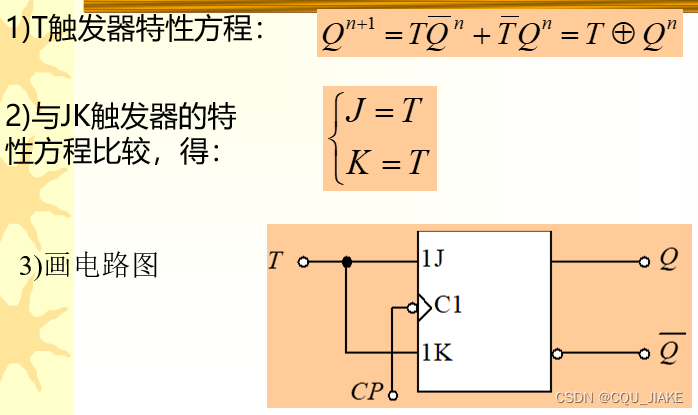
外部输入的是一个T信号，然后经过内部处理，拆分出JK信号，然后用JK触发器实现?

D到JK

由D触发器组成的其它触发器，思路都无比简单，就是让外部信号组合，组合成特征方程的样子，然后作为D信号传给D触发器即可，

就是说外部有两个接口，一个是J一个是K，分别用来实现控制对应现态量的正和反，内部就是一个D触发器，

基于D触发器的特征，D信号是什么，下个次态就是什么，所以D转换为什么触发器，都是直接让那个触发器的特征方程直接做为D信号即可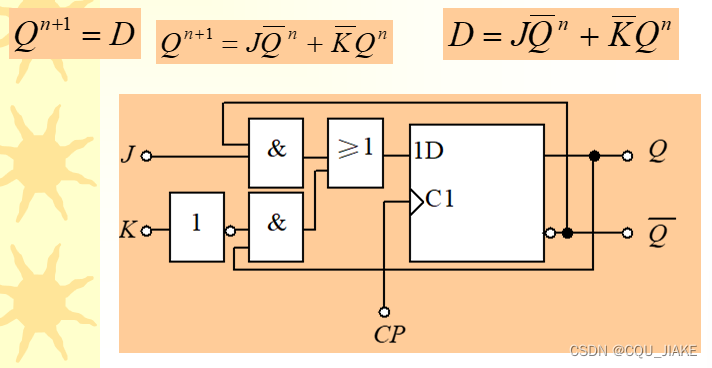

D到T

D的方程就是在下个周期设置为D，T的方程就是反转一下

所以D转换为T就是直接把现态的反接到D信号上即可

T到D

就是说外部是D触发器的接口，内部就是T触发器实现的

D触发器的方程中，与现态一点关系都没有，就是完成的D信号，就是说，外部输入一个这样的D信号，下个次态就是这个信号，由T触发器实现，就是说，在输入这样的D信号后，通过内部的一些处理，将其转换为内部T触发器可用的T信号，然后实现，就是用T触发器实现D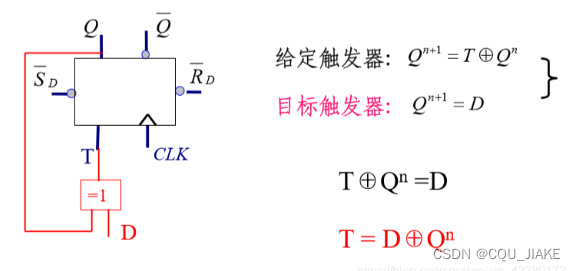

触发器设计

设计模五计数器

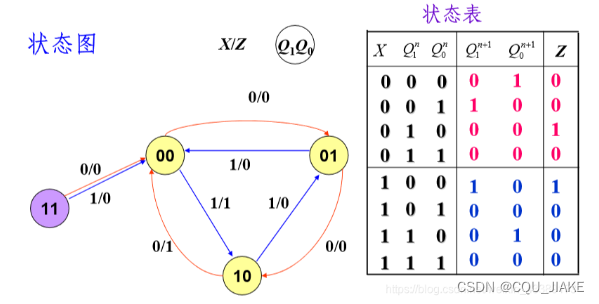
就是状态之间的转换，现态到次态，轮回变化

?

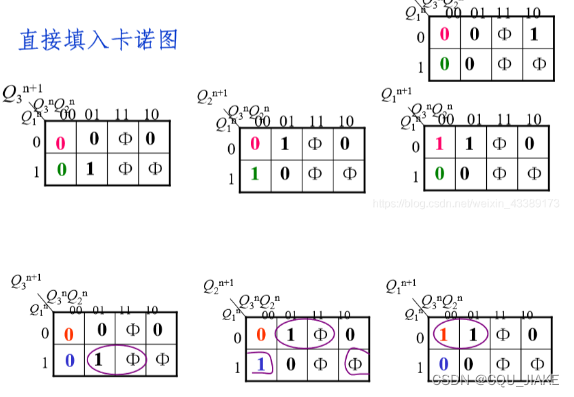这个卡诺图画的，是三个次态分量和分别的现态分量之间的关系，先得到三个式子，就是说次态分量和现态分量之间的关系，这个式子描述的是一个次态分量与三个现态分量的关系

然后接下来是选触发器

注意的是每个触发器只能确定一个状态分量，即有几个次态要确定，就要几个触发器

然后触发器方程，描绘的是次态分量与对应的现态分量之间的关系

D触发器不涉及对应的现态分量，之间全部输入即可

而其它的触发器，都要涉及到要确定的次态分量相对应的现态分量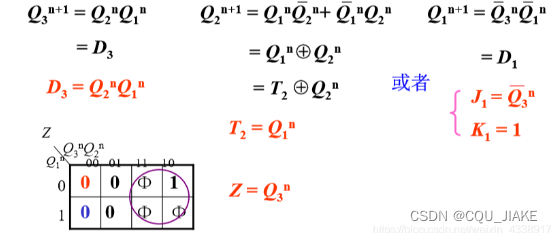

所谓触发器的相互转换，实际上就是状态方程之间的变化?

触发器特征方程，不需要考虑要确定的自己的状态分量，只需要考虑方程对应位置所需要输入的输入信号即可

思路就是先用卡诺图求出来一个次态分量与三个现态分量之间的关系，观察有没有对应的现态分量，如果没有就考虑D，有的话依据特征选触发器，有两个，一正一反的，就考虑T触发器，只有一个（正或反的），就考虑JK触发器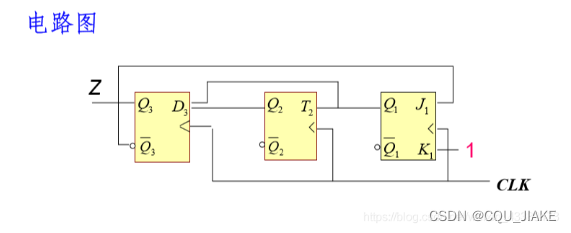

触发器的作用就是确定一个次态的状态分量?

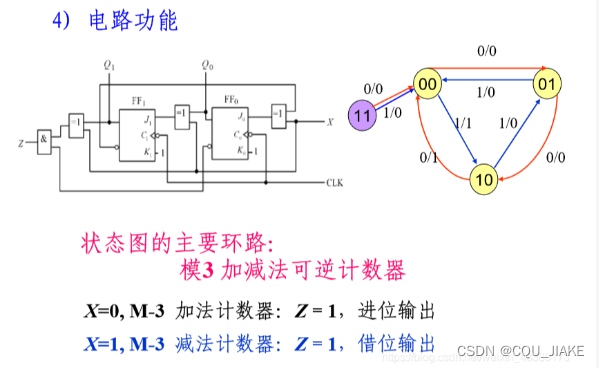
分析电路?

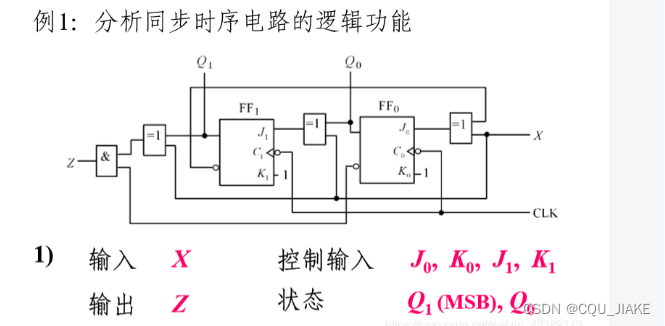
可以发现，JK触发器可以实现某个次态分量转变，转变项包含一个或两个对应的现态量，

J和K各自负责一个相应的现态分量的正反，J确定Q现态反，K确定Q现态正

就是用JK都能实现，如果不含对应的现态量的话，可以直接考虑D触发器

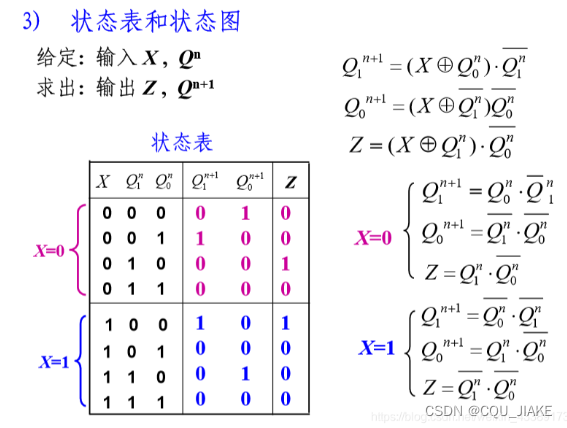
如果要逆着，去设计一个模三可逆加减计数器，先确定状态量，然后确定有几个状态分量，然后从逻辑上确定各个状态之间的转换关系，画出状态表，真值表，依据卡诺图确定各状态分量的次态与输入以及所有状态分量现态的关系，然后用触发器，最后画电路图即可

两个规则（反演与对偶）?

反演规则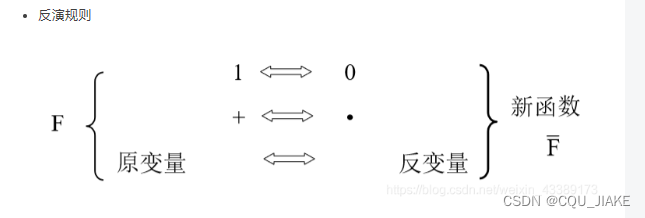

就是把常量1变为0，加变成乘，原变量取反?

对偶规则

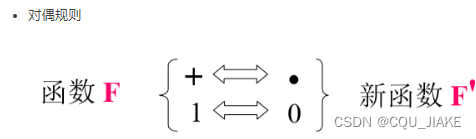
和反演唯一不一样的地方就是变量不用取反，其它都要变一下；反演是加一杠，对偶是加一撇?

有顺序问题，即先变常量，再变运算符，再变变量

反演就是在对偶的基础上，再把所有变量取一个反即可

任意两最小项之积为0，全体最小项之和为1

任意两最大项之和为1，全体最大项之积为0?

逻辑相邻就是说相邻的两个最大项/最小项，不一样的只有一个变量

卡诺图既有逻辑相邻也有几何相邻

最小项是使式子为1的取值，最大项是使式子为0的取值?

?

与或式?

1. 两种标准式间的关系

• 最大项与最小项互为反函数
• 如果不在最小项中出现的编码，一定出现在最大项的编号中。

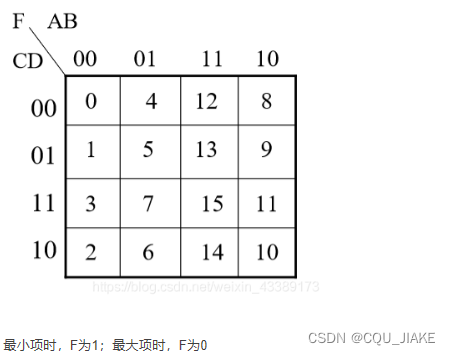
再由或与式画卡诺图时，是去标0，即哪些变量的取值可以使这个式子变为0

由与或画卡诺图时，去标1，即哪些变量的取值可以使这个式子变为1?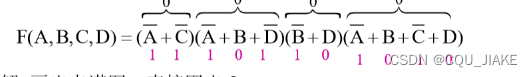

这是一个或与式，去标可以使这个式子为0的取值，?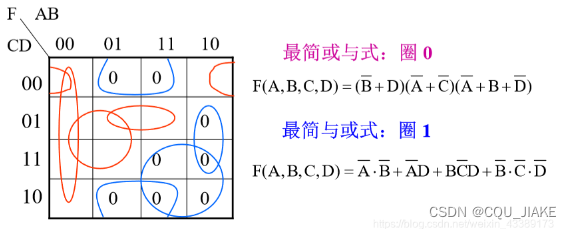

图中标的0是由原式子产生的，即使这个式子整体为0的变量取值?

然后由这个式子产出的卡诺图去找出最简式子，要画最大项，那么就是1的地方对应取反，因为目的是要让式子为0，而且找的是0

要求最小项，那么就是找1，然后1的地方就是1?

三变量表决器（组合逻辑设计电路）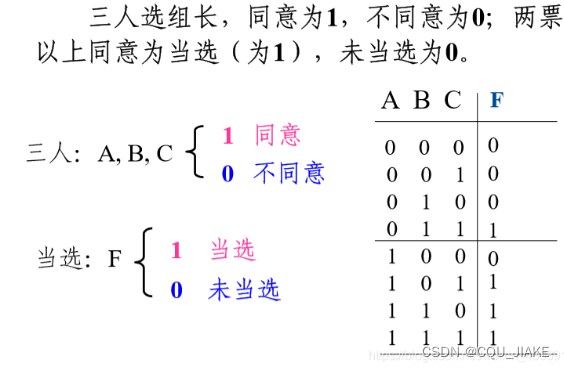

?

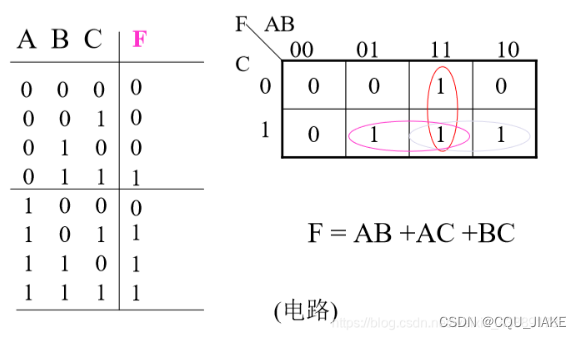没有涉及触发器，就是组合逻辑电路，输入就是模拟的所需要的情景信号输入，然后就是画真值表，依据各种输入的情况，确定输出的情况，然后画卡诺图，最后找出表达式，?

阻塞赋值与非阻塞赋值画图?

'timescale 1ns/1ns

module ex(input wire x1,

output reg f,g);

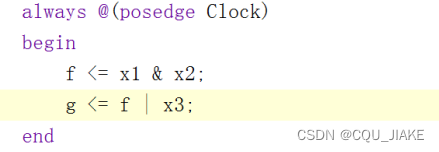
always@(posedge clk)begin

end

endmodule

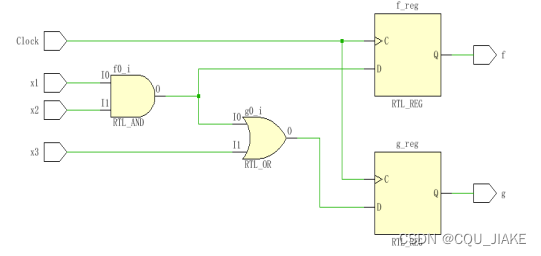
因为赋值需要时钟沿来触发，所以用了D锁存器

这里体现出阻塞，是阻塞赋值，正是因为刚才上面提到，要想确定G，就必须要先确定F，所以G的确定在F之后，即F先确定，然后G再确定，所以是阻塞

?

而如果用非阻塞，就不用等到此时的F确定，用的是上一阶段的F，这样的话G的确定就会快那么一截，即不需要等到F的确定，所以为非阻塞赋值?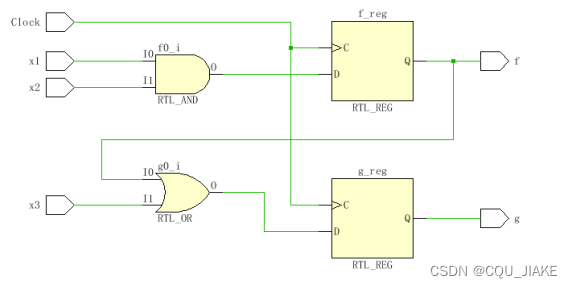

在阻塞赋值中，如果将FG的确定顺序颠倒，那就是要先确定G再确定F，那此时确定G所用的F，就不是现在阶段的F，而是上一阶段的F，即触发器存储的F，所以会生成和用非阻塞赋值一样的电路

?

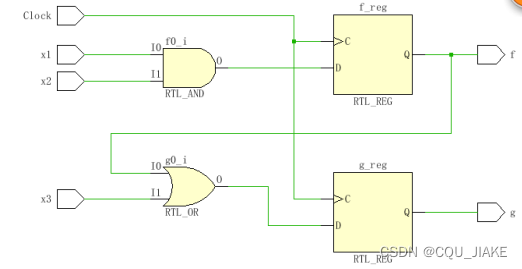而颠倒非阻塞赋值中的语句，不会产生任何影响

阻塞赋值的一个生成电路图?

?

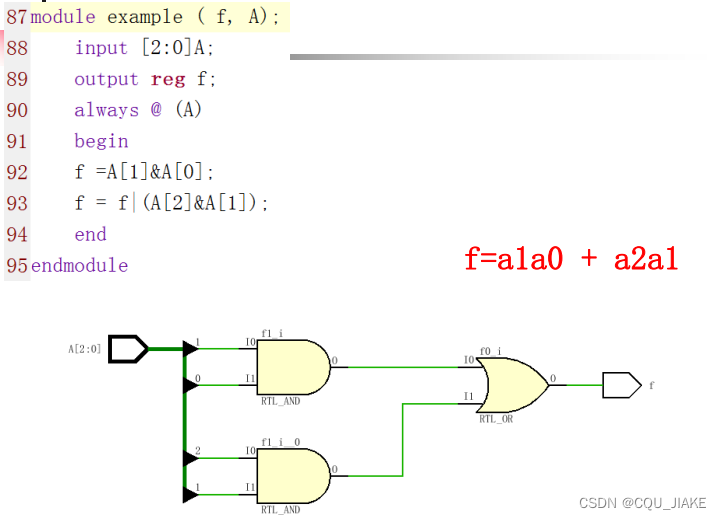如果改为非阻塞赋值?

就是说第一个语句对F产生的影响，会在下个周期才会产生影响，而第二个语句同样会对F造成影响，所以最后对F保留的是最后一条语句对F产生的影响，就对F造成了覆盖

即，如果用非阻塞的话，最后?只会保留最后一条更改的语句

?

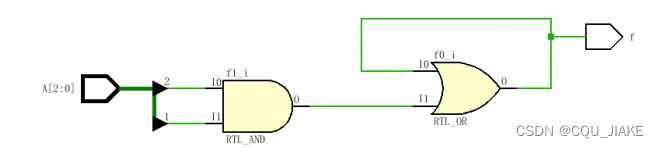后一个或门，是说最后要输出F,保存F，就是让自己再或上自己，一部分输出，一部分来或自己?

移位寄存器?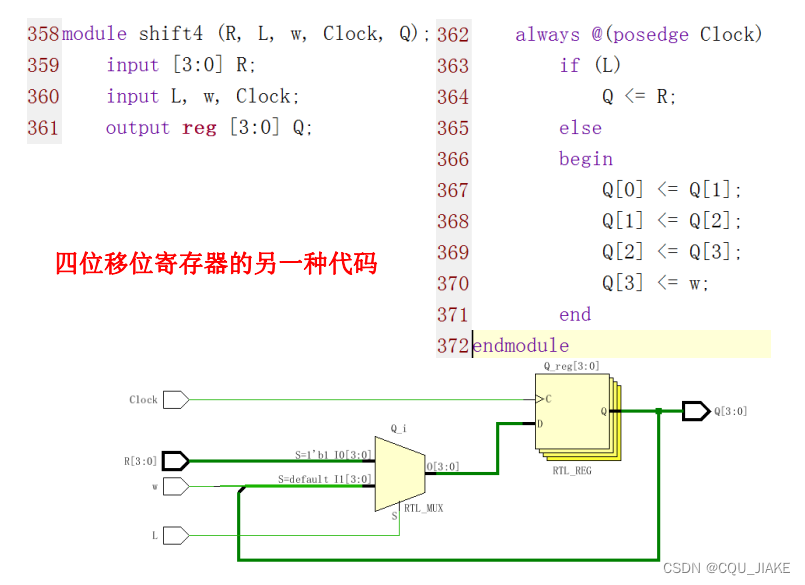

L是一个选择信号，这个寄存器叠了好几层，就是说是一个寄存器堆，确定了好几位的信号?

'timescale 1ns/1ns

modeule ff(input wire clk,

? ? ? ? ? ? ? ? input wire d,

? ? ? ? ? ? ? ? input wire rst,

? ? ? ? ? ? ? ? output reg q);

always@(posedge clk,negedge rst)begin

? ? ? ? if(!rst)

? ? ? ? ? ? ? ? q<=0;

? ? ? ? else

? ? ? ? ? ? ? ? q<=d;

end

endmodule

?

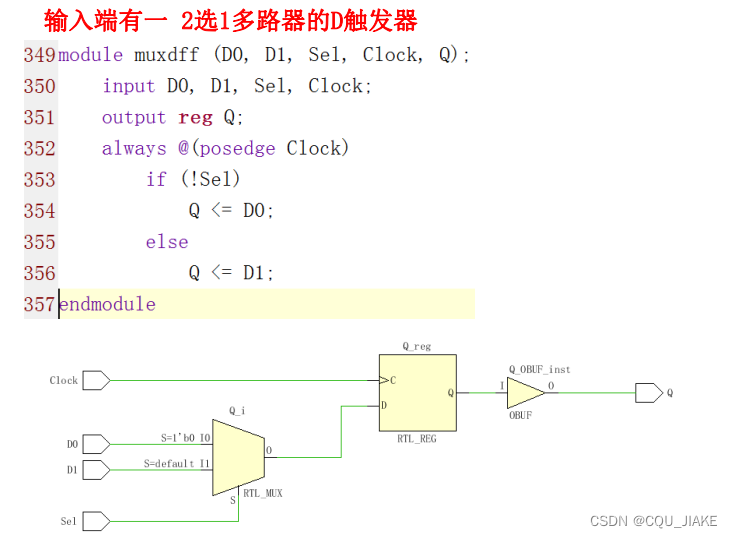
always里串行，always之间并行?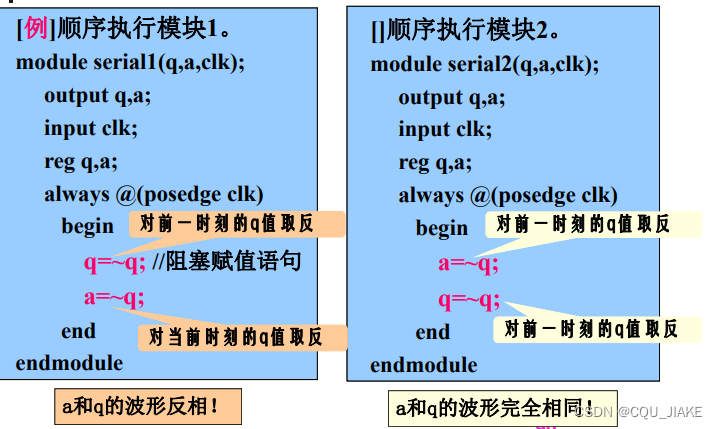

?

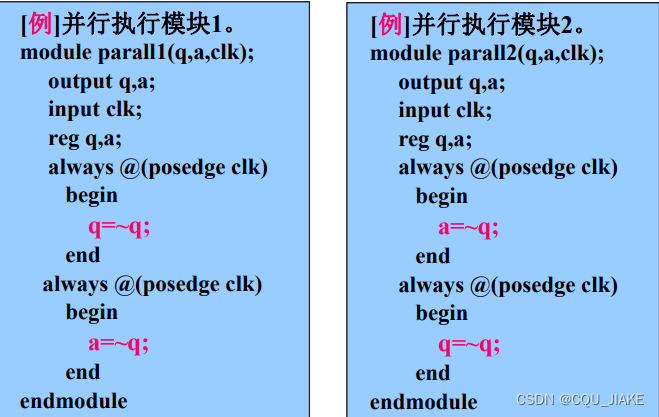在并行当中，都是对前一时刻的Q进行取反?

卡诺图的冷门性质

卡诺图的特点：在几何位置上相邻的最小项小方格在逻辑上也必定是相邻的，即相邻两项中有一个变量是互补的 。

逻辑相邻：指有且仅有一项与给出的最小项不同。两个最小项,只有一个变量的形式不同,其余的都相同。

注意是同一个变量的不同形式，即正和反

256个8位的存储器 reg[7:0]ram[0：255]?

reg [WIDTH-1:0] RAM_MEM [0:DEPTH-1];

注意前面的是数据位宽，后面的是存储器数量，前面是大的在前，后面的是大的在后面

‘timescale 1ns/1ns 前面的表示时间尺度，后面的表示时间精度，规定时间精度不能大于时间尺度e

组合逻辑因为时延不同会出现竞争和冒险?

verliog程序四大部分为，模块声明，端口定义，信号类型声明，功能描述

前面这个非阻塞，会生成两个触发器，一前一后，前面的确定B,后面的确定C,B的D信号是A,C的D信号是B

后面的就一个触发器，D信号是A，然后出来两个输出信号，一个C一个B

第一题注意或与式标的是0，圈0，然后目的是要使式子为0，要找使式子为0的变量取值，1对应的是最后表达式里的非，0对应的是正

第二题，一共四个状态，初始，1，11，111，然后用两个状态分量?

?

第一题，四位计数器，就是4位的cnt,

'timescale 1ns/1ns

module dclk(input wire clk,input wire load,input wire en,input wire rst,output reg q);

reg[3:0]cnt;

always@(posedge clk,negedge rst)begin

? ? ? ? if(!rst)

? ? ? ? ? ? ? ? cnt<=4'b0000;

? ? ? ? else begin

? ? ? ? ? ? ? ? if(en)

? ? ? ? ? ? ? ? ? ? ? ? cnt<=cnt+1'b1;

? ? ? ? ? ? ? ? else

? ? ? ? ? ? ? ? ? ? ? ? cnt<=cnt;

? ? ? ? end

end?

always@(posedge clk,negedge rst)begin

????????if(!rst)

? ? ? ? ? ? ? ? q<=0;

? ? ? ? else begin

? ? ? ? ? ? ? ? if(cnt==4'b1111)

? ? ? ? ? ? ? ? ? ? ? ? q<=1;

? ? ? ? ? ? ? ? else

? ? ? ? ? ? ? ? ? ? ? ? q<=0;

? ? ? ? end

end

endmodule

第二题，D锁存器

'timescale 1ns/1ns

module d(input clk,input rst,input d,output reg q);

always@(posedge clk,negedge rst)begin

? ? ? ? if(!rst)

? ? ? ? ? ? ? ? q<=0;

? ? ? ? else

? ? ? ? ? ? ? ? q<=d;

end

endmodule

第三题，具有同步清零的移位寄存器

'timescale 1ns/1ns

module yiwei(input clk,input rst,input d,output q);

reg[3:0]ram;

always@(posedge clk)begin

? ? ? ? if(!rst)

? ? ? ? ? ? ? ? ram<=4'b0000;

? ? ? ? else

? ? ? ? ? ? ? ? ram<={ram[2:0],d};

? ? ? ? ? ? ? ? q<=ram[3];

end

endmodule