684. Redundant Connection 685. Redundant Connection II

684. Redundant Connection

In this problem, a tree is an?undirected graph?that is connected and has no cycles.

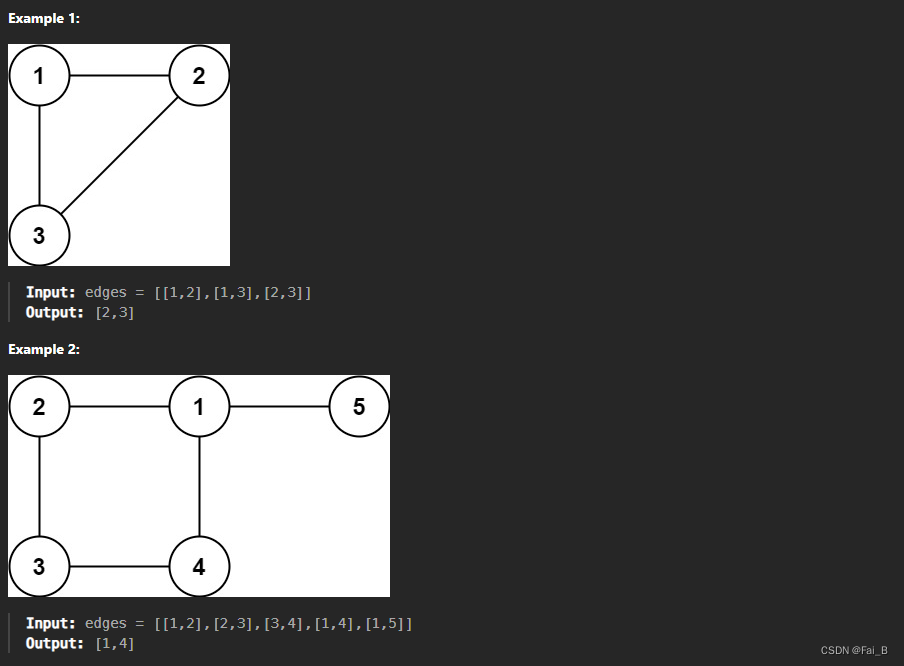
You are given a graph that started as a tree with?n?nodes labeled from?1?to?n, with one additional edge added. The added edge has two?different?vertices chosen from?1?to?n, and was not an edge that already existed. The graph is represented as an array?edges?of length?n?where?edges[i] = [ai, bi]?indicates that there is an edge between nodes?ai?and?bi?in the graph.

Return?an edge that can be removed so that the resulting剩余 graph is a tree of?n?nodes. If there are multiple answers, return the answer that occurs last in the input.

?union - find： module：

    def __init__(self):
        """
        初始化
        """
        self.n = 1005
        self.father = [i for i in range(self.n)]


    def find(self, u):
        """
        并查集里寻根的过程
        """
        if u == self.father[u]:
            return u
        self.father[u] = self.find(self.father[u])
        return self.father[u]

    def join(self, u, v):
        """
        将v->u 这条边加入并查集
        """
        u = self.find(u)
        v = self.find(v)
        if u == v : return
        self.father[v] = u
        pass


    def same(self, u, v ):
        """
        判断 u 和 v是否找到同一个根，本题用不上
        """
        u = self.find(u)
        v = self.find(v)
        return u == v

answer：

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        self.father = [i for i in range(len(edges) + 1)]
        for i in range(len(edges)):
            if self.is_same(edges[i][0], edges[i][1]): #主要逻辑，一个线段两头的father都相同这条线段就冗余redundant
                return edges[i]
            else:
                self.join(edges[i][0], edges[i][1]) #线段
        return []

    
    def find(self, u):
        if u != self.father[u]:
            self.father[u] = self.find(self.father[u])
        return self.father[u]
    
    def join(self, u, v):
        u = self.find(u)
        v = self.find(v)
        if u == v:
            return
        self.father[v] = u
        pass #可省

    def is_same(self, u, v):
        u = self.find(u)
        v = self.find(v)
        return u == v

?optimal：

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        self.father = [i for i in range(len(edges) + 1)]
        for i in range(len(edges)):
            if self.find(edges[i][0]) == self.find(edges[i][1]):
                return edges[i]
            else:
                self.father[self.find(edges[i][1])] = self.find(edges[i][0])
        return[]

    def find(self, u):
        if u != self.father[u]:
            self.father[u] = self.find(self.father[u])
        return self.father[u]

?

685. Redundant Connection II

In this problem, a rooted tree is a?directed?graph such that, there is exactly one node (the root) for which all other nodes are descendants后人?of this node, plus every node has exactly one parent, except for the root node which has no parents.

The given input is a directed graph that started as a rooted tree with?n?nodes (with distinct values from?1?to?n), with one additional directed edge added. The added edge has two different vertices chosen from?1?to?n, and was not an edge that already existed.

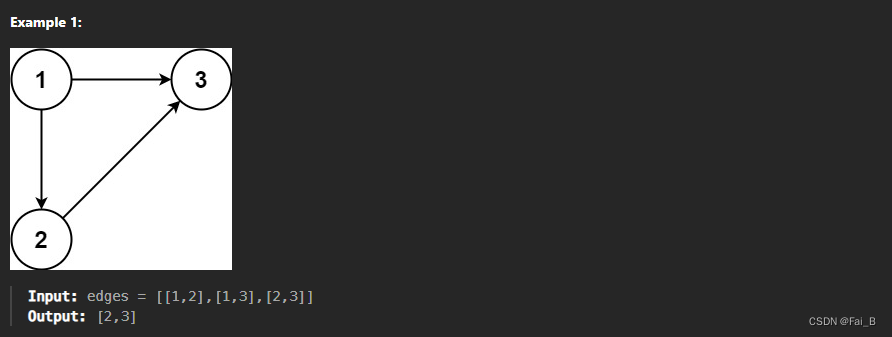
The resulting graph is given as a 2D-array of?edges. Each element of?edges?is a pair?[ui, vi]?that represents a?directed?edge connecting nodes?ui?and?vi, where?ui?is a parent of child?vi.

Return?an edge that can be removed so that the resulting graph is a rooted tree of?n?nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array.

?

?

class Solution:

    def __init__(self):
        self.n = 1010
        self.father = [i for i in range(self.n)]


    def find(self, u: int):
        """
        并查集里寻根的过程
        """
        if u == self.father[u]:
            return u
        self.father[u] = self.find(self.father[u])
        return self.father[u]

    def join(self, u: int, v: int):
        """
        将v->u 这条边加入并查集
        """
        u = self.find(u)
        v = self.find(v)
        if u == v : return
        self.father[v] = u
        pass


    def same(self, u: int, v: int ):
        """
        判断 u 和 v是否找到同一个根，本题用不上
        """
        u = self.find(u)
        v = self.find(v)
        return u == v

    def init_father(self):
        self.father = [i for i in range(self.n)]
        pass

    def getRemoveEdge(self, edges: List[List[int]]) -> List[int]:
        """
        在有向图里找到删除的那条边，使其变成树
        """

        self.init_father()
        for i in range(len(edges)):
            if self.same(edges[i][0], edges[i][1]): # 构成有向环了，就是要删除的边
                return edges[i]
            self.join(edges[i][0], edges[i][1]);
        return []

    def isTreeAfterRemoveEdge(self, edges: List[List[int]], deleteEdge: int) -> bool:
        """
        删一条边之后判断是不是树
        """

        self.init_father()
        for i in range(len(edges)):
            if i == deleteEdge: continue
            if self.same(edges[i][0], edges[i][1]): #  构成有向环了，一定不是树
                return False
            self.join(edges[i][0], edges[i][1]);
        return True

    def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
        inDegree = [0 for i in range(self.n)]

        for i in range(len(edges)):
            inDegree[ edges[i][1] ] += 1

        # 找入度为2的节点所对应的边，注意要倒序，因为优先返回最后出现在二维数组中的答案
        towDegree = []
        for i in range(len(edges))[::-1]:
            if inDegree[edges[i][1]] == 2 :
                towDegree.append(i)

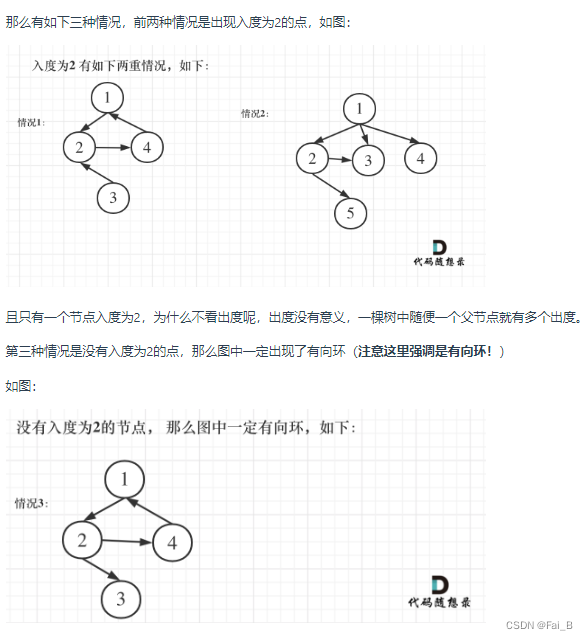
        # 处理图中情况1 和 情况2
        # 如果有入度为2的节点，那么一定是两条边里删一个，看删哪个可以构成树
        if len(towDegree) > 0:
            if(self.isTreeAfterRemoveEdge(edges, towDegree[0])) :
                return edges[towDegree[0]]
            return edges[towDegree[1]]

        # 明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了
        return self.getRemoveEdge(edges)

?