基于ADM自适应增量调制算法的matlab性能仿真

目录

1.课题概述

2.系统仿真结果

3.核心程序与模型

4.系统原理简介

4.1?ADM自适应增量调制算法简介

4.2MATLAB中实现ADM算法

5.完整工程文件

---

1.课题概述

? ? ? ?基于ADM自适应增量调制算法的matlab性能仿真，对比ADM和DM两种增量调制算法，最后输出解调后输出和参考输入之间的信噪比。

2.系统仿真结果

3.核心程序与模型

版本：MATLAB2022a

..............................................................
% 输入和预测输出比较  
figure;  
subplot(2,2,1);  
plot(t,Xref1);              % 绘制输入信号  
title('Delta调制');  
xlabel('Time(s)');  
ylabel('幅度(V)');  
hold on;  
stairs(t,DM_pred,'r');       % 绘制增量调制预测输出  
legend('Input', 'DM预测输出');  
  
% 输入和解调输出比较  
subplot(2,2,3);  
plot(t,Xref1);              % 绘制输入信号  
title('Delta解调');  
xlabel('Time(s)');  
ylabel('幅度(V)');  
hold on;  
plot(t, DM_dec,'r');       % 绘制增量解调输出  
legend('Input', 'DM解调');  
  
% ADM输入和预测输出比较  
subplot(2,2,2);  
plot(t,Xref1);              % 绘制输入信号  
title('ADM调制'); % 注意：标题应该是ADM Modulation  
xlabel('Time(s)');  
ylabel('幅度(V)');  
hold on;  
stairs(t,ADM_pred,'r');      % 绘制ADM调制预测输出  
legend('Input', 'ADM预测输出');  
  
% 输入和解调输出比较  
subplot(2,2,4);  
plot(t,Xref1);              % 绘制输入信号  
title('ADM解调'); % 注意：标题应该是ADM Modulation  
xlabel('Time(s)');  
ylabel('幅度(V)');  
hold on;  
plot(t, ADM_dec,'r');      % 绘制ADM解调输出  
legend('Input', 'ADM解调');  
  

  

SNR2  =[SNR21,SNR22];

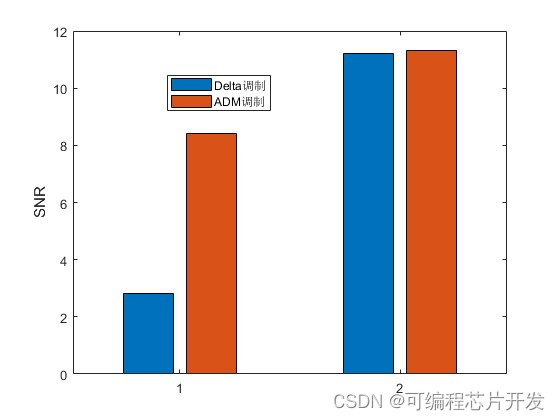
figure;
bar([SNR1;SNR2]);
ylabel('SNR');
legend('Delta调制','ADM调制');
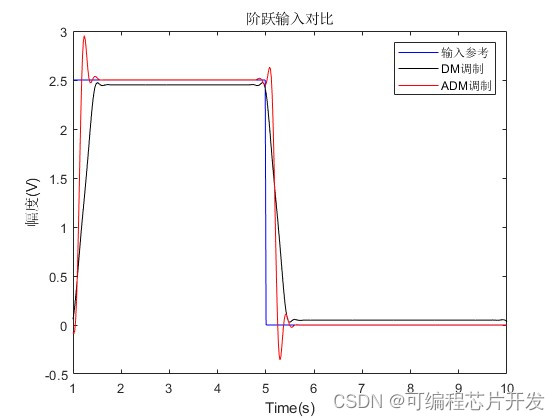
figure;  
plot(t,Xref2,'b');              % 绘制输入信号  
hold on;  
plot(t, DM_dec,'k');       % 绘制增量解调输出  
hold on;  
plot(t, ADM_dec,'r');      % 绘制ADM解调输出  
xlabel('Time(s)');  
ylabel('幅度(V)');  
legend('输入参考', 'DM调制', 'ADM调制');
title('阶跃输入对比');
20

4.系统原理简介

? ? ? ? 自适应增量调制（Adaptive Delta Modulation，ADM）是一种模拟信号到数字信号的转换技术，属于增量调制的一种改进形式。它根据输入信号的斜率变化自适应地调整量化步长，从而更有效地跟踪信号的快速变化。

4.1?ADM自适应增量调制算法简介

? ? ? ? ADM试图通过动态调整量化步长（Delta）来跟踪输入信号的斜率变化。当输入信号的斜率增加时，步长也增加；当斜率减小时，步长也减小。
工作过程：
初始化：设定初始步长Delta_0和一个预测值（通常是0）。
在每个采样时刻，计算当前采样值与预测值之差。
根据这个差值，调整预测值和可能的步长。
输出调整后的预测值作为数字化后的信号。
步长调整规则：
如果当前采样值与预测值的差超过了某个阈值（通常与步长相关），则调整预测值，并可能增加步长。
如果差值较小，则只调整预测值，并可能减小步长。

4.2MATLAB中实现ADM算法

在MATLAB中实现ADM算法，通常涉及以下步骤：

定义输入信号（如正弦波、方波等）。
初始化算法参数（如初始步长、步长调整参数等）。
实现算法逻辑，包括步长调整和预测值更新。
对输出信号进行性能评估（如计算SNR、绘制波形图等）。
?

5.完整工程文件

v

v