【低光去噪】Rethinking Noise Synthesis and Modeling in Raw Denoising

1. Motivation

• 真实原始图像噪声是由多种噪声源贡献的，并且在不同sensor之间存在差异，现有方法无论是physics-based还是leanrning-based均无法准确地建模所有的噪声源。

关于为什么无法准确地建模所有的噪声源：

2. Contribution

• 提出了一种有效和通用的噪声合成方法用于RAW域图像去噪
• 提出了raw pattern-aligned patch和high-bit reconstruction用于合成更加真实的噪声

3. Methods

3.1 建立噪声模型

对于一个典型的CMOS传感器产生的原始图像，从入射光子到输出数字信号的过程可以建模为下式：
$D$为存储在RAW图像中的数字信号， $I$为入射光子数，$N_p$为信号相关的光子散射噪声，$K_a$和$K_d$分别为模拟增益和数字增益，$N_1$和$N_2$表示在模拟增益和数字增益之前产生的其他噪声的总和。

若将噪声分解为信号相关和信号无关，则有：

重点来了，由于入射光子数是严格遵循泊松分布的，因此可以准确地合成与信号相关的光子散射噪声，只需要通过“均值-方差”的线性拟合获取总体增益即可。

对于与信号无关的噪声，作者提出了一个简单且巧妙的方法：直接从黑帧中采样。因为黑帧是在无光的条件下采集的，自然只包含了所有与信号无关的噪声。

最终合成的带噪声图像可以用下式表示：

3.2 实验及改进

作者提出的噪声合成方法过程比较简单，首先需要采集黑帧以构建数据库（默认曝光时间，每个ISO下采集10张黑帧），然后尝试采用pixel-wise的方式从黑帧中采样噪声，但是实验结果显示暗光条件下的效果不好。

作者将效果不好归因于以下两点：

• pixel-wise采样破坏了噪声的空间相关特征（如行噪声、固定模式噪声），在暗光条件下这些噪声尤为重要
• 暗光环境下信号无关噪声是主要的噪声，黑帧在ADC量化的过程中原始噪声分布被破坏

第一点比较容易解决，基于patch去采样，然后保证bayer格式对齐即可（论文中称为PAP）。例如，训练时的无噪声patch是512×512的尺寸，bayer格式为RGGB，在采样时只需要在起始行列都是偶数的限制下（保证RGGB），在黑帧中随机取出512×512的patch，然后加到干净的patch上即可。

对于第二点，作者提出了一种高比特重建（HB）的方法，将黑帧重建到更高的位宽，恢复真实的噪声分布。

为了说明高比特重建的重要性，作者对比了“P-G”与“P-G + LB”，“ELD”与“ELD + LB”的结果，“+ LB”表示将模拟的噪声量化到14bit。从Table 1中可以看出，噪声量化至14bit后，暗光图像去噪有明显的性能下降。

从消融实验的结果中可以看出，PAP和HB能够显著提升暗光图像的去噪性能。

3.3 高比特重建

高比特重建这部分看起来有些费解，但是把Figure 1看明白大概也就懂了

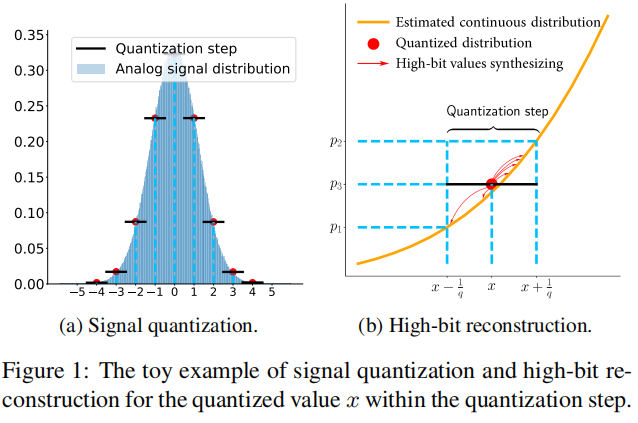
Figure 1 (a)展示了连续信号是如何量化到离散信号的，在每个量化步长范围内（黑线），连续的信号值都会被一个值代替。用数学语言描述：假设量化步长为$[x?\frac{1}{q},x+\frac{1}{q}]$，连续信号值的分布函数为$f(?)$，对于任意$a\in [x?\frac{1}{q},x+\frac{1}{q}]$，有$f(a)=c$，$c$为红点对应的纵坐标。

由于黑帧是被量化后的离散信号，也就是图中离散的红点，那么如何重建量化前的连续信号呢？Figure 1 (b)中解释的比较清楚，首先用一个分布去拟合离散的红点，也就是(b)中的黄线；然后将红点映射到采样步长$[x?\frac{1}{q},x+\frac{1}{q}]$内的任意一点（该过程用红色箭头表示），也就是将$p_3$映射到$(p_1,p_2)$范围内的某个值。

那么问题又来了，如何映射呢，总不能随机采样一个值吧~论文中是这么说的：

The sample probability of high-bit values is obtained by normalizing the estimated continuous distribution within the quantization step.
高比特值的采样概率是通过对量化步长内估计的连续分布进行归一化得到的。

这里暂时不太理解，等理解了再补充。

4. Comments

• 作者提出的噪声建模方法有点独辟蹊径的味道，抛弃了逐一分析不同噪声成分的统计分布这种复杂的物理建模，直接将噪声分解为信号相关和信号无关两部分，直接从黑帧中采样真实的信号无关噪声，正好弥补了ELD的缺陷（不能建模所有的噪声源）
• 对于高比特重建，其实从另一个角度看也是一种数据增广方式。因为采集的黑帧是有限的，而重建到高比特的过程中引入了随机性，从而增加了噪声的多样性，使得训练样本更加充足。（训练样本的多样性和充足性对于神经网络来说很重要）

Reference

Rethinking Noise Synthesis and Modeling in Raw Denoising