NNDL 作业11 LSTM [HBU ]
目录
习题6-4? 推导LSTM网络中参数的梯度, 并分析其避免梯度消失的效果
引用的博客以及文章连接:
老师博客:?【23-24 秋学期】NNDL 作业11 LSTM-CSDN博客
李宏毅机器学习笔记:RNN循环神经网络_李宏毅rnn笔记-CSDN博客
习题6-4? 推导LSTM网络中参数的梯度, 并分析其避免梯度消失的效果
强烈推荐我看的B站视频:2.前向传播的过程_哔哩哔哩_bilibili
我把这个系列来来回回听了两遍,照着UP主的思路手推了一遍,突然就感觉顿悟了。他讲的简单易懂,很细致,非常适合初学小白。
以下展示手推过程。分别是前向传播-->反向传播 梯度消失与爆炸-->如何缓解梯度消失(爆炸)。
>LSTM前向传播
先放上前向传播结论图,下图为UP主推导得出的结论:

首先介绍LSTM结构,我在平板上画了一遍,这个图中LSTM共有三个门:
??:遗忘门
??:更新门??
??:输出门
是上一时刻输入进来的Cell记忆单元,
是上一时刻输入进来的隐藏状态,
是这一时刻的输入。注意最后的输出
,有两个分支,一支作为输出(绿色支线),另一支作为下一时刻输入的隐藏状态。
为点乘,矩阵/向量对应位置相乘;
表示矩阵相加;
代表sigmoid,可以将值映射到[0,1]之间;
tanh即为tanh激活函数。

进行公式推导,先举例 推导和
:
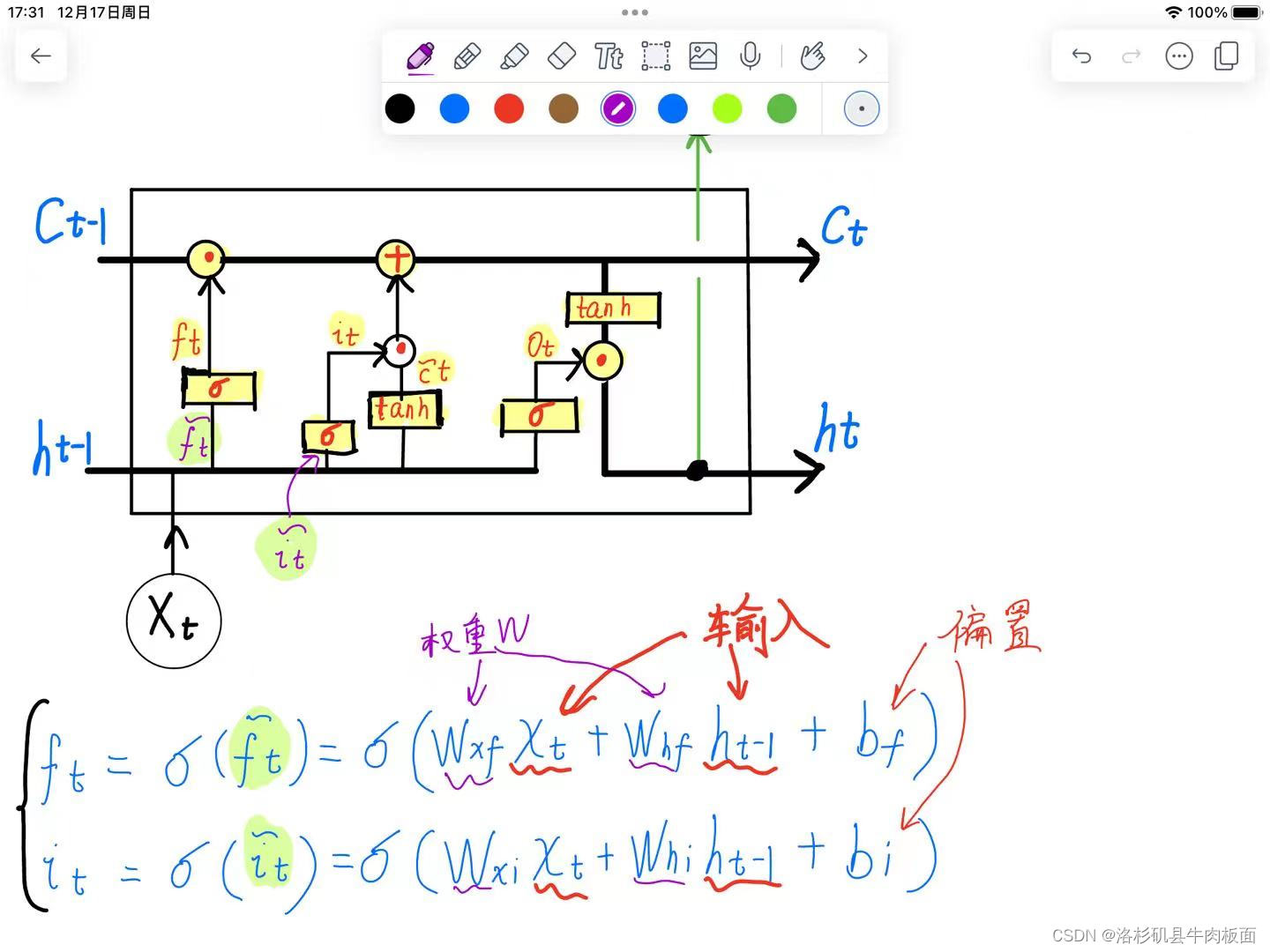
权重,输入,偏置项都已经标清楚了。sigmoid函数中的公式就是循环神经网络的前向传播公式,直接套用即可,但是一定要注意下角标,标清楚这是来自哪个门的路径角标。
以此类推,按照图中所给的结构图进行推导,照葫芦画瓢,很容易就能得到:
?
(这里使用来表示支线上的
是因为避免与记忆单元
重合,所以赋了一个新的符号)
根据路径关系,可以得到是由遗忘门和更新门进行矩阵相加得到的:
输出门:?
又因为要分出一条支路,和输出门结果做点乘,才能得到t时刻的隐藏状态
?:
其中不仅可以作为t时刻的隐藏状态,也可以作为输出
?(绿色分支的线),
的值可以根据任务需求进行设定,一般可以设:?
前向传播很好推导,就是根据现有的结构照葫芦画瓢,理清楚路径顺序和路径上的操作(比如sigmoid,tanh,点乘,相加),推出一个参数的公式来,其他参数推导公式也就大差不差了。
>反向传播 求梯度
我们以t=3 为例,三个时刻的LSTM模型结构如下图:
因为循环神经网络权重共享,所以在不同时刻 W的值都是相等的。
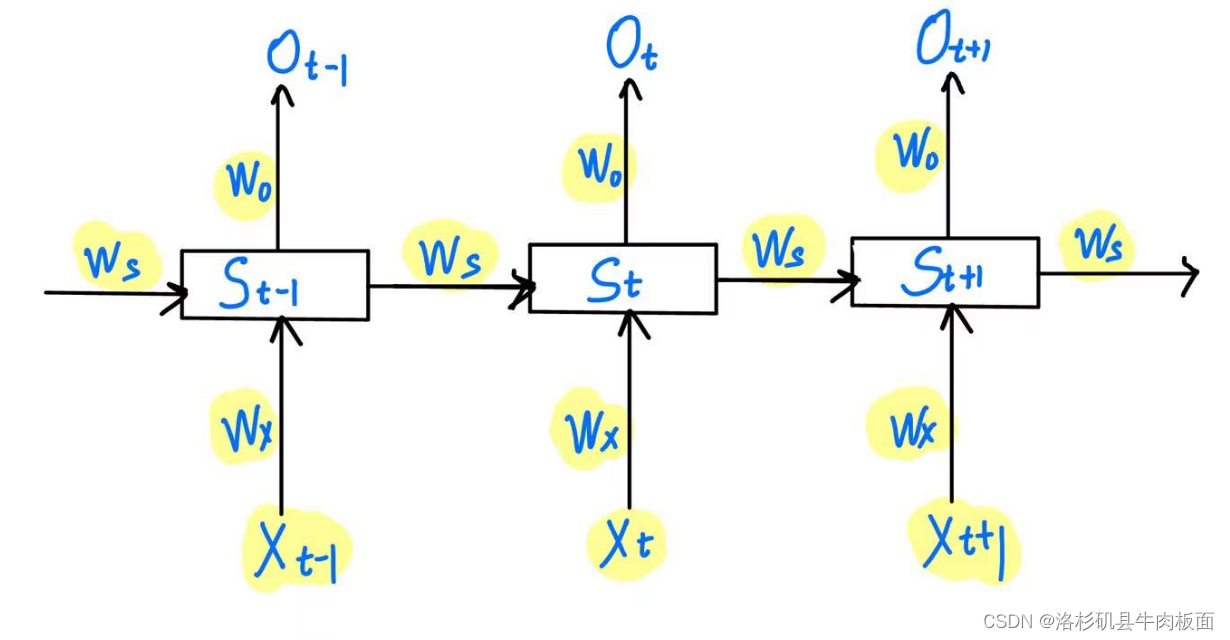
其中的表示:
预测值(输出)为为:
表示t时刻的损失Loss。当t=3时,
对
的梯度表示如下:
那么我们可以分别得到t在各个值时的链式法则求梯度公式:
?
整合一下,除了t=3时刻的式子之外,t=2 t=1时刻的式子可以提出公因式,括号内有一个连乘式?可以得到:
故对任意t时刻下,有:
即:
还有一点:应为标量,这个公式才能成立。具体原因是 公式中使用了连乘。如果
为向量,就无法满足交换律,就不能写为连乘的形式了。 这是数学上的一些细节,我资历太浅 讲不明白(捂脸),想深入探究为何的请去看一遍UP的视频。
5.LSTM如何缓解梯度消失(公式推导)_哔哩哔哩_bilibili
>梯度消失和梯度爆炸怎么来的?
原因就在于这个公式:
上面这个公式是怎么来的?---上文我写到了的表达式,截个图 放下面
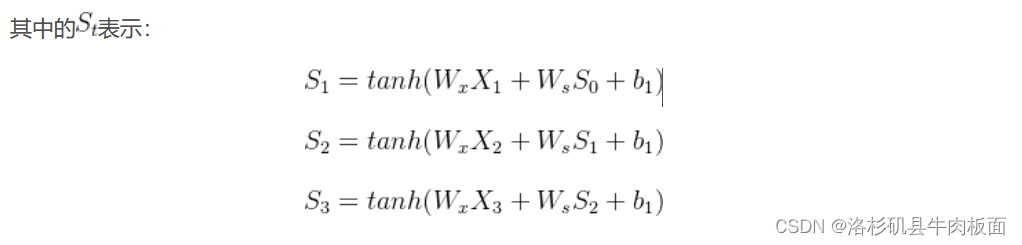
会用复合函数求导的小伙伴一眼就可以看出来,这就是求了个复合函数,才得到了这个式子。
接下来,再回顾一下刚才我们求得的链式法则梯度公式:
导致梯度爆炸和梯度消失的关键点就在于连乘,我们连乘了好多个, 而且又因为
,所以参数
的设置就至关重要了:
>如果>1,那么梯度值会越乘越大,很容易出现梯度爆炸现象。设想一下,比1大的数,经过了十几次方 或者几十次甚至几百 几千次方的连乘,这个值将变得超级大。
>如果<1,相应的,梯度值会越乘越大,就会出现梯度消失现象。W越乘越接近0,链式求导就无法进行下去了。
所以调整的值是非常关键的。
>关键点:LSTM如何缓解梯度消失?
?有了前面知识的铺垫,现在我们终于可以进入正题,那就是LSTM如何缓解梯度消失?
(看完了UP主的推导后? 被UP深深的折服了,献上了我的一键三连。)
首先我们给出结论,如下图所示:我们需要调整,使得这一项接近于1,就能缓解梯度消失现象。? ? 现在来探讨一下具体的原因。


(以上的图片为结论)
下图是我从up视频里截出来的,可见LSTM的参数非常非常多,看的人头晕。

仍然设,我们如果想求出
,就需要找到
各个时刻的梯度值。?
时刻的偏导数最好求,因为只有一条路径可以到达
;
但是时刻的偏导数就变得超级难求,因为有很多条路径可以达到
,我用平板画一画 ,大家体会一下(这一步需要对反向传播链式求导的过程很熟悉):
1. 第一条从到达
的路经(红色+绿色):
-->
-->
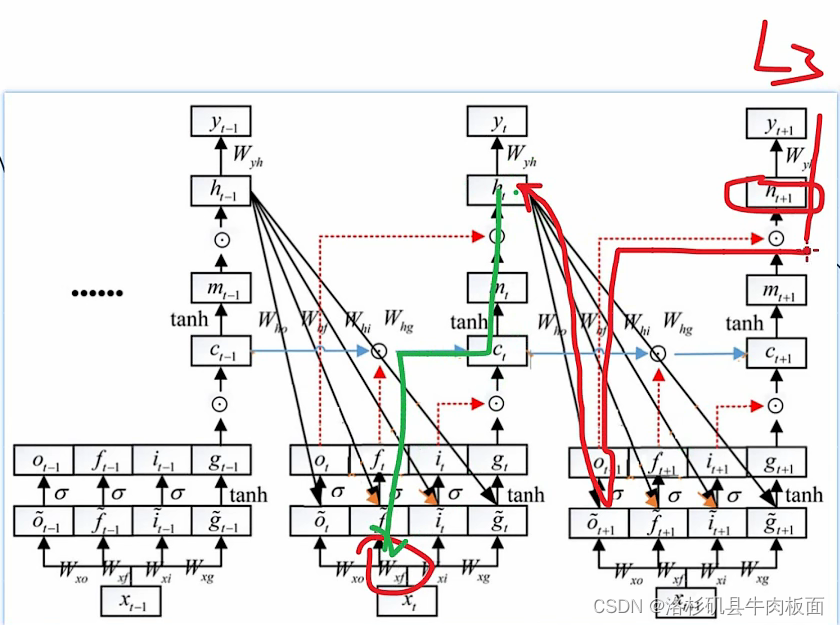
这条路径是从入手的,仔细观察红色路径的重要拐弯节点。从
可以逆推到
,再从
逆推到
。
2. 第二条从到达
的路径:

3. 第三条从到达
的路径:
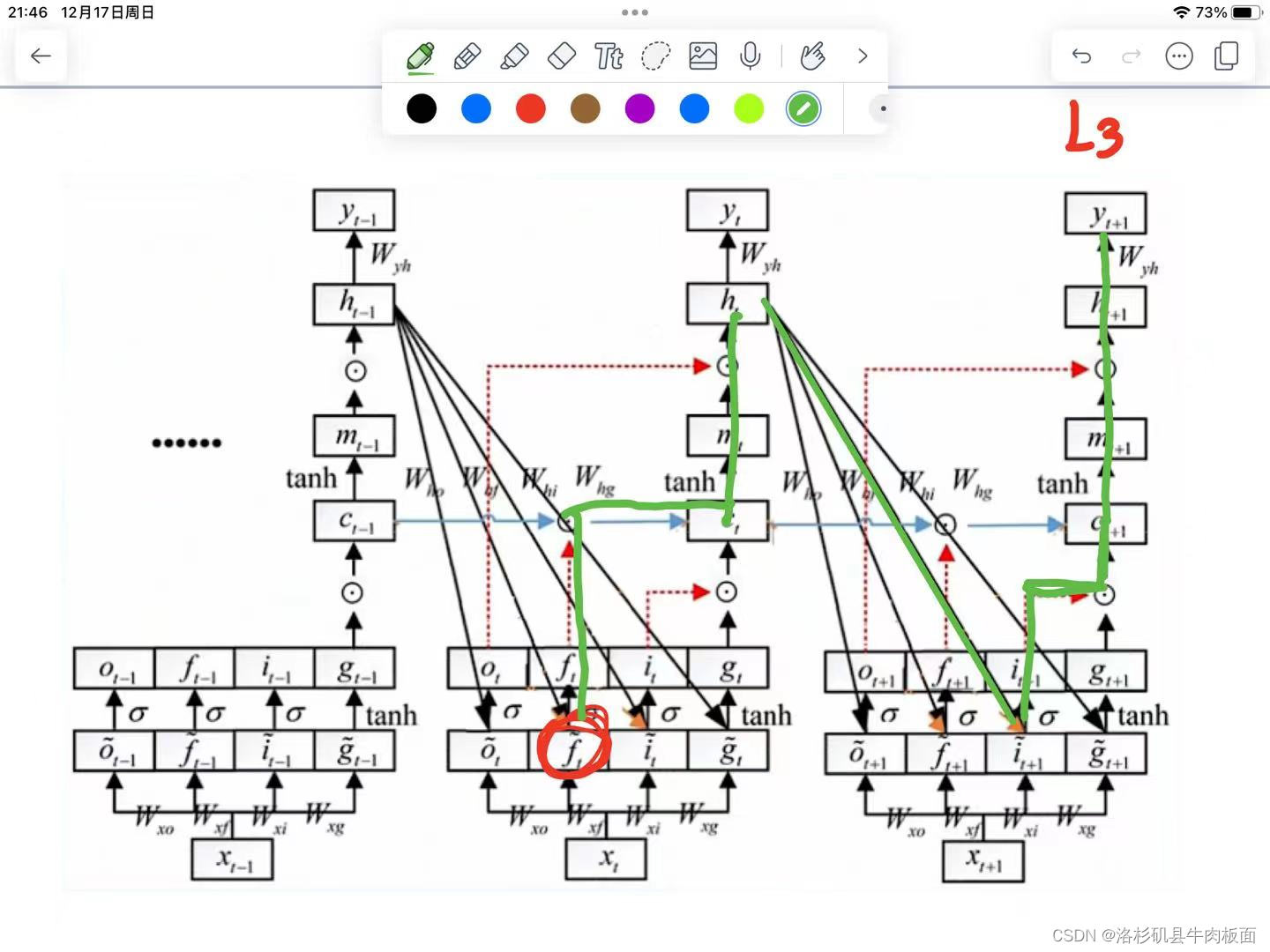
4. 第四条从到达
的路径:
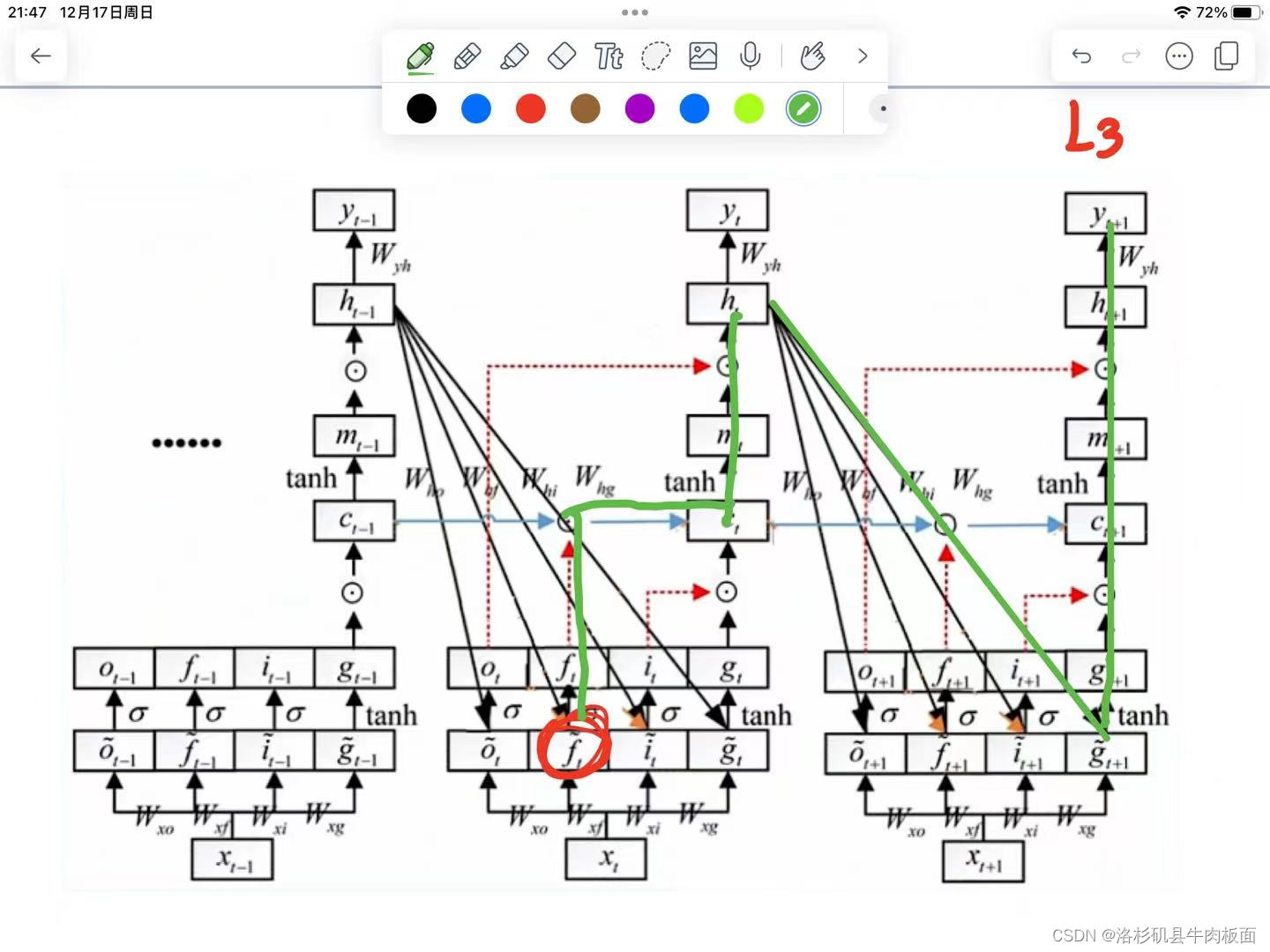
5. 第五条从到达
的路径:
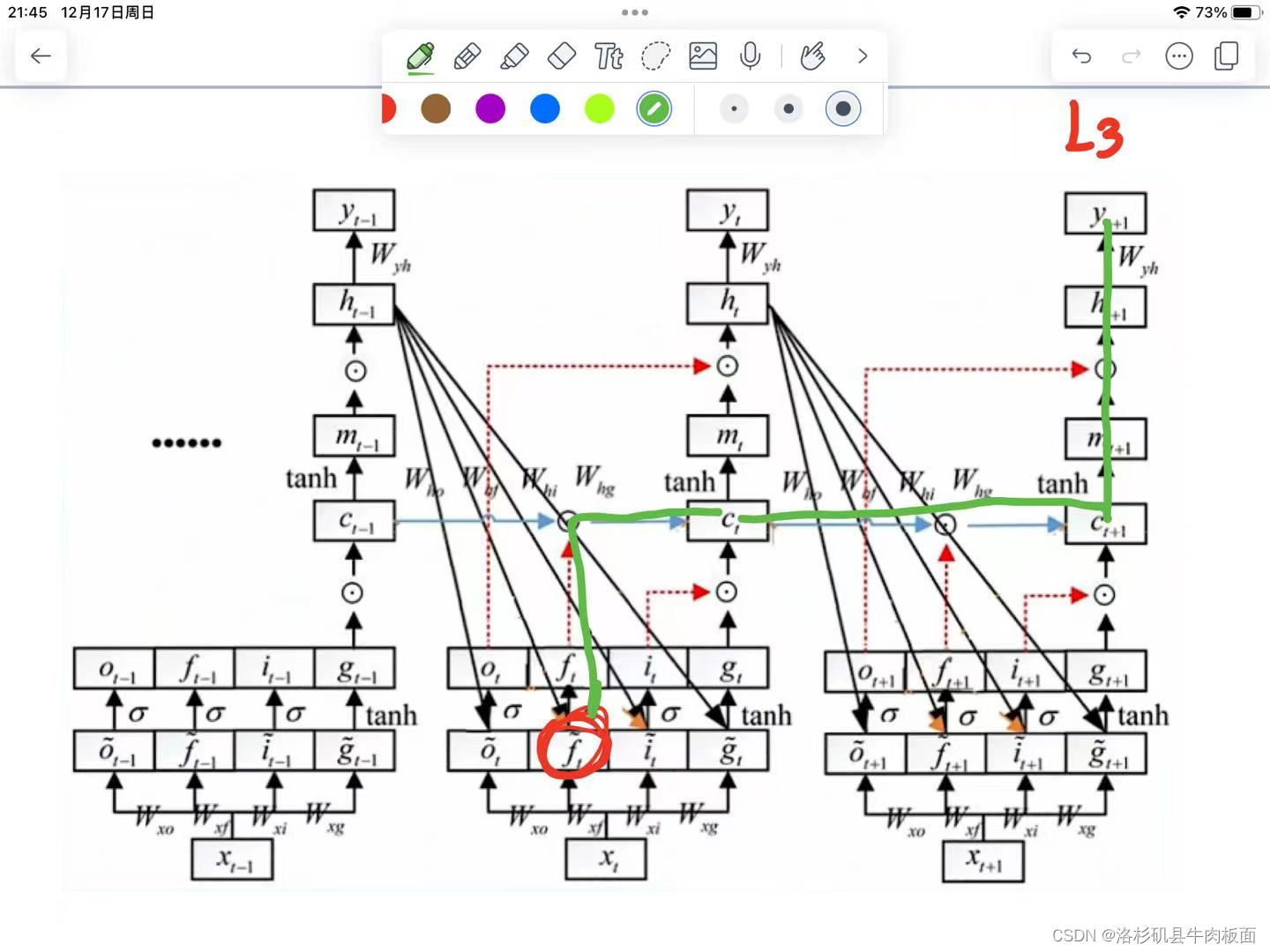
这五条路径 每一条都可以写出链式求导公式,太太太复杂了,我们理解了原理就行,公式推导无非就是换了一些角标,核心思想还是反向传播-链式求导。
这还只是时刻的链式求导公式的构建过程,
时刻的更加复杂。UP整理的
最终链式求导公式为:
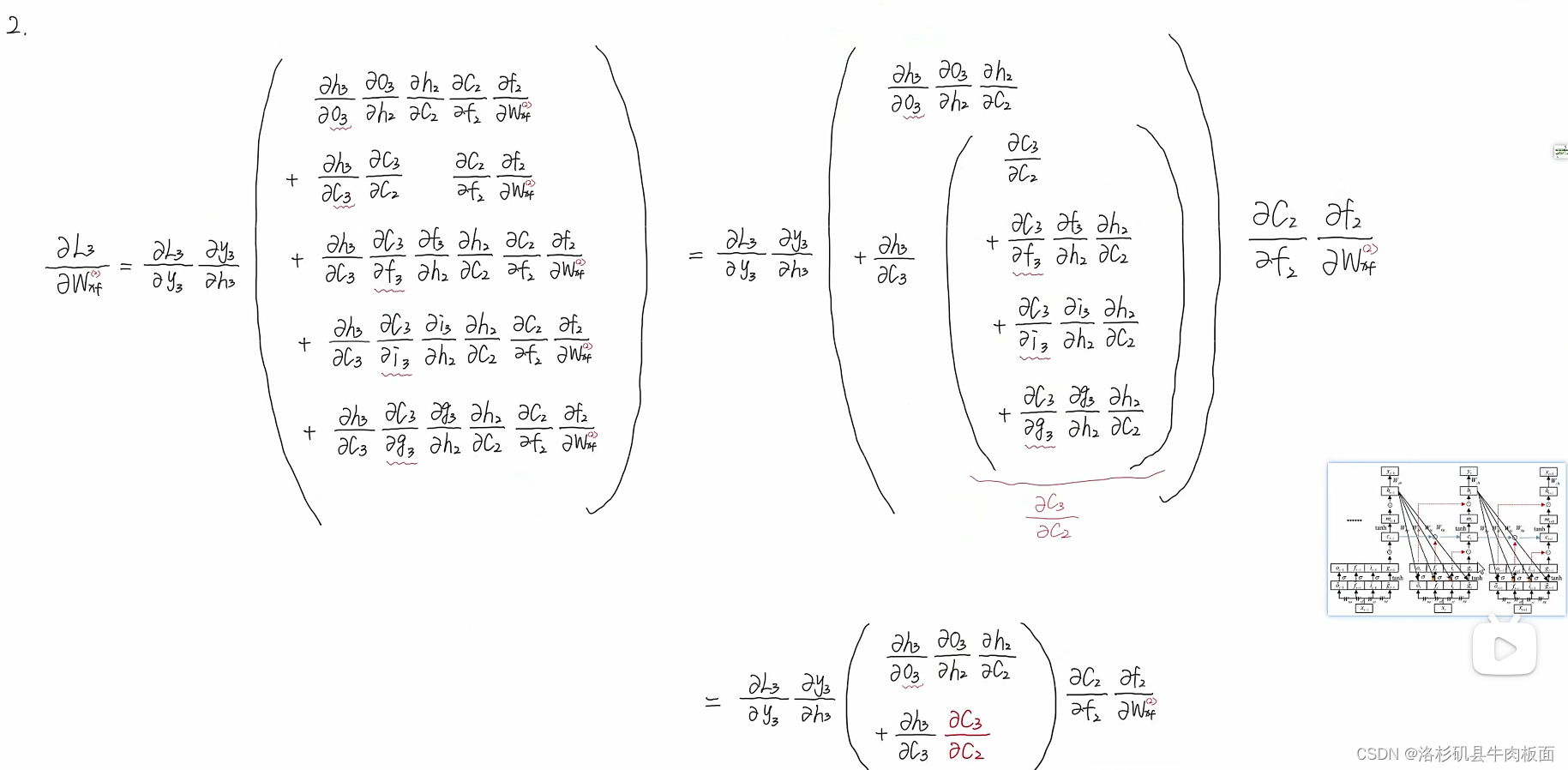
公式的关键点在这儿: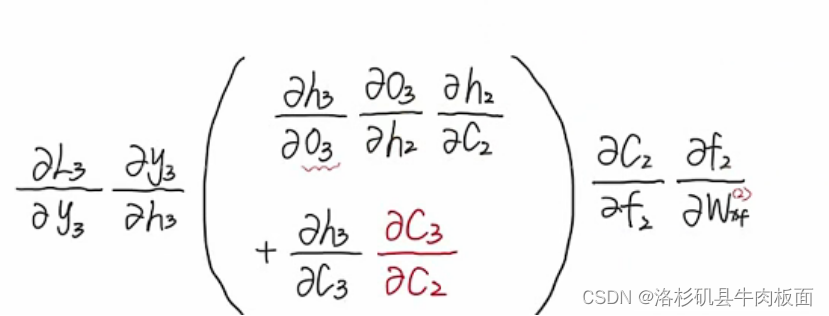
公式中的即代表着一般表达式中的
,
中集合着所有链式求导的路径,它是路径的'集合'形式。我们再回顾这个结论,结论从抽象变得具体了:

可以得到,我们需要控制W参数,使连乘项约等于多个1相乘。
这样可以同时缓解梯度消失和梯度爆炸的问题。
最后 感谢UP主的视频讲解,十分感谢UP主提供了这么详细的讲解!他的公式推导过程很详细,十分推荐大家去看他的视频。
习题6-3P??编程实现下图LSTM运行过程
1. 使用Numpy实现LSTM算子
2. 使用nn.LSTMCell实现
3. 使用nn.LSTM实现


谢谢同班同学果大神的代码思路,我在第一题里花费了好多时间,反复听了一系列课、写博客、写公式,前几天也是在一直准备英语四六级。还好有果大神的现成代码,能让我借鉴复现一下(仅管有点小小的偷懒意味,但老师说过? 学习的初始阶段就是不断地借鉴、模仿,哈哈哈 那我就借鉴一下同学写好的代码吧)
果大神博客:DL Homework 11-CSDN博客
1. 使用Numpy实现LSTM算子
代码的流程和我前文中所写的前向传播过程相匹配:
>首先赋初始值给输入和权重
>定义sigmoid函数,sigmoid函数的数学公式为
>开始循环,不断地保存上一时刻的状态,并且进行三个门的点乘运算,更新记忆细胞状态
>输出,得到结果。
代码:
#numpy算子实现LSTM
import numpy as np
#初始化输入序列,每行代表一个时间步的输入 [x1 x2 x3 label]
x = np.array([[1, 0, 0, 1],
[3, 1, 0, 1],
[2, 0, 0, 1],
[4, 1, 0, 1],
[2, 0, 0, 1],
[1, 0, 1, 1],
[3, -1, 0, 1],
[6, 1, 0, 1],
[1, 0, 1, 1]])
#权重初始化
c_W = np.array([1, 0, 0, 0]) #细胞状态权重
inputGate_W = np.array([0, 100, 0, -10])#输入门权重
outputGate_W = np.array([0, 0, 100, -10])#输出门权重
forgetGate_W = np.array([0, 100, 0, 10])#遗忘门权重
#sigmoid函数 用于LSTM中各种门的操作
def sigmoid(x):
y = 1 / (1 + np.exp(-x))
if y >= 0.5:
return 1
else:
return 0
temp = 0
y = []
c = []
for input in x:
c.append(temp) #保存上一时刻的细胞状态
temp_c = np.sum(np.multiply(input, c_W)) #新细胞状态的线性组合
#输入门 遗忘门 输出门
# multiply表示点乘运算 sigmoid将数值进行非线性变换
temp_input = sigmoid(np.sum(np.multiply(input, inputGate_W)))
temp_forget = sigmoid(np.sum(np.multiply(input, forgetGate_W)))
temp_output = sigmoid(np.sum(np.multiply(input, outputGate_W)))
temp = temp_c * temp_input + temp_forget * temp#更新细胞状态
y.append(temp_output * temp)#通过输出门得到输出,保存下来
print("Memory:", c)
print("Y :", y)结果:
2. 使用nn.LSTMCell实现
从同学那里淘来的网址,中文版pytorch网站:PyTorch - torch.nn.LSTMCell (runebook.dev)
nn.LSTMCell的使用介绍如下?:
前向传播过程
参数介绍及形状展示

权重&偏置项

使用jupyter运行一下官网给的代码:
rnn = nn.LSTMCell(10, 20) # (input_size, hidden_size)
input = torch.randn(2, 3, 10) # (time_steps, batch, input_size)
hx = torch.randn(3, 20) # (batch, hidden_size)
cx = torch.randn(3, 20)
output = []
for i in range(input.size()[0]):
hx, cx = rnn(input[i], (hx, cx))
output.append(hx)
output = torch.stack(output, dim=0)
了解了LSTMCell的基本运行原理后,开始使用LSTMCell实现所给示例:
import torch
import torch.nn as nn
#输入数据 x 维度需要变换,因为LSTMcell接收的是(time_steps,batch_size,input_size)
x = torch.tensor([[1, 0, 0, 1],
[3, 1, 0, 1],
[2, 0, 0, 1],
[4, 1, 0, 1],
[2, 0, 0, 1],
[1, 0, 1, 1],
[3, -1, 0, 1],
[6, 1, 0, 1],
[1, 0, 1, 1]], dtype=torch.float)
#增加1个batch维度,x由原来的3*4的矩阵变为3*1*4的张量
x = x.unsqueeze(1)
hidden_size=1
#使用LSTMCell定义LSTM单元
lstm_cell = nn.LSTMCell(input_size=4, hidden_size=1, bias=False)
lstm_cell.weight_ih.data = torch.tensor([[0, 100, 0, 10], # forget gate
[0, 100, 0, -10], # input gate
[1, 0, 0, 0], # output gate
[0, 0, 100, -10]]).float() #cell gate
lstm_cell.weight_hh.data = torch.zeros([4 * hidden_size, hidden_size])
# https://runebook.dev/zh/docs/pytorch/generated/torch.nn.lstmcell
#初始化隐藏状态和细胞状态 初始值设为0
hx = torch.zeros(1, hidden_size)
cx = torch.zeros(1, hidden_size)
outputs = []
for i in range(len(x)):
hx, cx = lstm_cell(x[i], (hx, cx))#前向传播
outputs.append(hx.detach().numpy()[0][0])#.detach()方法为确保tensor不计算梯度
outputs_rounded = [round(x) for x in outputs] #四舍五入到最接近的整数
print(outputs_rounded)结果:
3. 使用nn.LSTM实现
nn.LSTM相较于nn.LSTMCell增加了 num_layers
PyTorch - torch.nn.LSTM (runebook.dev)
???????
和nn.LSTMCell()的代码流程一样:
import torch
import torch.nn as nn
# 输入数据 x 维度需要变换,因为 LSTM 接收的是 (sequence_length, batch_size, input_size)
x = torch.tensor([[1, 0, 0, 1],
[3, 1, 0, 1],
[2, 0, 0, 1],
[4, 1, 0, 1],
[2, 0, 0, 1],
[1, 0, 1, 1],
[3, -1, 0, 1],
[6, 1, 0, 1],
[1, 0, 1, 1]], dtype=torch.float)
#增加1个batch维度,x由原来的3*4的矩阵变为3*1*4的张量
x = x.unsqueeze(1)
#输入size 和 隐藏状态 size
input_size = 4
hidden_size = 1
#定义LSTM模型
lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size, bias=False)
#设置权重矩阵
#只设置了输入到隐藏层的权重,而隐藏层到隐藏层的权重被设置为零。
lstm.weight_ih_l0.data = torch.tensor([[0, 100, 0, 10], # forget gate
[0, 100, 0, -10], # input gate
[1, 0, 0, 0], # output gate
[0, 0, 100, -10]]).float() # cell gate
#隐藏层到隐藏层的权重设置为零
lstm.weight_hh_l0.data = torch.zeros([4 * hidden_size, hidden_size])
#初始化隐藏状态和记忆状态
hx = torch.zeros(1, 1, hidden_size)
cx = torch.zeros(1, 1, hidden_size)
# 前向传播
outputs, (hx, cx) = lstm(x, (hx, cx))
#通过.squeeze()方法去掉batch维度,得到一个一维的输出结果
outputs = outputs.squeeze().tolist()
#四舍五入到最接近的整数
outputs_rounded = [round(x) for x in outputs]
print(outputs_rounded)结果,和使用nn.LSTMCell()构建的结果一样:
总结
这次的作业 我将主要精力都放在LSTM原理理解和公式推导部分了,选了几个B站的课程试听,最终听完了我认为讲的最详细、最适合小白听的课程,来回听了两遍。自己画了流程图,手推了前向传播过程和简单的反向传播公式。我对一下的LSTM工作流程有了更深入的了解:
前向传播-->反向传播-->梯度爆炸梯度消失问题的来源-->缓解梯度消失的方法
? ?听的最酣畅淋漓的就是梯度爆炸梯度消失问题的来源与缓解方法。原来做作业的时候,要去分析为什么神经网络模型会出现梯度爆炸和梯度消失,得到的答案就是因为? ?“权重设置不恰当,导致反向传播链式求导的时候出现了多个权值连乘 使得梯度值要么 越来越小,最终消亡 梯度接近于零 无法进行更新,要么越来越大,梯度值爆炸式的上升,使得模型更新效果大减折扣” 。原因确实是这样的,但是背后的数学原理 我还是理解得一塌糊涂,没有进行过一步步的数学公式推导,所以根本就不清楚为啥会出现“权重连乘项”。 而这次的作业,我跟着B站的课,紧跟了一遍从模型构建一直到环节梯度消失的过程 ,为什么会出现权重连乘项的问题也就迎刃而解了。
代码部分借鉴了同学们的作业,利用辅助工具(其实是文心一言)帮我理清了代码的流程,走了一遍流程,照着手敲了一遍。主要问题还是--张量的形状设置,头晕脑胀,搞不清楚...得一遍又一遍的调整形状参数。哎,我的弱项就是写代码,必须要加把劲,努力做到从头到尾原创代码。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!