三角函数倍角公式推导
1.sin(2α)=2sin(α)cos(α)
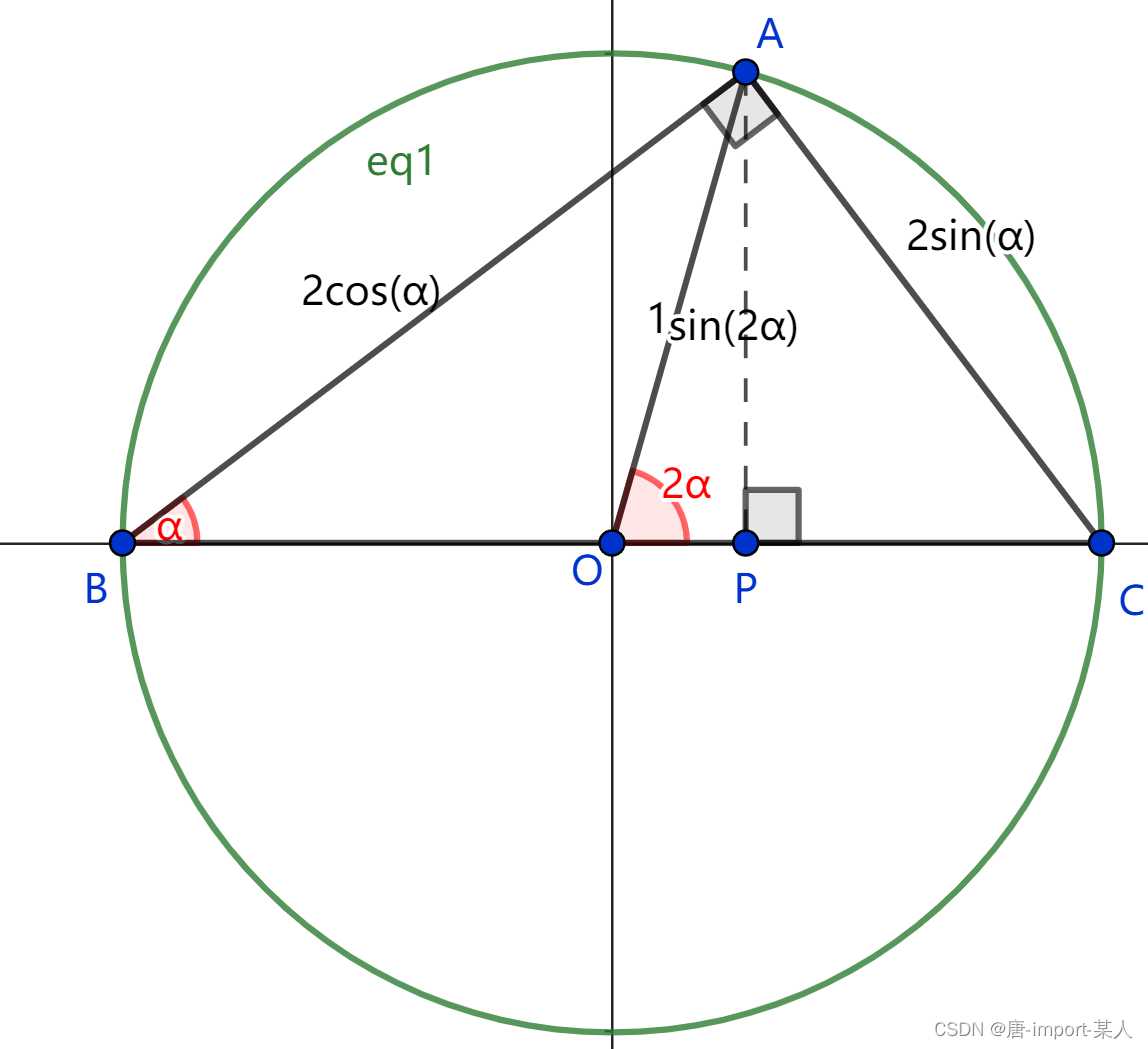
已知单位圆中有圆周三角形△ABC,圆周角为α,圆心为点O
∴
圆心角
=
2
?
圆周角
∴圆心角=2*圆周角
∴圆心角=2?圆周角
∵
∠
A
O
C
=
α
,
A
B
=
2
c
o
s
(
α
)
,
A
C
=
2
s
i
n
(
α
)
∵∠AOC=α,AB=2cos(α),AC=2sin(α)
∵∠AOC=α,AB=2cos(α),AC=2sin(α)
做
A
P
⊥
B
C
于点
P
做AP⊥BC于点P
做AP⊥BC于点P
∴
△
A
B
P
与△
A
P
O
共用边
A
P
∴△ABP与△APO共用边AP
∴△ABP与△APO共用边AP
∵
s
i
n
(
α
)
?
A
B
=
s
i
n
(
2
α
)
∵sin(α)*AB=sin(2α)
∵sin(α)?AB=sin(2α)
∵
s
i
n
(
2
α
)
=
2
s
i
n
(
α
)
c
o
s
(
α
)
∵sin(2α)=2sin(α)cos(α)
∵sin(2α)=2sin(α)cos(α)
2. c o s ( 2 α ) = c o s ( α ) 2 ? s i n ( α ) 2 cos(2α)=cos(α)^2-sin(α)^2 cos(2α)=cos(α)2?sin(α)2
∴
圆心角
=
2
?
圆周角
∴圆心角=2*圆周角
∴圆心角=2?圆周角
∵
∠
A
O
C
=
α
,
A
B
=
2
c
o
s
(
α
)
,
A
C
=
2
s
i
n
(
α
)
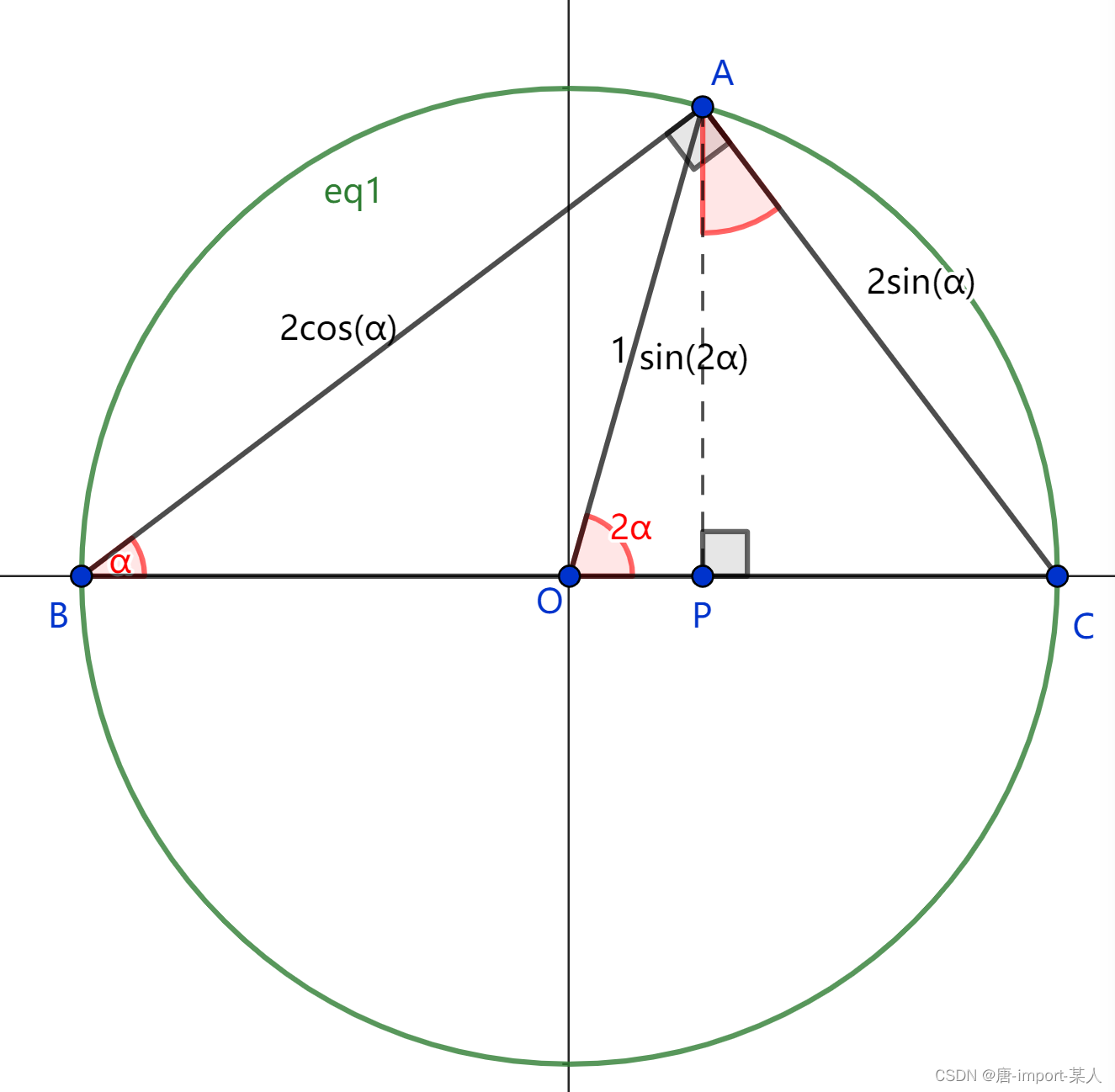
∵∠AOC=α,AB=2cos(α),AC=2sin(α)
∵∠AOC=α,AB=2cos(α),AC=2sin(α)
做
A
P
⊥
B
C
于点
P
做AP⊥BC于点P
做AP⊥BC于点P
∵
∠
P
A
C
+
∠
A
C
P
=
∠
A
B
C
+
∠
A
C
P
∵∠PAC+∠ACP=∠ABC+∠ACP
∵∠PAC+∠ACP=∠ABC+∠ACP
∵
∠
P
A
C
=
α
∵∠PAC=α
∵∠PAC=α
∵
O
P
=
1
?
2
s
i
n
(
α
)
s
i
n
(
α
)
=
c
o
s
(
2
α
)
∵OP=1-2sin(α)sin(α)=cos(2α)
∵OP=1?2sin(α)sin(α)=cos(2α)
∵
c
o
s
(
2
α
)
=
1
?
2
s
i
n
(
α
)
2
∵cos(2α)=1-2sin(α)^2
∵cos(2α)=1?2sin(α)2
∵
c
o
s
(
2
α
)
=
c
o
s
(
α
)
2
?
s
i
n
(
α
)
2
∵cos(2α)=cos(α)^2-sin(α)^2
∵cos(2α)=cos(α)2?sin(α)2
3. t a n ( 2 α ) = 2 t a n ( α ) 1 ? t a n ( α ) 2 tan(2α)=\frac{2tan(α)}{1-tan(α)^2} tan(2α)=1?tan(α)22tan(α)?
由公式1,2推tan(2α)
t
a
n
(
2
α
)
=
s
i
n
(
2
α
)
c
o
s
(
2
α
)
tan(2α)=\frac{sin(2α)}{cos(2α)}
tan(2α)=cos(2α)sin(2α)?
=
2
s
i
n
(
α
)
c
o
s
(
α
)
c
o
s
(
α
)
2
?
s
i
n
(
α
)
2
=\frac{2sin(α)cos(α)}{cos(α)^2-sin(α)^2}
=cos(α)2?sin(α)22sin(α)cos(α)?
=
2
t
a
n
(
α
)
1
?
t
a
n
(
α
)
2
=\frac{2tan(α)}{1-tan(α)^2}
=1?tan(α)22tan(α)?
4. c o t ( 2 α ) = c o t ( α ) 2 ? 1 2 c o t ( α ) cot(2α)=\frac{cot(α)^2-1}{2cot(α)} cot(2α)=2cot(α)cot(α)2?1?
由公式1,2推cot(2α)
c
o
t
(
2
α
)
=
c
o
s
(
2
α
)
s
i
n
(
2
α
)
cot(2α)=\frac{cos(2α)}{sin(2α)}
cot(2α)=sin(2α)cos(2α)?
=
c
o
s
(
α
)
2
?
s
i
n
(
α
)
2
2
s
i
n
(
α
)
c
o
s
(
α
)
=\frac{cos(α)^2-sin(α)^2}{2sin(α)cos(α)}
=2sin(α)cos(α)cos(α)2?sin(α)2?
=
c
o
t
(
α
)
2
?
1
2
c
o
t
(
α
)
=\frac{cot(α)^2-1}{2cot(α)}
=2cot(α)cot(α)2?1?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!