leetcode刷题--哈希表

题目分类 题目编号

哈希表的查找、插入及删除 217、633、349、128、202、500、290、532、205、166、466、138

哈希表与索引 1、167、599、219、220

哈希表与统计 594、350、554、609、454、18

哈希表与前缀和 560、523、525

1. 217 存在重复元素

解法一：利用unordered_map存储所有元素的出现次数，遍历map如果出现了两次以上，则返回

class Solution {
public:
       bool containsDuplicate(vector<int>& nums) {
        unordered_map<int,int>sums;
        for(auto n:nums){
            sums[n]++;
        }
        for(auto s:sums){
            if(s.second>=2)
                return true;
        }
        return false;
    }
};

时间复杂度：O(N)

空间复杂度：O(N)

解法二：由于不需要知道每个元素出现的具体次数，可以使用unordered_set来维护元素出现的次数，若将元素插入set时，发现已经在set中出现，返回true

解法三：排序，判断相邻元素是否相同。

见官方题解：217. 存在重复元素 - 力扣（LeetCode）

2. 633 平方数之和

解法一：

遍历元素i从0到sqrt?，即判断是否有整数的平方$t^2=c?i^2$。即我们令$intt=sqrt(c?i^2)$，$t$为向下取整的整数

假如$t^2==c?i^2$，说明存在返回true。否则返回false

class Solution {
public:
    bool judgeSquareSum(int c) {
        for(int i=0;i<=sqrt(c);i++){
            int tmp=c-i*i;
            int t=sqrt(tmp);
            if (t*t==tmp)
                return true;
        }
        return false;
    }
};

时间复杂度：$O（\sqrt{c}）$

空间复杂度：$O(1)$

解法二：双指针 运行速度快

由于a和b的取值范围为$[0,\sqrt{c}]$,设a<=b,初始化左指针$a=0$,右指针$b=\sqrt{c}$.

• 如果$a^2+b^2=c$,则找到相应的解，返回。
• 如果$a^2+b^2>c$,则移动右指针使其变小
• 如果$a^2+b^2<c$,则移动左指针使其变大

当a=b时，此时若没有找到整数使得$a^2+b^2=c$，则说明不存在题目要求的解。

class Solution {
public:
    bool judgeSquareSum(int c) {
        long  left=0;
        long right=sqrt(c);
        while(left<=right){
            long sum=left*left+right*right;
            if(sum==c)
                return true;
            else if(sum>c){
                right--;
            }
            else{
                left++;
            }
        }
        return false;
    }
};

为了避免sum溢出，sum必须使用long型

时间复杂度：$O（\sqrt{c}）$

空间复杂度：$O(1)$

3. 349 两个数组的交集

解法一：将nums1的元素放入set；对于nums2元素，首先排序，然后遍历nums2元素，如果相同则跳过，保证每个相同元素只判断一次是否在set中，若存在，则为其交集，假如结果集合。

class Solution {
public:
   
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        vector<int>result;
        unordered_set<int>set;
        for(auto n:nums1){
            set.insert(n);
        }
        sort(nums2.begin(),nums2.end());
        int n=nums2.size();
        int i=0;
        while(i<n){
            if(set.find(nums2[i])!=set.end()){
                result.emplace_back(nums2[i]);
            }
            while(i<n-1&&nums2[i]==nums2[i+1]){
                i++;
            }
            i++;
        }
        return result;
    }
};

解法二：排序后双指针，注意由于求的是不重复的交集，对于left和right指针指向相同元素的时候，判断其是否等于result的最后一个元素

具体见官方题解：

349. 两个数组的交集 - 力扣（LeetCode）

4. 128 最长连续序列

解法：

• 注意：这题使用到的set是unordered_set，因为其底层是哈希表实现的，可以实现常数O(1)时间的查询。

• 最常规的做法是对于每个数x，分别判断x+1,x+2…x+n是否在哈希表中，若在n+1为一个数字序列长度

• 但是这种做法也会导致$O(n^2)$的时间复杂度

• 其实观察到这个求连续序列的过程其实是重复的，即对于x+1来说，x+1…x+n为其开始的最长数字序列，但是其已经包含于x…x+n序列中，并且一定不是最长的。

• 所以我们可以通过判断x-1是否在set中来判断其是否已经在其他序列中，然后通过循环查找x+1…x+n来判断最长数字序列长度

代码：

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int>set;
        for(auto n:nums)
        set.insert(n);
        int result=0;
        for(auto n:nums){
            if(!set.count(n-1)){
                int currnum=n;
                int length=1;
                while(set.count(currnum+1)){
                    currnum++;
                    length++;
                }
                result=max(result,length);
            }
        }
        return result;
    }
};

时间复杂度：O(n)

空间复杂度：O(n)

5. 202 快乐数

解法一：

主要是平方最终会走向的可能情况的分析：

• 1.最终会得到1
• 2.最终会进入循环
• 3.值会越来越大，最后接近无穷大

情况三是否会发生？是否会继续变大？

官方中给出的解释列举了每一位数的最大数字的下一位：

对于 333 位数的数字，它不可能大于 243243243。这意味着它要么被困在 243243243 以下的循环内，要么跌到 111。444 位或 444 位以上的数字在每一步都会丢失一位，直到降到 333 位为止。所以我们知道，最坏的情况下，算法可能会在 243243243 以下的所有数字上循环，然后回到它已经到过的一个循环或者回到 111。但它不会无限期地进行下去，所以我们排除第三种选择。

快慢指针:经常使用到，在判断链表是否有环的场景下

即在找到下一个快乐数的过程中，实际上得到的是一个隐式的链表，其数据结构能形成链表结构。起始的数字是链表的头节点，链表中的其他数字都是节点。因此这个问题可以转换为链表是否有环，即使用快慢指针，慢指针移动一步，快指针移动两步，如果链表中存在环，那么快慢指针一定会相遇。

因此首先快慢指针都指向n的位置，之后每次快指针移动两步，慢指针移动一步，判断两个指针最后是否相遇，或者快指针=1。

class Solution {
public:
    int getNextHappyNum(int n){
        int sum=0;
        while(n>0){
            int d=n%10;
            n=n/10;
            sum+=d*d;
        }
        return sum;
    }
    bool isHappy(int n) {
        int lower=n;
        int faster=n;
        do{
            lower=getNextHappyNum(lower);
            faster=getNextHappyNum(getNextHappyNum(faster));
        }while(faster!=1&&lower!=faster);
        return faster==1;
    }
};

时间复杂度：O(logn)。该分析建立在对前一种方法的分析的基础上，但是这次我们需要跟踪两个指针而不是一个指针来分析，以及在它们相遇前需要绕着这个循环走多少次。
如果没有循环，那么快跑者将先到达 1，慢跑者将到达链表中的一半。我们知道最坏的情况下，成本是 O(2?log?n)=O(logn)。
一旦两个指针都在循环中，在每个循环中，快跑者将离慢跑者更近一步。一旦快跑者落后慢跑者一步，他们就会在下一步相遇。假设循环中有 k 个数字。如果他们的起点是相隔 k?1这是他们可以开始的最远的距离），那么快跑者需要k?1 步才能到达慢跑者，这对于我们的目的来说也是不变的。因此，主操作仍然在计算起始 n 的下一个值，即O(logn)。
空间复杂度：O(1)。

解法二：使用哈希表来判断链表中是否有环：但是这个哈希表比较费空间，因为需要保存所有的平方和

解法三：数学法

解法二和三见官方题解：

202. 快乐数 - 力扣（LeetCode）

6. 500 键盘行

解法：暴力解法

• 即使用三个哈希表set存储三行的元素。

• 对于words中的每个单词，首先判断单词w的首字母（通过tolower转为小写字母），判断其在哪一个set集合中

• 然后对于单词w中的其余字母判断是否也在这个集合中，若是，则加入结果集

class Solution {
public:
    vector<string> findWords(vector<string>& words) {
        vector<unordered_set<char>>maps(3);
        string line1="qwertyuiop";
        string line2="asdfghjkl" ;
        string line3="zxcvbnm" ;
        for(auto l:line1){
            maps[0].insert(l);
        }
        for(auto l:line2){
            maps[1].insert(l);
        }
        for(auto l:line3){
            maps[2].insert(l);
        }
        vector<string>result;
        for(auto w:words){
            char a=tolower(w[0]);
            int index=0;
            for(int i=0;i<maps.size();i++){
                if(maps[i].count(a)){
                    index=i;
                    break;
                }
            }
            bool flag=true;
            for(int i=1;i<w.size();i++){
                char c=tolower(w[i]);
                if(!maps[index].count(c)){
                    flag=false;
                    break;
                }
            }
            if(flag){
                result.push_back(w);
            }
        }
        return result;
    }
};

时间复杂度：O(L) L为字符串长度之和

空间复杂度：O? C是英文字母的个数

解法二：官方题解

将所有字母所在行编号，若后检测字符串中的所有字符对应的行号是否相同

500. 键盘行 - 力扣（LeetCode）

7. 290 单词规律

解法：

我们需要判断字符与字符串之间是否恰好一一对应。即任意一个字符都对应着唯一的字符串，任意一个字符串也只被唯一的一个字符对应。在集合论中，这种关系被称为「双射」。

• 本题使用两个哈希表分别表示字符到字符串的映射p2str，和字符串到字符的映射str2p。
• 然后遍历字符匹配pattern，以及按照空格切分的字符串，如果存在p2str的映射，但不存在str2p的映射，返回false；若存在str2p的映射，但是不存在p2str的映射，返回false
• 同时要注意c++没有很方便的切割字符串的方式，我们利用双指针wstart和wend找到一个单词的起始和结束位置，然后从wstart开始切割出wend-wstart个字符
• 循环的过程中若是wstart超过了s.size，说明pattern还没遍历完，但是s已经遍历完了返回false
• 最后wstart==s.size()+1,则返回true

class Solution {
public:
    bool wordPattern(string pattern, string s) {
        unordered_map<char,string>p2s;
        unordered_map<string,char>str2p;
        int m=s.size();
        int n=pattern.size();
        int wstart=0;
        int wend=0;
        for(int i=0;i<n;i++){
            if(wstart>=m){
                return false;
            }
            while(wend<m&&s[wend]!=' '){
                wend++;
            }
            string str=s.substr(wstart,wend-wstart);
            char ch=pattern[i];
            if(p2s.count(ch)&&p2s[ch]!=str){
                return false;
            }
            else if(str2p.count(str)&&str2p[str]!=ch){
                return false;
            }
            else{
                p2s[ch]=str;
                str2p[str]=ch;
            }
            wstart=wend+1;
            wend=wstart;
        }
        return wstart==(m+1);
    }
};

时间复杂度：O(n+m)，其中 n 为 pattern 的长度，m 为str 的长度。插入和查询哈希表的均摊时间复杂度均为 O(n+m)。每一个字符至多只被遍历一次。

空间复杂度：O(n+m)，其中 n 为 pattern 的长度，m 为 str 的长度。最坏情况下，我们需要存储 oattern 中的每一个字符和 str 中的每一个字符串。

8. 532 数组中的k-diff数对

解法一：set去重排序后双重循环[效率低]

• 若k=0,则用map保存重复的num个数，如果map[a]不等于0，那么解的个数加1
• 若k!=0
  • 用set先将数组去重复，得到排序后的数组
  • 双重循环找到解

代码：

class Solution {
public:
        int findPairs(vector<int>& nums, int k) {
        int result=0;
        set<int>hashset;
        vector<int>tmp_num;
       if(k==0){
            unordered_map<int,int>map;
            for(auto n:nums){
                if(map.count(n)){
                    map[n]++;
                }
                else{
                    map.emplace(n,0);
                }
            }
            for(auto it=map.begin();it!=map.end();it++){
                result+=it->second!=0?1:0;
            }
            return result;
        }
        for(auto n:nums)
            hashset.insert(n);
        int n=hashset.size();
        for(auto n:hashset)
            tmp_num.emplace_back(n);
        for(int i=0;i<n;i++){
            for(int j=n-1;j>=0;j--){
                if(tmp_num[j]-tmp_num[i]==k){
                    result++;
                    break;
                }
            }
        }
        return result;
    }
};

时间复杂度：$O(n^2)$

空间复杂度：$O（n）$

优化：实际上，k！=0可以使用map来解决

即保存每个元素出现的个数，

然后遍历map中所有key，若是map[key-k]存在，则说明有一对解，result++

优化后代码：

class Solution {
public:
  int findPairs(vector<int>& nums, int k) {
        unordered_map<int, int> mp;	// 数据的值及在数组中出现的次数
        int ans = 0;
        for (const int &num : nums) mp[num]++;	// 初始化
        for (auto & item : mp) {
            if (k == 0) {   // 如果k为0，只有当这个数出现次数 > 1 时才满足条件，并且只计算一次
                ans += mp[item.first] > 1;
            } else {   // k不同时，保证了不会计算重复数对
                ans += mp.count(item.first - k);
            }
        }
        return ans;
    }
};

时间复杂度：O(n)

空间复杂度：O(n)

解法二：排序+二分

• 先将nums数组升序排序，在第i个位置之后寻找值为nums[i]+k的元素
• 使用lower_bound函数，实际上就是二分法，判断是否存在num[j]+k这个元素，若存在，则结果加1
• 过程中需要过滤重复的元素

代码：

class Solution {
public:
    int findPairs(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end()); // 升序排列
        int n = nums.size(), ans = 0;
        for (int i = 0; i < n - 1; i++) {
            if (i > 0 && nums[i] == nums[i - 1]) continue;  // 过滤重复的数对
            auto lb = lower_bound(nums.begin() + i + 1, nums.end(), nums[i] + k);
            if (lb != nums.end() && *lb == nums[i] + k) ans++;
        }
        return ans;
    }
};

时间复杂度：O(nlongn)

空间复杂度：O(1)

解法三：排序+双指针[最快]

依次枚举左端点nums[l], 找到合适的右端点满足 nums[r] = nums[l] + k, 这里右指针每次只需要从之前的位置移动，不需要回溯。

因为l右移，一定增大，r一定只能取比上一个r更大的元素

代码：

class Solution {
public:
  int findPairs(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end()); // 升序排列
        int n = nums.size(), ans = 0;
        for (int l = 0, r = 0; l < n - 1; l++) {
            if (l > 0 && nums[l] == nums[l - 1]) continue;
          //l>=r条件，防止如1，1，3，4，5；但k=0,此时r=0必须跳过
            while (r < n && (l >= r || nums[r] < nums[l] + k)) r++;
            if (nums[l] + k == nums[r]) ans++;
        }
        return ans;
    }
};

时间复杂度：O(nlogn)

空间复杂度：O(1)

9. 205 同构字符串

解法：

需要我们判断 s 和 t 每个位置上的字符是否都一一对应，即 s 的任意一个字符被 t 中唯一的字符对应，同时 t 的任意一个字符被 s 中唯一的字符对应。这也被称为「双射」的关系。

以示例 2 为例，ttt 中的字符 a 和 r 虽然有唯一的映射 o，但对于 s 中的字符 o 来说其存在两个映射 {a,r}，故不满足条件。

因此，我们维护两张哈希表，第一张哈希表}s2t 以 s 中字符为键，映射至 t 的字符为值，第二张哈希表t2s 以 ttt 中字符为键，映射至 s 的字符为值。从左至右遍历两个字符串的字符，不断更新两张哈希表，如果出现冲突（即当前下标 index 对应的字符s[index] 已经存在映射且不为t[index] 或当前下标 index 对应的字符 t[index] 已经存在映射且不为s[index]）时说明两个字符串无法构成同构，返回false。

如果遍历结束没有出现冲突，则表明两个字符串是同构的，返回 true 即可。

代码：

class Solution {
public:
        bool isIsomorphic(string s, string t) {
        unordered_map<char,char>maps2t;
        unordered_map<char,char>mapt2s;
        int n=s.size();
        for(int i=0;i<n;i++){
            if(maps2t.count(s[i])){
                char c=maps2t[s[i]];
                if(c!=t[i]){
                    return false;
                }
            }
            if(mapt2s.count(t[i])){
                char c=mapt2s[t[i]];
                if(c!=s[i]){
                    return false;
                }
            }
            maps2t[s[i]]=t[i];
            mapt2s[t[i]]=s[i];
        }
        return true;
    }
};

时间复杂度：$O(n)$，其中 n 为字符串的长度。我们只需同时遍历一遍字符串 s 和 t 即可。
空间复杂度：$O(|\Sigma |)$，其中 $\Sigma$ 是字符串的字符集。哈希表存储字符的空间取决于字符串的字符集大小，最坏情况下每个字符均不相同，需要$O(|\Sigma |)$ 的空间。

10. 166 分数到小数

解法：模拟除法计算

首先可以明确，两个数相除要么是有限位小数，要么是无限循环小数，不可能是无限不循环小数。

• 若numerator%denominator=0,则说明结果为整数，直接返回整数的字符串类型

• 若相处为小数，则需要判断是否为循环小数，以示例3为例：

  

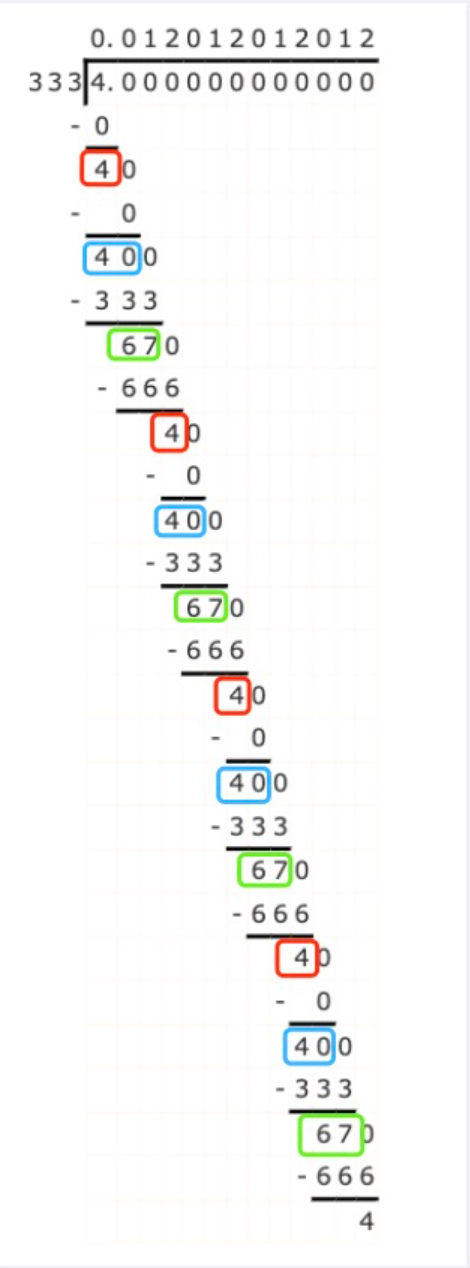
  不断的对余数进行补0操作，即成10，再重新计算余数和除数的新余数，如果当前的余数是之前出现过的余数，则说明其产生的循环小数。

• 所以我们在模拟除法的小数部分时，可是使用哈希表记录某个余数最早出现的索引位置，如果出现了相同余数，则在这个余数的第一次出现位置前加上“（”，以及当前小数字符串最后加上“)"，表示循环小数。

注意细节：

• 如果两个数字中有一个为负数，最终答案前需要加符号，然后将两个数字取绝对值
• 主要不能使用int类型表示分子和分母，因为在假设$numberator=?2^{31}和denominator=?1$的情况，结果为$2^{31}$,超出int范围了$[?2^{31},2^{31}?1]$,所以一开始应该把类型转化为Long

时间复杂度：O(l)，其中l 是答案字符串的长度，这道题中 $l\le 10^4$。对于答案字符串中的每一个字符，计算时间都是 O(1)。

空间复杂度：O(l)，其中 l 是答案字符串的长度，这道题中 $l\le 10^4$。空间复杂度主要取决于答案字符串和哈希表，哈希表中的每个键值对所对应的下标各不相同，因此键值对的数量不会超过 l。

11. 466 统计重复个数

解法：和166题类似的思路，需要找到s1中包含s2的个数，即找出循环节；

由于题目中的 n1 和 n2 都很大，因此我们无法真正把 S1 = [s1, n1] 和 S2 = [s2, n2] 都显式地表示出来。由于这两个字符串都是不断循环的，因此我们可以考虑找出 S2 在 S1 中出现的循环节，如果我们找到了循环节，那么我们就可以很快算出 S2 在 S1 中出现了多少次了。

有些读者可能对循环节这个概念会有些陌生，这个概念我们可以类比无限循环小数，如果从小数部分的某一位起向右进行到某一位止的一节数字「循环」出现，首尾衔接，称这种小数为「无限循环小数」，这一节数字称为「无限循环小数」。比如对于 3.56789789789… 这个无限循环小数，它的小数部分就是以 789 为一个「循环节」在无限循环，且开头可能会有部分不循环的部分，这个数字中即为 56。

那么回到这题，我们可以将不断循环的 s2 组成的字符串类比作上面小数部分，去找是否存在一个子串，即「循环节」，满足不断在 S2 中循环，且这个循环节能对应固定数量的 s1 。如下图所示，在第一次出现后，S2 的子串 bdadc 构成一个循环节：之后 bdadc 的每次出现都需要有相应的两段 s1。

当我们找出循环节后，我们即可知道一个循环节内包含 s1 的数量，以及在循环节出现前的 s1 的数量，这样就可以在 O(1)O(1)O(1) 的时间内，通过简单的运算求出 s2 在 S1 中出现的次数了。当然，由于 S1 中 s1 的数量 n1 是有限的，因此可能会存在循环节最后一个部分没有完全匹配，如上图最后会单独剩一个 s1 出来无法完全匹配完循环节，这部分我们需要单独拿出来遍历处理统计。

有些读者可能会怀疑循环节是否一定存在，这里我们给出的答案是肯定的，根据鸽笼原理见：抽屉原理（数学原理）_百度百科 (baidu.com)，我们最多只要找过 |s2| + 1 个 s1，就一定会出现循环节。

们设计一个哈希表cycleMap：哈希表 cycleMap 以 s2 字符串的下标 index 为索引，存储匹配至第 s1cnt 个 s1 的末尾，当前匹配到第 s2cnt 个 s2 中的第 index 个字符时， 已经匹配过的s1 的个数 s1cnt 和 s2 的个数 s2cnt 。

我们在每次遍历至 s1 的末尾时根据当前匹配到的 s2 中的位置 index 查看哈希表中的对应位置，如果哈希表中对应的位置 index 已经存储元素，则说明我们找到了循环节。循环节的长度可以用当前已经匹配的 s1 与 s2 的数量减去上次出现时经过的数量（即哈希表中存储的值）来得到。

然后我们就可以通过简单的运算求出所有构成循环节的 s2 的数量，对于不参与循环节部分的 s1，直接遍历计算即可.
上述为官方解析：https://leetcode.cn/problems/count-the-repetitions/
代码：

class Solution {
public:
        int getMaxRepetitions(string s1, int n1, string s2, int n2) {
        if(n1==0)
            return 0;
        int s1cnt=0,index=0,s2cnt=0;
        unordered_map<int,pair<int,int>>cycleMap;
        int preS1cnt,preS2cnt,cycleS1cnt,cycleS2cnt;
        do{
            ++s1cnt;
            for(char c:s1){
                if(c==s2[index])
                    index++;
                if(index==s2.size())
                {
                    s2cnt++;
                    index=0;
                }
            }
            //n1==1
            if(s1cnt==n1){
                return s2cnt/n2;
            }
            if(cycleMap.count(index)){
                //找到循环节
                preS1cnt=cycleMap[index].first;
                preS2cnt=cycleMap[index].second;
                cycleS1cnt=s1cnt-preS1cnt;
                cycleS2cnt=s2cnt-preS2cnt;
                break;
            }else{
                cycleMap[index]={s1cnt,s2cnt};
            }
        }while(1);
        //s1中包含s2的数量，根据循环节，可以通过除法计算出
        int ans=preS2cnt+(n1-preS1cnt)/cycleS1cnt*cycleS2cnt;
        int rest=(n1-preS1cnt)%cycleS1cnt;
        for(int i=0;i<rest;i++){
            for(char c:s1){
                if(c==s2[index])
                    index++;
                if(index==s2.size())
                {
                    ans++;
                    index=0;
                }
            }
        }
        return ans/n2;
    }
};

时间复杂度：O(∣s1∣×∣s2∣)。我们最多找过∣s2∣+1 个 s1，就可以找到循环节，最坏情况下需要遍历的字符数量级为O(∣s1∣×∣s2∣)。

空间复杂度：O(∣s2∣)。我们建立的哈希表大小等于 s2 的长度。

12. 138 随机链表的复制

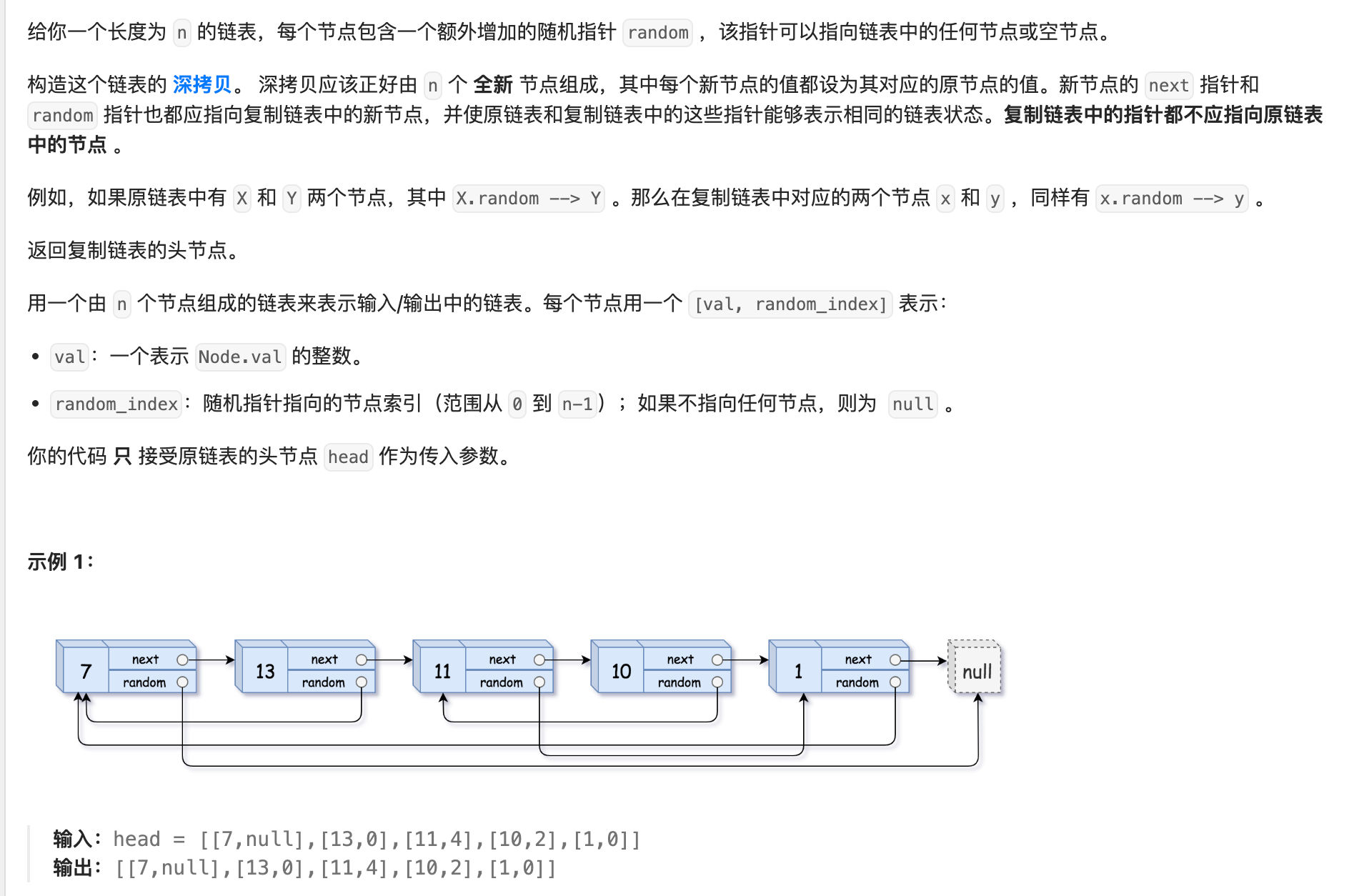
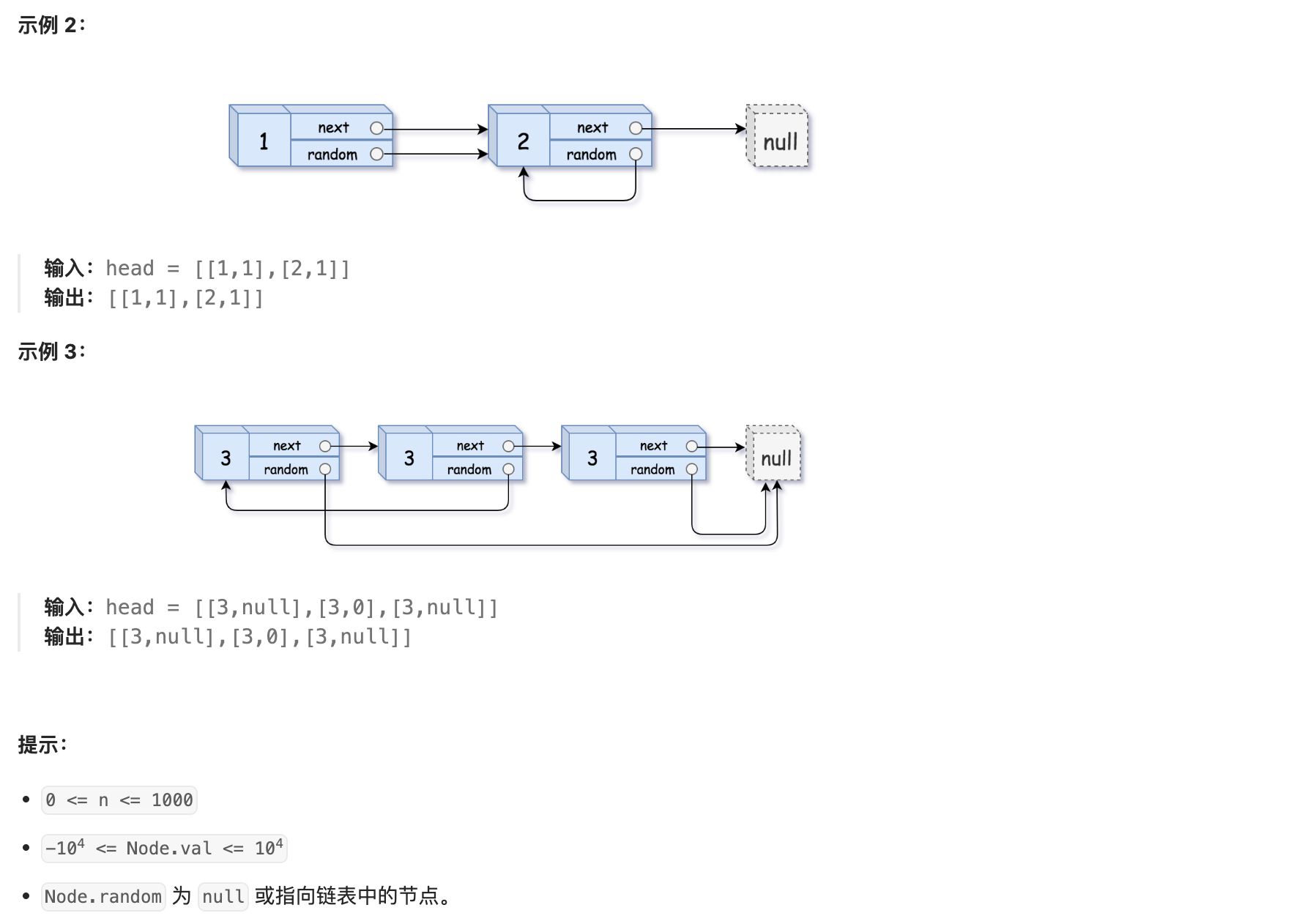
解法1:哈希表

因为单链表的复制比较简单，只需要扫描一遍。但是这个链表多了一个Random指针，有可能顺序复制的时候，Radom指针指向的位置的节点还未创建。因此，利用哈希表的查询特点，考虑构建 原链表节点 和 新链表对应节点 的键值对映射关系，提前创建好所有的复制节点，再遍历构建新链表各节点的 next 和 random 引用指向即可。

算法流程：

• 若头节点 head 为空节点，直接返回 lnull 。

• 初始化： 哈希表 map,节点 cur 指向头节点。

• 复制链表：

  • 建立新节点，并向 map添加键值对 (原 cur 节点, 新 cur 节点【为新建节点】）。

  • cur 遍历至原链表下一节点。

• 构建新链表的引用指向：

  • 构建新节点的 next 和 random 引用指向。

  • cur 遍历至原链表下一节点。

• 返回值： 新链表的头节点。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

class Solution {
public:
    Node* copyRandomList(Node* head) {
      if(head==nullptr)
      return nullptr;  
       Node*cur=head;
       Node*copyhead=new Node(cur->val);
       unordered_map<Node*,Node*>map;
       map[cur]=copyhead;
       cur=cur->next;
       while(cur!=nullptr){
           map[cur]=new Node(cur->val);
           cur=cur->next;
       }
       cur=head;
       while(cur!=nullptr){
           map[cur]->next=map[cur->next];
           map[cur]->random=map[cur->random];
           cur=cur->next;
       }
       return copyhead;
    }
};

时间复杂度 O(N) ： 两轮遍历链表，O(N) 时间。
空间复杂度 O(N) ： 哈希表 map使用线性大小的额外空间。

解法二：递归+哈希表

本题要求我们对一个特殊的链表进行深拷贝。如果是普通链表，我们可以直接按照遍历的顺序创建链表节点。而本题中因为随机指针的存在，当我们拷贝节点时，「当前节点的随机指针指向的节点」可能还没创建，因此我们需要变换思路。一个可行方案是，我们利用回溯的方式，让每个节点的拷贝操作相互独立。对于当前节点，我们首先要进行拷贝，然后我们进行「当前节点的后继节点」和「当前节点的随机指针指向的节点」拷贝，拷贝完成后将创建的新节点的指针返回，即可完成当前节点的两指针的赋值。

具体地，我们用哈希表记录每一个节点对应新节点的创建情况。遍历该链表的过程中，我们检查「当前节点的后继节点」和「当前节点的随机指针指向的节点」的创建情况。如果这两个节点中的任何一个节点的新节点没有被创建，我们都立刻递归地进行创建。当我们拷贝完成，回溯到当前层时，我们即可完成当前节点的指针赋值。注意一个节点可能被多个其他节点指向，因此我们可能递归地多次尝试拷贝某个节点，为了防止重复拷贝，我们需要首先检查当前节点是否被拷贝过，如果已经拷贝过，我们可以直接从哈希表中取出拷贝后的节点的指针并返回即可。

见官方题解：138. 随机链表的复制 - 力扣（LeetCode）

解法三：迭代+节点拆分【可以将空间复杂度降为O(1)】

见：

13. 1 两数之和

解法一：暴力双重循环，时间复杂度$O(n^2)$,空间复杂度$O(1)$不多说

解法二：哈希表

• 创建unordered_map的numsToIndex的哈希表，记录nums中的数字的值和在数组中的索引位置的映射关系
• 然后按顺序遍历数组，若在nums[target-index]在numsToIndex出现，那么说明当前已出现可以组成Target的解，直接返回两个索引位置
• 否则，记录当前的num的值和索引i的映射关系

代码：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int>numsToIndex;
        for(int i=0;i<nums.size();i++){
            int flag=numsToIndex.count(target-nums[i]);
            if(flag){
                return {numsToIndex[target-nums[i]],i};
            }
            else{
                numsToIndex[nums[i]]=i;
            }
        }
        return {};
    }
};

时间复杂度：O(N)

空间复杂度：O(N)

14. 167 两数之和II -输入有序数组

解法一：双指针

• 因为有序数组的问题，很容易想到使用双指针来解决

• 初始化时，两个指针分别指向第一个元素位置和最后一个元素的位置，并和目标值比较。

  • 如果两个元素之和等于目标值，说明发现唯一解。
  • 如果两个元素之和小小于目标值，则left指针右移一位。
  • 如果两个元素之和大于目标值，则right指针左移一位。
  • 一直重复上述操作

• 这种做法有没有可能讲唯一的解决过滤掉？不会

  证明过程：

  使用双指针的实质是缩小查找范围。那么会不会把可能的解过滤掉？答案是不会。假设 numbers[i]+numbers[j]=target。初始时两个指针分别指向下标 0 和下标numbers.length?1，左指针指向的下标小于或等于 i，右指针指向的下标大于或等于 j。除非初始时左指针和右指针已经位于下标 i和 j，否则一定是左指针先到达下标 i 的位置或者右指针先到达下标 j 的位置。

  如果左指针先到达下标 i 的位置，此时右指针还在下标 j 的右侧，sum>target，因此一定是右指针左移，左指针不可能移到 i的右侧。

  如果右指针先到达下标 j 的位置，此时左指针还在下标 i的左侧，sum<target，因此一定是左指针右移，右指针不可能移到 j 的左侧。

  由此可见，在整个移动过程中，左指针不可能移到 i 的右侧，右指针不可能移到 j 的左侧，因此不会把可能的解过滤掉。由于题目确保有唯一的答案，因此使用双指针一定可以找到答案。

代码：

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int left=0,right=numbers.size()-1;
            while(left<right){
            if(numbers[left]+numbers[right]<target)
                left++;
            else if(numbers[left]+numbers[right]>target)
                right--;
            else
                return {left+1,right+1};    
            }        
        
        return {};
    }
};

时间复杂度：O(N)

空间复杂度：O(1)

解法二：二分查找

• 遍历数组，每次固定一个数组的位置，然后从这个数字的右侧使用二分查找查找第二个数字。

  见官方题解：167. 两数之和 II - 输入有序数组 - 力扣（LeetCode）

15. 599 两个列表的最小索引总和

• 解法一：哈希表，使用一个哈希表str2index来记录list1中每个餐厅对应的索引下标，然后遍历list2，如果list2中的餐厅存在于哈希表中，那么说明该餐厅是两个人共同喜爱的，计算它们的索引和。如果该索引和比最小索引小，则清空结果，将该餐厅加入结果中，该索引和作为最小索引和；如果该索引和等于最小索引和，则直接将该餐厅加入结果中。

  小的优化：遍历list2时，如果list2的当前索引已经大于min了，则可以直接跳出循环

  代码：

  class Solution {
  public:
      vector<string> findRestaurant(vector<string>& list1, vector<string>& list2) {
          unordered_map<string,int>str2index;
          vector<string>result;
          for(int i=0;i<list1.size();i++){
              str2index[list1[i]]=i;
          }
          int min=INT_MAX;
          for(int i=0;i<list2.size();i++){
             if(i>min)
                  break;
              if(str2index.count(list2[i])){
                  int tmpMin=str2index[list2[i]]+i;
                  if(tmpMin<min){
                      min=tmpMin;
                      result.resize(0);
                      result.push_back(list2[i]);
                  }
                  else if(tmpMin==min){
                      result.push_back(list2[i]);
                  }
              }
          }
          return result;
      }
  };
  

• 时间复杂度：$O({\sum }_1+{\sum }_2)$其中 ${\sum }_1$和 ${\sum }_2$分别表示 ${list}_1$ 和 ${list}_2$ 中的字符串长度之和。建立哈希表需要 $O({\sum }_1)$，遍历 ${list}_2$需要 $O({\sum }_2)$。

  空间复杂度：$O({\sum }_1)$保存哈希表需要 $O({\sum }_1)$的空间，返回结果不计算空间复杂度。

16. 219 存在重复元素||

解法1:哈希表

• 使用hash表int2index，来记录nums中的数字和索引的映射关系，我们按顺序遍历下标i,如果在i之前存在与num[i]相等的元素，应该在这些元素中找最大的下标j，即判断$(i?j{)}_{min}$<=k。
• 因此hash表就记录每个元素的最大下标即可。从左往右遍历nums数组，进行如下操作：
  • 如果hash表中存在和num[i]相等的元素，并且该元素的下标j，满足i-j>=k,返回true;
  • 否则，将nums[i]和下标i存入hash表，是为了保证i是nums[i]的最大下标。
• 遍历结束，则没有两个相等元素的下标差的绝对值不超过k，返回false。

代码：

class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) {
        unordered_map<int,int>int2index;
        for(int i=0;i<nums.size();i++){
            if(int2index.count(nums[i])){
                int subNum=abs(int2index[nums[i]]-i);
                if(subNum<=k)
                return true;
                int2index[nums[i]]=i;
            }
            else{
                int2index[nums[i]]=i;
            }
        }
        return false;
    }
};

时间复杂度：O(n)，其中 n 是数组nums 的长度。需要遍历数组一次，对于每个元素，哈希表的操作时间都是 O(1)。

空间复杂度：O(n)，其中 n 是数组 nums 的长度。需要使用哈希表记录每个元素的最大下标，哈希表中的元素个数不会超过 n。

解法2:滑动窗口

即设置一个长度不超过k+1的滑动窗口，如果窗口内存在重复元素，一定<=k，因此只需要遍历每个滑动窗口判断是否有重复元素即可。

见官方题解：219. 存在重复元素 II - 力扣（LeetCode）

17. 220 存在重复的元素|||（hard）

解法一：hash表分桶法

分桶的方式其实类比于一个问题： 某天老师让全班同学各自说出自己的出生日期，然后统计一下出生日期相差小于等于30天的同学。我们很容易想到，出生在同一个月的同学，一定满足上面的条件。出生在相邻月的同学，也有可能满足那个条件，这就需要计算一下来确定了。但如果月份之间相差了两个月，那就不可能满足这个条件了。 例如某同学出生于6月10日，其他6月出生的同学，都与其相差小于30天。另一些5月20日和7月1日的同学也满足条件。但是4月份的和8月份的同学就不可能满足条件了。

我们按照元素的大小进行分桶，维护一个滑动窗口内的元素对应的元素。

对于元素 x，其影响的区间为 [x?t,x+t]。于是我们可以设定桶的大小为 t+1。如果两个元素同属一个桶，那么这两个元素必然符合条件。如果两个元素属于相邻桶，那么我们需要校验这两个元素是否差值不超过 t。如果两个元素既不属于同一个桶，也不属于相邻桶，那么这两个元素必然不符合条件。

具体地，我们遍历该序列，假设当前遍历到元素 x，那么我们首先检查 xxx 所属于的桶是否已经存在元素，如果存在，那么我们就找到了一对符合条件的元素，否则我们继续检查两个相邻的桶内是否存在符合条件的元素。

如果按照valueDiff的大小进行分桶，那么则分桶公式为num/valuediff，但是这样处暑不能为零，并且假设valuediff=3,数组为[0,1,2,3]，3会被分到另一个组，所以分桶的除数应该为valuediff+1；

对于负数，分桶公式应该为num+1/(valuediff+1) -1;

其详细解释见220. 存在重复元素 III - 力扣（LeetCode）

代码：

class Solution {
public:
    int getID(int x,int w){
        return x<0?(x+1)/w-1:x/w;
    }
    bool containsNearbyAlmostDuplicate(vector<int>& nums, int indexDiff, int valueDiff) {
       unordered_map<int,int>id2num;
       int n=nums.size();
       for(int i=0;i<n;i++){
           int n=nums[i];
           int id=getID(n,valueDiff+1);
           if(id2num.count(id)){
               return true;
           }
           if(id2num.count(id-1)&&abs(n-id2num[id-1])<=valueDiff){
               return true;
           }
           if(id2num.count(id+1)&&abs(n-id2num[id+1])<=valueDiff){
               return true;
           }
           id2num[id]=n;
           if(i>=indexDiff){
               id2num.erase(getID(nums[i-indexDiff],valueDiff+1));
           }
       }
       return false;
    }
};

时间复杂度：O(n)，其中 n 是给定数组的长度。每个元素至多被插入哈希表和从哈希表中删除一次，每次操作的时间复杂度均为 O(1)。

空间复杂度：O(min?(n,k))，其中 n是给定数组的长度。哈希表中至多包含 min(n,k+1) 个元素。

解法二：滑动窗口+有序集合

见题解：220. 存在重复元素 III - 力扣（LeetCode）

18. 594 最长和谐子序列

解法：哈希表

我们注意到最长和谐子序列的最大值和最小值差值为1，并且为整数数组，因此这个子序列其实只有两种元素若干个最大值和若干个最小值。

用一个哈希映射来存储每个数出现的次数，这样就能在 O(1) 的时间内得到 x 和 x+1 出现的次数。

我们首先遍历一遍数组，得到哈希映射。随后遍历哈希映射，设当前遍历到的键值对为 (x,value)，那么我们就查询 x+1 在哈希映射中对应的统计次数，就得到了 x 和 x+1 出现的次数，和谐子序列的长度等于 x 和 x+1 出现的次数之和。

class Solution {
public:
    int findLHS(vector<int>& nums) {
        unordered_map<int,int>num2count;
        int max_length=0;
        for(int num:nums){
            num2count[num]++;
        }
        for(auto it=num2count.begin();it!=num2count.end();it++){
            int num=(*it).first;
            if(num2count.find(num+1)!=num2count.end()){
                max_length=max(num2count[num]+num2count[num+1],max_length);
            }
        }
        return max_length;
    }
};

时间复杂度：O(N)，其中 N 为数组的长度。

空间复杂度：O(N)，其中 N 为数组的长度。数组中最多有 N 个不同元素，因此哈希表最多存储 N 个数据。

解法二：排序+枚举

见594. 最长和谐子序列 - 力扣（LeetCode）

19. 350 两个数组的交集II

解法1:哈希表

由于同一个数字在两个数组中都可能出现多次，因此需要用哈希表存储每个数字出现的次数。对于一个数字，其在交集中出现的次数等于该数字在两个数组中出现次数的最小值。

首先遍历第一个数组，并在哈希表中记录第一个数组中的每个数字以及对应出现的次数，然后遍历第二个数组，对于第二个数组中的每个数字，如果在哈希表中存在这个数字，则将该数字添加到答案，并减少哈希表中该数字出现的次数。

为了降低空间复杂度，首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数，然后遍历较长的数组得到交集。

class Solution {
public:
       vector<int> intersetWithSmallvector(vector<int>& nums1,vector<int>& nums2){
        unordered_map<int,int>num2count;
        vector<int>result;
        for(int n:nums1){
            num2count[n]++;
        }
        for(int n:nums2){
            if(num2count.count(n)&&num2count[n]>0){
                result.emplace_back(n);
                num2count[n]--;
            }
        }
        return result;
    }
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        if(nums1.size()>nums2.size())
            return intersetWithSmallvector(nums2,nums1);
        else
            return intersetWithSmallvector(nums1,nums2);
    }
};

时间复杂度：O(m+n)，其中 m 和 n 分别是两个数组的长度。需要遍历两个数组并对哈希表进行操作，哈希表操作的时间复杂度是 O(1)，因此总时间复杂度与两个数组的长度和呈线性关系。

空间复杂度：O(min(m,n))，其中 m 和 n 分别是两个数组的长度。对较短的数组进行哈希表的操作，哈希表的大小不会超过较短的数组的长度。为返回值创建一个数组 intersection，其长度为较短的数组的长度。

解法二：排序+双指针

见350. 两个数组的交集 II - 力扣（LeetCode）

20. 554 砖墙

解法：哈希表

由于砖墙是一面矩形，所以对于任意一条垂线，砖墙的高度是一个定值。

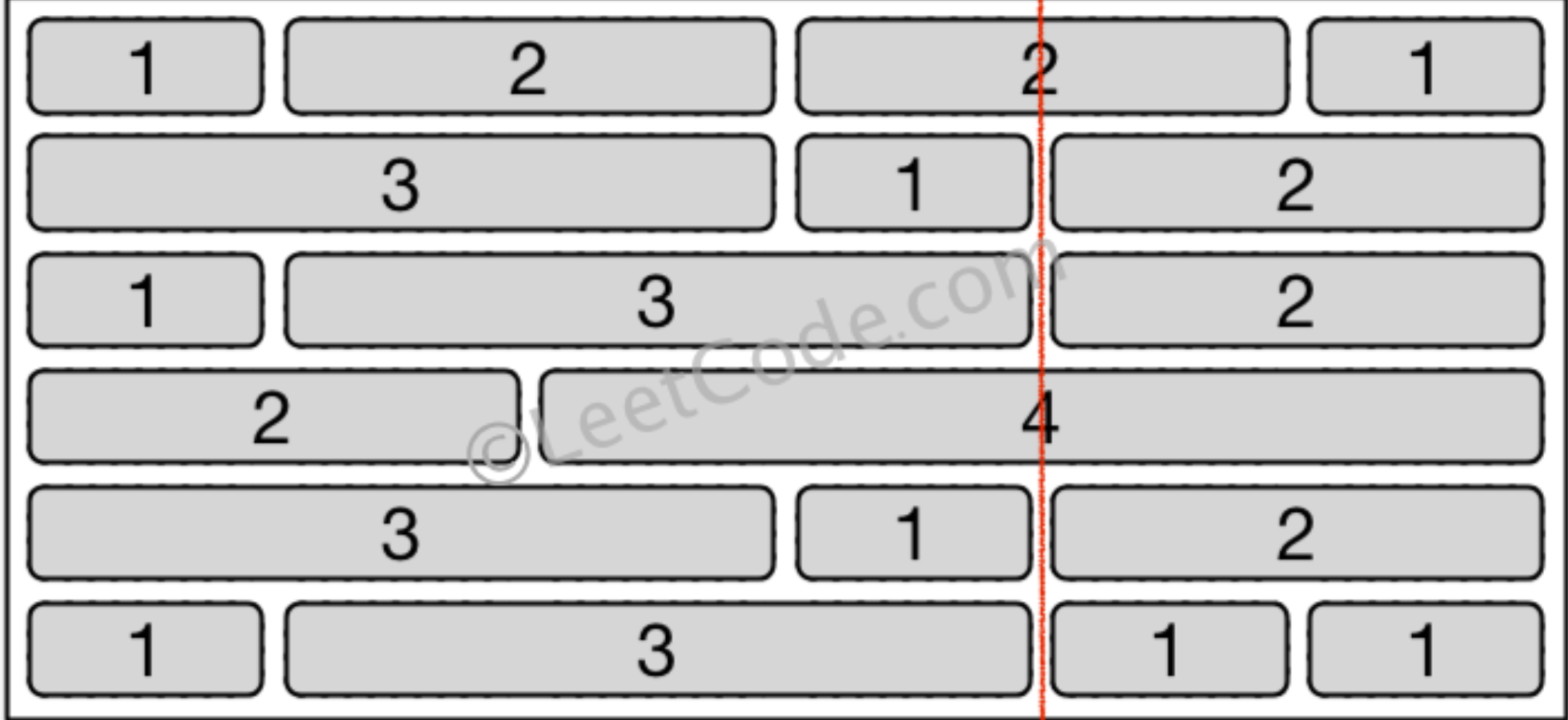
因此，问题可以转换成求：垂线穿过的砖块边缘数量的最大值，用砖墙的高度减去该最大值即为答案。

我们使用哈希表来记录每个间隙的出现次数，最终统计所有行中哪些间隙出现的最多，使用“总行数”-“间隙出现的最多次数”即可。

如下例子，发现间隙和为4的行出现了4次，次数最多。因此穿过的最少砖块数量=6-4=2

代码：

class Solution {
public:
    int leastBricks(vector<vector<int>>& wall) {
        unordered_map<int,int>nums2cnt;
        for(auto walline:wall){
            int n=walline.size();
            int sum=0;
            for(int i=0;i<n-1;i++){
                sum+=walline[i];
                nums2cnt[sum]++;
            }
        }
        int max_len=0;
        for(auto it:nums2cnt){
            int wcnt=it.second;
            max_len=max(max_len,wcnt);
        }
        return wall.size()-max_len;
    }
};

时间复杂度：O(nm)，其中 n 是砖墙的高度，m 是每行砖墙的砖的平均数量。我们需要遍历每行砖块中除了最右侧的砖块以外的每一块砖，将其右侧边缘到砖墙的左边缘的距离加入到哈希表中。

空间复杂度：O(nm)，其中 n 是砖墙的高度，m 是每行砖墙的砖的平均数量。我们需要将每行砖块中除了最右侧的砖块以外的每一块砖的右侧边缘到砖墙的左边缘的距离加入到哈希表中。

22. 454 四数相加||

• 解法：

  将四个数组分成两部分，A 和 B 为一组，C 和 D 为另外一组。

  对于 A和 B，我们使用二重循环对它们进行遍历，得到所有 A[i]+B[j] 的值并存入哈希映射中。对于哈希映射中的每个键值对，每个键表示一种 A[i]+B[j]，对应的值为 A[i]+B[j] 出现的次数。

  对于 C 和 D，我们同样使用二重循环对它们进行遍历。当遍历到 C[k]+D[l] 时，如果 ?(C[k]+D[l]) 出现在哈希映射中，那么将?(C[k]+D[l]) 对应的值累加进答案中。

  最终即可得到满足A[i]+B[j]+C[k]+D[l]=0 的四元组数目。

  class Solution {
  public:
      int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
          unordered_map<int,int>numAB;
          int ans=0;
          for(auto n1:nums1)
          for(auto n2:nums2){
              numAB[n1+n2]++;
          }
          for(auto n3:nums3)
          for(auto n4:nums4){
              if(numAB.count(-(n3+n4))){
                  ans+=numAB[-(n3+n4)];
              }
          }
          return ans;
      }
  };
  

  时间复杂度：$O(n^2)$。我们使用了两次二重循环，时间复杂度均为$O（n^2）$。在循环中对哈希表映射的修改以及查询操作的期望时间复杂度均为O（1），因此总时间复杂度为$O(n^2)$.

  空间复杂度：$O(n^2)$即为哈希映射所需要的空间。在最坏的情况下，$A[i]+B[j]$的值均不相同，因此个数为$n^2$，也就需要$O(n^2)$的空间。

23. 18 四数之和

解法：排序+双指针

排序后，枚举 nums[a] 作为第一个数，枚举nums[b] 作为第二个数，那么问题变成找到另外两个数，使得这四个数的和等于 target，这可以用双指针解决。

注意根据总和的上下界可以求出一些bound:

• 设 s=nums[a]+nums[a+1]+nums[a+2]+nums[a+3]。如果 s>target，由于数组已经排序，后面无论怎么选，选出的四个数的和不会比 s 还小，所以后面不会找到等于target 的四数之和了。所以只要 s>target，就可以直接 break 外层循环了。

• 设 s=nums[a]+nums[n?3]+nums[n?2]+nums[n?1]。如果s<target，由于数组已经排序，nums[a] 加上后面任意三个数都不会超过 s，所以无法在后面找到另外三个数与 nums[a] 相加等于 target。但是后面还有更大的 nums[a]，可能出现四数之和等于 target 的情况，所以还需要继续枚举，continue 外层循环。

• 如果 a>0 且 nums[a]=nums[a?1]，那么nums[a] 和后面数字相加的结果，必然在之前出现并且计算过，所以无需执行后续代码，直接 continue 外层循环。（可以放在循环开头判断。）

• 对于 nums[b] 的枚举（b 从 a+1 开始），也同样有类似优化：

• 设 s=nums[a]+nums[b]+nums[b+1]+nums[b+2]。如果 s>targets ，由于数组已经排序，后面无论怎么选，选出的四个数的和不会比 s 还小，所以后面不会找到等于 target 的四数之和了。所以只要 s>target，就可以直接 break。

• 设 s=nums[a]+nums[b]+nums[n?2]+nums[n?1]。如果 s<target，由于数组已经排序，nums[a]+nums[b]加上后面任意两个数都不会超过 s，所以无法在后面找到另外两个数与 nums[a] 和 nums[b] 相加等于target。但是后面还有更大的 nums[b]，可能出现四数之和等于 target\的情况，所以还需要继续枚举，continue。

• 如果 b>a+1 且 nums[b]=nums[b?1]，那么 nums[b]和后面数字相加的结果，必然在之前出现并且算出过，所以无需执行后续代码，直接 continue。

  注意：这里 b>a+1 的判断是必须的，如果不判断，对于示例 2 这样的数据，会直接 continue，漏掉符合要求的答案。

• 还需要注意的一点：非常重要

  注意到数字num[i]的取值范围为$[10^{?9},10^9]$，因此四数之和的最大可能超过int范围，因此应该选择long long 类型计算四数之和，可以将其中一个顺子转为long类型，后续相加则主动转为long类型

代码：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>>results;
        if(nums.size()<4)
        return results;
        sort(nums.begin(),nums.end());
        for(int a=0;a<=nums.size()-4;a++)
        {
            //避免得到重复的结果 
            if(a>0&&nums[a]==nums[a-1])
                continue;
            long long aBound=nums[a];    
            //如果最小的四个数都比target大，则无需遍历，说明nums[a]开头的无解，解集为空,跳出循环
            if(aBound+nums[a+1]+nums[a+2]+nums[a+3]>target)
               break;
            //如果nums[a]和最大的三个元素相加都小于target，说明nums[a]开头的无解，a需要右移，跳过   
            if(aBound+nums[nums.size()-3]+nums[nums.size()-2]+nums[nums.size()-1]<target)
                continue;   
            for(int b=a+1;b<=nums.size()-3;b++){
                if(b>a+1&&nums[b]==nums[b-1])
                    continue;
                long long bBound=nums[b]; 
             //同理如果nums[a]和nums[b]和最小的两个数字相加都大于target，则无需遍历，以nums[a],nums[b]开头的无解，跳出循环
                if(aBound+bBound+nums[b+1]+nums[b+2]>target)
                break;
             //nums[a]和nums[b]和最大的两个数字相加都小于target，则以nums[a],nums[b]开头的无解，b需要右移
                if(aBound+bBound+nums[nums.size()-2]+nums[nums.size()-1]<target)
                continue;
                int left=b+1;
                int right=nums.size()-1;
                while(left<right){
                    long long  sum=aBound+bBound+nums[left]+nums[right];
                    if(sum==target){
                        results.push_back({nums[a],nums[b],nums[left],nums[right]});
                         while(left<right&&nums[left]==nums[left+1]){
                        left++;
                    }
                    left++;
                   while(left<right&&nums[right]==nums[right-1]){
                        right--;
                    }
                    right--;
                    }
                    else if(sum<target){
                        left++;
                    }
                    else{
                        right--;
                    }
                   
                }
            }
        }
        return results;
    }
};

时间复杂度：$O(n^3)$，其中n是数组的长度。排序的时间复杂度为$O（nlogn）$，枚举四元组的时间复杂度为$O(n^3)$,因此总的时间复杂度为$O（n^3+nlogn）=O(n^3)$

空间复杂度：$O（1）$，忽略返回值和排序的栈开销，仅用到若干变量。

24. 560 和为k的子数组

解法一：前缀和+哈希表

假设nums数组中[j,i]组成的子数组的和为k(j<=i)，首先定义前缀和pre[i]表示[0…i]里所有数的和，则pre[i]可以由pre[i-1]递推而来：

$$pre[i]=pre[i?1]+nums[i]$$

那么如果[j,…,i]的这个子数组的和为k,其实等价于在前缀和数组中

$$pre[i]?pre[j?1]==k$$

即：$pre[j?1]==pre[i]?k$

所以我们考虑以 i结尾的和为 k 的连续子数组个数时只要统计有多少个前缀和为pre[i]?k 的 pre[j] 即可。我们建立哈希表 prefixSumCount以和为键，出现次数为对应的值，记录 pre[i] 出现的次数，从左往右边更新prefixSumCount 边计算答案，那么以 i 结尾的答案prefixSumCount[pre[i]?k] 即可在 O(1) 时间内得到。最后的答案即为所有下标结尾的和为 k 的子数组个数之和。

需要注意的是，从左往右边更新边计算的时候已经保证了prefixSumCount[pre[i]?k] 里记录的 pre[j] 的下标范围是 0≤j≤i 。同时，由于pre[i] 的计算只与前一项的答案有关，因此我们可以不用建立 pre 数组，直接用 pre 变量来记录 pre[i?1] 的答案即可。

代码：

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int,int>prefixSumCount;
        int count=0;
        int pre=0;
        //初始化，表示前缀和为0的个数为1
        prefixSumCount[0]=1;
        for(int i=0;i<nums.size();i++){
            pre+=nums[i];
            //查看是否存在前缀和为pre-k，如果存在，说明找到了一个i结尾的，和为k的子数组
            if(prefixSumCount.find(pre-k)!=prefixSumCount.end()){
                count+=prefixSumCount[pre-k];
            }
            prefixSumCount[pre]++;
        }
        return count;
    }
};

时间复杂度：O(n) 其中 n 为数组的长度。我们遍历数组的时间复杂度为O(n)，中间利用哈希表查询删除的复杂度均为O(1)，因此总时间复杂度为 O(n)。

空间复杂度：O(n) 其中 n为数组的长度。哈希表在最坏情况下可能有 n个不同的键值，因此需要 O(n) 的空间复杂度。

解法二：枚举，方法通过重循环遍历得到以索引位置为i结尾的连续子数组的个数和，其中[j…i]的这个子数组的和恰好为k。详细见官方题解：

560. 和为 K 的子数组 - 力扣（LeetCode）

25. 523 连续的子数组和

解法：

这是一道很经典的前缀和题目。
数据范围为 $10^4$ ，因此无论是纯朴素的做法 $O(n^3)$,还是简单使用前缀和优化的做法$O(n^2)$都不能满足要求。

我们需要从 k的倍数作为切入点来做。

预处理前缀和数组 pre，方便快速求得某一段区间的和。然后假定[i,j] 是我们的目标区间，那么有：

$pre[j]?pre[i?1]=n?k$

经过简单的变形可得：

$\frac{pre[j]}{k}?\frac{pre[i?1]}{k}=n$
要使得两者除 k相减为整数，需要满足pre[j] 和 [i?1] 对 k取余相同。

也就是说，我们只需要枚举右端点 j，然后在枚举右端点 j 的时候检查之前是否出现过左端点 i，使得 pre[j] 和pre[i?1] 对 k 取余相同。

代码：

class Solution {
public:
    bool checkSubarraySum(vector<int>& nums, int k) {
        int n=nums.size();
        unordered_set<int>set;
        if(n<2)
        return false;
        vector<int>pre(n+1);
        for(int i=1;i<=n;i++){
            pre[i]=pre[i-1]+nums[i-1];
        }
        for(int i=2;i<=n;i++){
            set.insert(pre[i-2]%k);
            if(set.count(pre[i]%k))
             return true;
        }
        return false;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

26. 525 连续数组

解法：前缀和 + 哈希表
由于「0 和 1 的数量相同」等价于「1 的数量减去 0 的数量等于 0」，我们可以将数组中的 0 视作 ?1，则原问题转换成「求最长的连续子数组，其元素和为 0」。

因此，当我们遇到 0 时，将其视为 -1，遇到 1 时，保持为 1。然后，我们用一个变量 preSum 来记录当前位置的累积和。如果在两个位置 i 和 j（i < j）处 preSum，那么说明从位置 i 到位置 j 的子数组中 0 和 1 的数量相等。

1. 创建一个哈希表 sum2index用于存储累积和及其对应的索引。初始化时，累积和为 0 的索引为 -1。
2. 遍历数组，将 0 替换为 -1，计算累积和。
3. 如果 preSum 在 sum2index则更新最大长度为当前位置索引与 sum2index[preSum]` 之差。
4. 如果 preSum 在 sum2index 中不存在，则将当前位置的索引记录在 ``sum2index`中。
5. 返回最大长度作为结果。

下面是代码中的注释，帮助理解解题思路

代码：

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
    if(nums.size()<2)
    return 0;
    int maxlen=0;
    int preSum=0;
    unordered_map<int,int>sum2index;
    sum2index[0]=-1;
    for(int i=0;i<nums.size();i++){
        if(nums[i]==0)
        preSum--;
        else
        preSum++;
        if(sum2index.count(preSum)){
            maxlen=max(maxlen,i-sum2index[preSum]);
        }
        else{
            sum2index[preSum]=i;
        }
    }
    return maxlen;
    }
};

时间复杂度：O(n)，其中 n 是数组 nums 的长度。需要遍历数组一次。

空间复杂度：O(n)，其中 n 是数组nums 的长度。空间复杂度主要取决于哈希表，哈希表中存储的不同的preSum的值不会超过n个。