科研绘图（七）箱形图

箱形图（Boxplot）是一种用于图形化表示数据分布的统计图表。以下是对箱形图主要部分的详细介绍：

1. 中位数（Median）：

???- 箱形图中的一条线（通常是箱子中的一条线），表示数据集的中位数，也就是将数据集分成相等的上下两部分的值。

2. 四分位数（Quartiles）：

???- 第一四分位数（Q1/下四分位数）：位于箱子底部的线，表示所有数据中低于此值的占25%。

???- 第三四分位数（Q3/上四分位数）：位于箱子顶部的线，表示所有数据中高于此值的占25%。

???- 箱子（即Q1和Q3之间的区域）包含了中间50%的数据，称为四分位数范围（Interquartile Range, IQR）。

3. 须（Whiskers）：

???- 这些从箱体向外延伸的线条表示数据的变异性，它们延伸到箱形图外的最高点和最低点，但不包括异常值。须的长度一般是1.5倍的四分位数范围（IQR），用于判断异常值的标准。

4. 异常值（Outliers）：

???- 异常值通常用点表示，并且是那些低于Q1-1.5IQR或高于Q3+1.5IQR的数据点。这些点是数据中的异常值，可能是由于各种原因造成，如测量误差或数据输入错误。

5. "箱"体（Box）：

???- 箱体的边界由Q1和Q3确定，箱体的长度表示了数据集中值的散布程度，即四分位距。箱体越长，数据越分散。

6. 数据的分布：

???- 箱形图不仅可以显示数据的中心趋势，还可以显示数据的分布形态。例如，箱体对称表示数据较为均匀地分布在中位数的两侧；如果箱体偏向一侧，表明数据分布可能是偏斜的。

箱形图的优点在于它简洁地概括了数据的中心位置、散布和偏斜程度以及异常值。通过箱形图，我们可以迅速了解数据集的关键统计特性，并比较不同数据集的特点。例如，在医学研究中，箱形图可以用来展示不同治疗组的患者反应的差异；在商业分析中，它可以展示产品销售的季节性波动等。

箱形图也常常用于多个数据集的比较。比如，上面示例中的箱形图跨越多年份，可以用来比较不同年份的数据分布差异。每一年的数据分布情况都可以通过对应的箱形图直观展现，而年份之间的比较可以通过观察箱体的位置、大小和异常值的差异来进行。

值得注意的是，箱形图虽然提供了数据分布的可视化，但它不会显示数据分布的具体形状，如是否是双峰或是正态分布等。对于这些细节，通常需要配合直方图或核密度估计等其他统计图表来进一步分析。

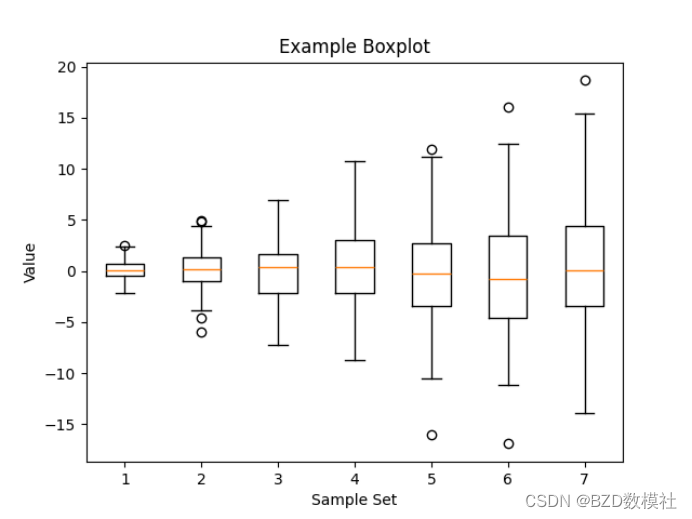
import matplotlib.pyplot as plt
import numpy as np

# Generate some example data
np.random.seed(10)
data = [np.random.normal(0, std, 100) for std in range(1, 8)]

# Create a boxplot
plt.boxplot(data)

plt.title('Example Boxplot')
plt.xlabel('Sample Set')
plt.ylabel('Value')

# Show the boxplot
plt.show()

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

# Use seaborn style for better aesthetics
sns.set(style="whitegrid")

# Generate some example data
np.random.seed(10)
data = [np.random.normal(0, std, 100) for std in range(1, 8)]

# Create a boxplot with additional styling
plt.figure(figsize=(12, 6))  # Set the figure size

# Define the properties for the boxplot elements
boxprops = dict(linestyle='-', linewidth=2, color='darkgoldenrod', facecolor='lightyellow')
medianprops = dict(linestyle='-', linewidth=2, color='firebrick')
whiskerprops = dict(linestyle='--', linewidth=2, color='darkorange')
capprops = dict(linestyle='-', linewidth=2, color='black')
flierprops = dict(marker='o', markerfacecolor='green', markersize=12, linestyle='none')
meanprops = dict(marker='D', markeredgecolor='black', markerfacecolor='blue', markersize=8)

# Creating the boxplot with customized properties
plt.boxplot(data, patch_artist=True, showmeans=True, boxprops=boxprops,
            medianprops=medianprops, whiskerprops=whiskerprops,
            capprops=capprops, flierprops=flierprops, meanprops=meanprops)

# Add titles and labels
plt.title('Enhanced Boxplot', fontsize=16, fontweight='bold')
plt.xlabel('Sample Set', fontsize=12)
plt.ylabel('Value', fontsize=12)

# Set the ticks and labels
plt.xticks(np.arange(1, len(data) + 1), [f'Set {i}' for i in range(1, len(data) + 1)], fontsize=10)
plt.yticks(fontsize=10)

# Show the boxplot with a tighter layout
plt.tight_layout()
plt.show()

?

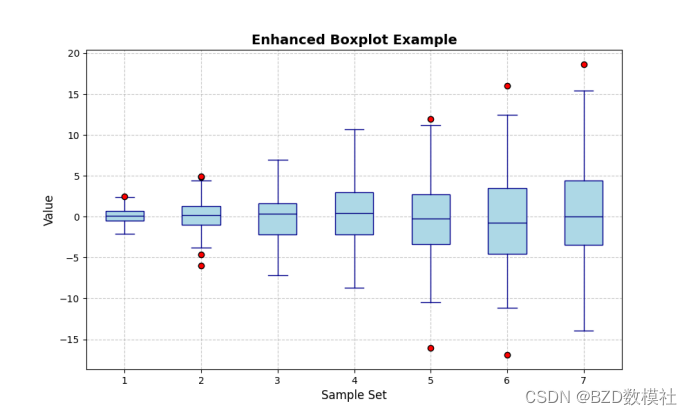
为了进一步美化可视化结果，对于颜色和样式：箱体填充了浅蓝色，边框和其他元素使用了深蓝色，中位数线为海军蓝色。对于异常值：用红色圆点标记，以突出显示。对于标题和标签：增加了标题和坐标轴标签的字体大小，并为标题添加了粗体样式。对于网格线：添加了虚线网格，透明度设为0.7，以便更好地阅读数据。

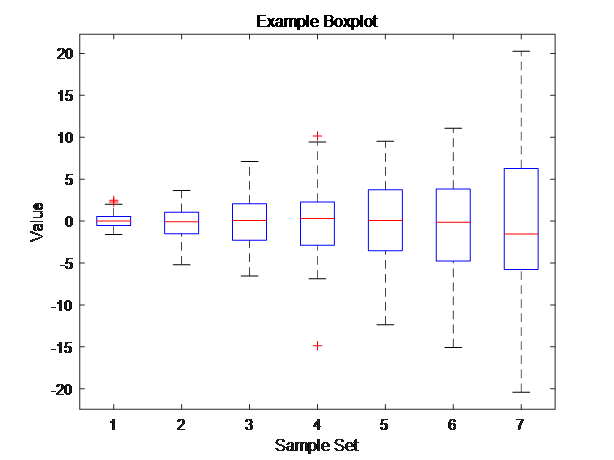
以下为matlab实现代码以及可视化结果

% 设置随机数种子
rng(10);

% 生成数据
data = {};
for std = 1:7
data{std} = normrnd(0, std, [100, 1]);
end

% 创建箱形图
boxplot(cell2mat(data))

% 设置图表标题和轴标签
title('Example Boxplot');
xlabel('Sample Set');
ylabel('Value');

% 显示图表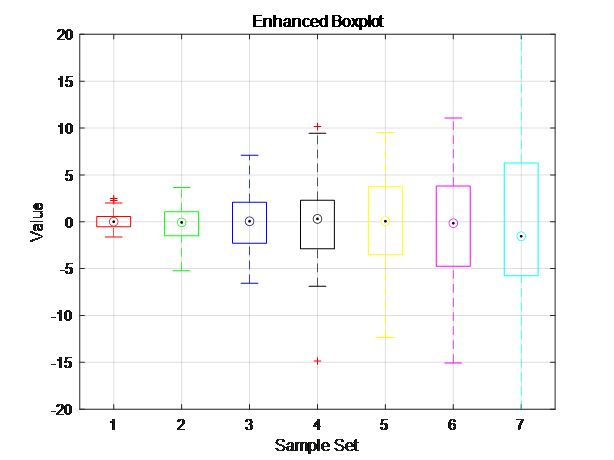

?

% 设置随机数种子
rng(10);

% 生成数据
data = {};
for std = 1:7
data{std} = normrnd(0, std, [100, 1]);
end

% 创建箱形图
boxplot(cell2mat(data), 'Colors', 'rgbkymc', 'MedianStyle', 'target', 'OutlierSize', 4)

% 设置图表标题和轴标签
title('Enhanced Boxplot');
xlabel('Sample Set');
ylabel('Value');

% 增加网格线
grid on;

% 调整坐标轴刻度和范围
ax = gca;
ax.XTick = 1:7;
ax.YLim = [-20, 20];

% 显示图表
进一步增强了箱形图的视觉效果，包括设置了背景色、为箱体添加了不透明度、自定义了离群点样式、改进了标题和轴标签的样式，以及设置了网格线的样式。大家可以根据自己的需求和喜好继续调整这些设置。

?进一步增强了箱形图的视觉效果，包括设置了背景色、为箱体添加了不透明度、自定义了离群点样式、改进了标题和轴标签的样式，以及设置了网格线的样式。大家可以根据自己的需求和喜好继续调整这些设置。

?

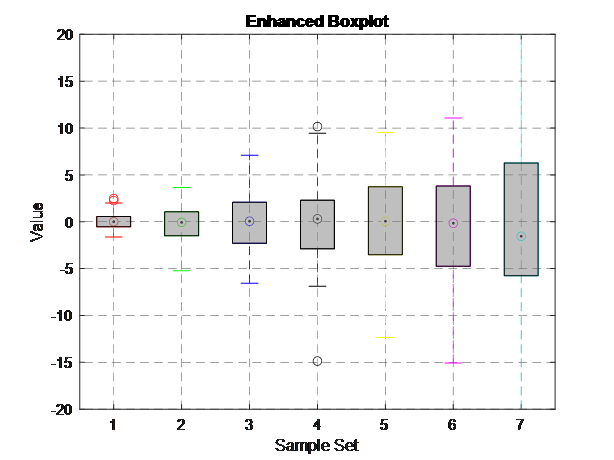箱形图作为数据可视化的工具，拥有一系列的优点和缺点：

?优点

1. 简洁性：

???- 箱形图以一种非常紧凑和信息密集的方式展示数据分布，使得对数据的中位数、四分位数和异常值一目了然。

2. 比较性：

???- 当需要在同一图表中比较多个数据集时，箱形图尤其有用。它可以轻松地并排放置，以便直观地比较不同数据集的中心趋势和分散程度。

3. 识别异常值：

???- 异常值可以清晰地表示出来，这对于异常值分析和异常检测非常重要。

4. 不受异常值影响：

???- 箱形图的构建方法（使用中位数和四分位数）使其对异常值不敏感，因此它们提供了一个稳健的数据分布视图。

5. 数据分布的非参数摘要：

???- 箱形图不假设数据的基础分布，这使得它们成为一种非参数的方法，即它们不依赖于数据的分布符合某个特定的数学形式。

?缺点

1. 数据分布细节：

???- 箱形图不显示数据的分布细节，例如是否对称、是否多峰或数据的确切分布形状。因此，可能需要额外的直方图或核密度估计图来获取这些信息。

2. 异常值的过度简化：

???- 尽管箱形图可以显示异常值，但它们不提供关于异常值数量或其分布的具体细节。此外，它也不区分远端和近端异常值。

3. 不显示每个数据点：

???- 箱形图不展示单个数据点（除了可能的异常值），这意味着数据的多样性和个体差异可能被隐藏。

4. 固定的异常值识别规则：

???- 异常值通常根据1.5*IQR的规则确定，这可能不适用于所有类型的数据集。对于有些数据集来说，这个规则可能过于严格或过于宽松。

5. 对于小样本数据的限制：

???- 当数据量较少时，箱形图可能不够精确，因为四分位数和异常值可能会受到个别数据点的过度影响，从而导致误导性的解释。

6. 潜在的误解：

???- 箱形图的读法不如其他一些图表直观，如条形图或折线图，可能需要用户有一定的统计知识才能正确解读。

7. 聚集效应：

???- 对于大数据集，许多实际值可能会聚集在四分位数，这使得箱形图看起来非常相似，难以区分。

总结来说，箱形图是一个非常强大的工具，尤其是在需要快速了解数据集的中心趋势、离散程度和异常值时。然而，由于它的一些局限性，通常最好将箱形图与其他数据分析工具结合使用，以获得对数据的全面理解。

?