【C语言】排序（三）（快速排序：递归与非递归实现）
发布时间：2023年12月29日
前言?
在本篇博客中，作者会带领你理解和实现快速排序，并且将会使用递归和非递归两种方式分别实现。
一.排序思想
快速排序的基本思想是：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
二.写代码流程及思路
绝大部分排序都可以分为单趟排序和多趟排序，当我们要写排序时，可以先写单趟排序，再写多趟排序，这样使得我们写代码简单易懂。?
?三.单趟快速排序
1.左右指针法
①选取数组中的最后一个数作为基准值key。
②定义左右指针left，right。left从头往右走，right从尾往左走。
③left指针往右找比key大的值，right指针往左找比key小的值。
④两个指针都找到后，交换两个指针所值的数。
⑤left，right指针继续找，重复③④步骤。
⑥当left和right相遇后，停止移动，并把right指向的值与key交换。
此时，已完成一趟快速排序。
并且key的左边都比key小，key的右边都比key大，并且key处在了正确的位置。
2.单趟快速排序流程图
3.单趟快速排序代码实现?
//一趟快速排序，左右指针法，其中begin为待排数组的第一个元素，end为数组的最后一个元素
int PartSort1(int* arr, int begin, int end)
{
int key = arr[end];//取最后一个数作为基准值key
int left = begin;//左指针起始位置
int right = end;//右指针起始位置
while (left < right)//当左指针在右指针的左边，即区间还有效
{
while (left < right && arr[left] <= key)//左指针往右找大
{
left++;
}
while (left < right && arr[right] >= key)//右指针往左找小
{
right--;
}
Swap(&arr[left], &arr[right]);//交换左右指针的值
}
Swap(&arr[left], &arr[end]);//将基准值key换到中间
return left;//返回中间的位置
}4.易错点分析
①.基准值如何取
????????一般来说找基准值key，要么找最左边，要么找最右边，
????????当找最左边的数为key时，需要right指针先动，left指针后动。
????????当找最右边的数为key时，需要left指针先动，right指针后动。
????????如果不按上面要求，则排序会出问题。
②left和right指针循环条件
while (left < right && arr[left] <= key)
while (left < right && arr[right] >= key)????????这两条循环语句中的后半段一定要有等号=，否则程序可能会出现死循环
????????原因：在待排的数组中，有两个与key值相同的数时，程序会陷入死循环。
????????如下序列：1,2,6,5,6,8,9,6?
③left和right指针的起始位置
int left = begin;//左指针起始位置
int right = end;//右指针起始位置????????左右指针的起始位置一定要从begin和end开始：
????????有的人可能认为既然arr[end]作为key，那么我的right指针是不是可以从end-1开始，答案是不行的。当待排区间完全逆序或者有序时，程序的结果会不正确。?
?四.多趟快速排序
当一趟快速排序完成后，数组可以分为三个部分，分别是
[begin,div-1]? ? ?div? ? ?[div+1,end]?
?
这个时候[begin,div-1] 和?[div+1,end]?是无序的，div是有序的，所以下一步只需令
[begin,div-1] 和?[div+1,end]和有序即可，即下一步对这两块区间排序即可。
1.多趟快速排序代码实现?
void QuickSort(int* arr, int begin,int end)//快速排序递归实现
{
if (begin >= end)//当待排区间不合法时，返回
{
return;
}
int div = PartSort1(arr, begin, end);
//一趟快速排序完成后分为三个区间[begin,div-1] div [div+1,end] div为已经排完的位置，后面只需要排[begin,div-1] 和 [div+1,end]区间即可
QuickSort(arr, begin, div - 1);//排[begin,div-1]区间
QuickSort(arr, div + 1, end);//排[div+1,end]区间
}快速排序递归图解：?
理想情况下，我们可以假设每一次排序都可以把基准值key移动到中间位置，所得到的递归图解如下。
五.单趟快速排序多种方法
在单趟快速排序中，不仅有左右指针法，还有挖坑法和前后指针法，下面对这两种方法做简单介绍和实现。?
1.挖坑法
将选取基准值key的位置作为坑位，left指针往右找大放入坑位中，right指针往左找小放入坑位中，每一次填坑都会形成新坑位。?
①挖坑法代码实现
int PartSort2(int* arr, int begin, int end)
{
int key = arr[end];//选最后一个元素作为基准值key
int left = begin;//左指针指向第一个元素
int right = end;//右指针指向最后一个元素
while (left < right)
{
while (left < right && arr[left] <= key)//左指针往右找大填坑
{
left++;
}
arr[right] = arr[left];
while (left < right && arr[right] >= key)//右指针往右找小填坑
{
right--;
}
arr[left] = arr[right];
}
arr[left] = key;
return left;
}2.前后指针法
后指针往后找小的值，找到后，前指针++，再交换前后指针。?
?①前后指针法代码实现
int PartSort3(int* arr, int begin, int end)//前后指针法
{
int key = arr[end];
int prev = begin - 1;//前指针
int tail = begin;//后指针
while (tail < end)
{
if (arr[tail] < key)
{
prev++;
Swap(&arr[prev], &arr[tail]);
}
tail++;
}
prev++;
Swap(&arr[prev], &arr[tail]);
return prev;
}六.优化?
1.时间复杂度分析
时间复杂度是看最坏的情况，然而现在的快速排序代码的时间复杂度为O（n2）。?
原因：当数组已经有序或逆序的时候，就会出现最坏的情况。
理想情况下，如下图所示，每次排完一次后，div处在一个二分的位置。
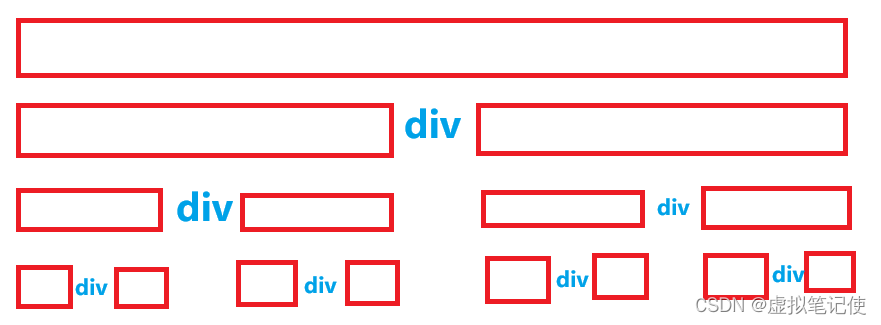?最坏情况如下图所示，?每次排完一次后，div都正好是处在最后一个位置，这是因为数组原本就已经有序导致的。所以这个时候我们需要对代码进行优化。
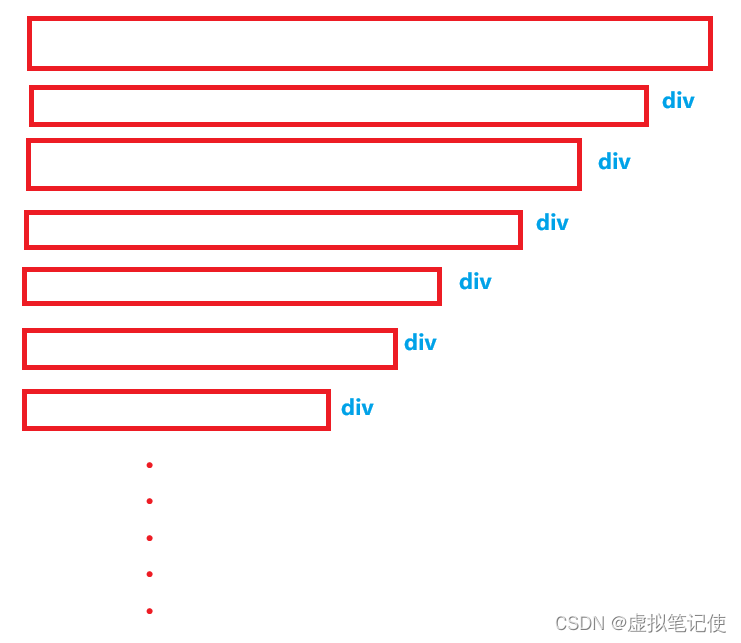
2.优化方法（三数取中法）
在我们选取key值时，先在数组的begin、end和（end-begin）/2的位置中选取一个中间值，并把这个中间值换到end的位置。?此时一趟排完后，div处在二分的位置，达到理想情况。
?①三数取中代码实现
//用于快速排序 的 三数取中（即在begin、end和 (begin+end)/2之间取一个处在中间的值，这样保证在一趟排序中，key值不会是最大，也不会是最小
int GetMidIndex(int* arr, int begin, int end)
{
assert(arr);
int mid = (begin + end) / 2;
//如果arr[begin]最大，则在mid和end中选最大
if (arr[begin] > arr[mid])
{
if (arr[begin] > arr[end])
{
return arr[mid] > arr[end] ? mid : end;
}
}
//如果arr[mid]最大，则在begin和end中选最大
else if (arr[mid] > arr[end])
{
if (arr[mid] > arr[begin])
{
return arr[end] > arr[begin] ? end : begin;
}
}
//如果arr[end]最大，则在begin和mid中选最大
else
{
return arr[begin] > arr[mid] ? begin : mid;
}
//返回的是 中间的数 的下标
}3.优化后的快速排序代码实现（这里选取左右指针法为例）?
//用于快速排序 的 三数取中（即在begin、end和 (begin+end)/2之间取一个处在中间的值，这样保证在一趟排序中，key值不会是最大，也不会是最小
int GetMidIndex(int* arr, int begin, int end)
{
int mid = (begin + end) / 2;
if (arr[begin] > arr[mid])
{
if (arr[begin] > arr[end])
{
return arr[mid] > arr[end] ? mid : end;
}
}
else if (arr[mid] > arr[end])
{
if (arr[mid] > arr[begin])
{
return arr[end] > arr[begin] ? end : begin;
}
}
else
{
return arr[begin] > arr[mid] ? begin : mid;
}
//返回的是 中间的数 的下标
}
//一趟快速排序，左右指针法，其中begin为待排数组的第一个元素，end为数组的最后一个元素
int PartSort1(int* arr, int begin, int end)
{
int mid = GetMidIndex(arr, begin, end);//三数取中优化代码
Swap(&arr[mid], &arr[end]);
int key = arr[end];//取最后一个数作为基准值key
int left = begin;//左指针起始位置
int right = end;//右指针起始位置
while (left < right)//当左指针在右指针的左边，即区间还有效
{
while (left < right && arr[left] <= key)//左指针往右找大
{
left++;
}
while (left < right && arr[right] >= key)//右指针往左找小
{
right--;
}
Swap(&arr[left], &arr[right]);//交换左右指针的值
}
Swap(&arr[left], &arr[end]);//将基准值key换到中间
return left;//返回中间的位置
}4.利用直接插入排序优化
实际上在C语言库函数里面，有一个快排函数qsort，这个库函数里面还做了优化，就是当待排区间的数小于10个时，对这个区间不再进行快速排序，而是使用了直接插入排序来对这组数排序，原因是，当待排的数较少时，快速排序的性能并不比直接插入排序好，所以才加了这层优化，这里博主不再演示，有兴趣的朋友可以自己修改代码优化，另外附上直接插入排序详解。【C语言】排序（一）（直接插入排序、希尔排序）-CSDN博客
七.非递归实现?
1.实现流程图和解释
在快速排序的非递归实现中，通常用栈来完成，主要是利用了栈的后进先出的特点。
具体实现入下图：
先对总区间入栈，入完栈后，取出区间给left和right，只对[left,right]进行一趟快速排序，排完一趟后，会得到一个div值，继续对div的左区间和右区间入栈，后继续出栈，对[left，right]进行排序，以此类推。?
2. 非递归代码实现
void QuickSortNonR(int* arr, int begin, int end)//快速排序非递归实现
{
int Stack[20] = { 0 };//创建一个栈区
int size = 0;//栈区中的元素个数，同时能作为下标来用
//将区间[begin,end]入栈，注意！！！ 先入右边，再入左边
Stack[size] = end;
size++;
Stack[size] = begin;
size++;
//当栈不为空时
while (size > 0)
{
//将左右出栈
int left = Stack[size - 1];
size--;
int right = Stack[size - 1];
size--;
if (left < right)
{
int div = PartSort1(arr, left, right);
//一趟排完后，区间分为[left,div-1] div [div+1,right]
//将[left,div-1] [div+1,right]入栈
Stack[size] = right;
size++;
Stack[size] = div + 1;
size++;
Stack[size] = div - 1;
size++;
Stack[size] = left;
size++;
}
}
}八.时间复杂度和空间复杂度
快速排序的时间复杂度为O（n*logN）
空间复杂度为O（logN） （因为递归会创建函数栈帧空间）
九.稳定性分析
什么是稳定性？
稳定性是，如果一组数里面有两个相同的数，则排序完成后，如果不会改变他们的相对顺序，则这个排序算法是稳定的，否则是不稳定的。
结论
快速排序是不稳定的。?
十.所有源代码
#include<stdio.h>
void Swap(int* num1, int* num2)//用于交换数组中的两个数
{
int tmp = *num1;
*num1 = *num2;
*num2 = tmp;
}
void Print(int* arr, int sz)
{
for (int i = 0; i < sz; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
//用于快速排序 的 三数取中（即在begin、end和 (begin+end)/2之间取一个处在中间的值，这样保证在一趟排序中，key值不会是最大，也不会是最小
int GetMidIndex(int* arr, int begin, int end)
{
int mid = (begin + end) / 2;
if (arr[begin] > arr[mid])
{
if (arr[begin] > arr[end])
{
return arr[mid] > arr[end] ? mid : end;
}
}
else if (arr[mid] > arr[end])
{
if (arr[mid] > arr[begin])
{
return arr[end] > arr[begin] ? end : begin;
}
}
else
{
return arr[begin] > arr[mid] ? begin : mid;
}
//返回的是 中间的数 的下标
}
//一趟快速排序，左右指针法，其中begin为待排数组的第一个元素，end为数组的最后一个元素
int PartSort1(int* arr, int begin, int end)
{
int mid = GetMidIndex(arr, begin, end);
Swap(&arr[mid], &arr[end]);
int key = arr[end];//取最后一个数作为基准值key
int left = begin;//左指针起始位置
int right = end;//右指针起始位置
while (left < right)//当左指针在右指针的左边，即区间还有效
{
while (left < right && arr[left] <= key)//左指针往右找大
{
left++;
}
while (left < right && arr[right] >= key)//右指针往左找小
{
right--;
}
Swap(&arr[left], &arr[right]);//交换左右指针的值
}
Swap(&arr[left], &arr[end]);//将基准值key换到中间
return left;//返回中间的位置
}
int PartSort2(int* arr, int begin, int end)//挖坑法
{
int key = arr[end];//选最后一个元素作为基准值key
int left = begin;//左指针指向第一个元素
int right = end;//右指针指向最后一个元素
while (left < right)
{
while (left < right && arr[left] <= key)//左指针往右找大填坑
{
left++;
}
arr[right] = arr[left];
while (left < right && arr[right] >= key)//右指针往右找小填坑
{
right--;
}
arr[left] = arr[right];
}
arr[left] = key;
return left;
}
int PartSort3(int* arr, int begin, int end)//前后指针法
{
int key = arr[end];
int prev = begin - 1;//前指针
int tail = begin;//后指针
while (tail < end)
{
if (arr[tail] < key)
{
prev++;
Swap(&arr[prev], &arr[tail]);
}
tail++;
}
prev++;
Swap(&arr[prev], &arr[tail]);
return prev;
}
void QuickSort(int* arr, int begin,int end)//快速排序递归实现
{
if (begin >= end)//当待排区间不合法时，返回
{
return;
}
int div = PartSort1(arr, begin, end);
//一趟快速排序完成后[begin,div-1] div [div+1,end] div为已经排完的位置，后面只需要排[begin,div-1] 和 [div+1,end]区间即可
//Print(arr, end - begin + 1);
QuickSort(arr, begin, div - 1);//排[begin,div-1]区间
QuickSort(arr, div + 1, end);//排[div+1,end]区间
}
void QuickSortNonR(int* arr, int begin, int end)//快速排序非递归实现
{
int Stack[20] = { 0 };//创建一个栈区
int size = 0;//栈区中的元素个数，同时能作为下标来用
//将区间[begin,end]入栈，注意！！！ 先入右边，再入左边
Stack[size] = end;
size++;
Stack[size] = begin;
size++;
//当栈不为空时
while (size > 0)
{
//将左右出栈
int left = Stack[size - 1];
size--;
int right = Stack[size - 1];
size--;
if (left < right)
{
int div = PartSort1(arr, left, right);
//一趟排完后，区间分为[left,div-1] div [div+1,right]
//将[left,div-1] [div+1,right]入栈
Stack[size] = right;
size++;
Stack[size] = div + 1;
size++;
Stack[size] = div - 1;
size++;
Stack[size] = left;
size++;
}
}
}
int main()
{
int arr1[] = { 4,5,8,6,2,1,596,14,6 };
int arr2[] = { 48,45,1,23,60,14 };
Print(arr1, sizeof(arr1) / sizeof(int));
QuickSort(arr1, 0, sizeof(arr1) / sizeof(int) - 1);
Print(arr1, sizeof(arr1) / sizeof(int));
Print(arr2, sizeof(arr2) / sizeof(int));
QuickSortNonR(arr2, 0, sizeof(arr2) / sizeof(int) - 1);
Print(arr2, sizeof(arr2) / sizeof(int));
return 0;
}
文章来源:https://blog.csdn.net/EWIAW_ilove/article/details/135211176
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 并行开发模式:低代码缩短产品开发周期,实现跨部门高效协作
- 科普贴：通过10个要点来快速认识了解Vue.js前端框架
- python的介绍，带入，安装
- Linux命令之 systemctl 指令
- 常用的几种包管理器 npm yarn cnpm pnpm 安装
- 鸿蒙开发之地理位置
- 数据库开发之内连接和外连接的详细解析
- 分布式核心技术之分布式共识
- vite配置别名时遇到错误Error: Dynamic require of “path“ is not supported
- Flink系列之：背压下的检查点